До недавнего времени формирование программ воспроизводства жилищного фонда посредством проведения его капитального ремонта осуществлялось на основе применения сетевых моделей, которые основывались на поточных методах выполнения ремонтных работ и позволяли рассчитывать планы их проведения по каждому типу объектов. Одним из существенных недостатков применения этих моделей являются завышенные требования к точности расчетов, вследствие чего возникала необходимость обработки значительных объемов информации, большая часть которой, в конечном счете, оказывалась избыточной. Кроме того, сетевые модели не позволяли учитывать существенные ограничения в расчетах, накладываемые различными сроками поступления средств, различными источниками финансирования, а так же их варьирования по объемам. В результате затраты времени и усилия на разработку точных планов перестали себя оправдывать, поскольку на практике только что разработанный план через короткий промежуток времени нуждался в проведении разного рода корректировок и новом перерасчете.

Для устранения отмеченных недостатков предлагается новый подход к реализации программ воспроизводства жилищного фонда, который обеспечивает эффективные результаты как с позиций затрачиваемого времени, так и с точки зрения оптимизации ресурсного, прежде всего финансового, обеспечения. В основу этого подхода положено распределение работ между объектами программы не по времени, а по объемам, что более точно отражает зависимость между смежными работами и не требует предварительных расчетов продолжительности работ. Для нахождения оптимального варианта набора работ, проведение которых обеспечит реализацию выделенного объема финансовых ресурсов, используется математический аппарат методологии эволюционных вычислений (генетических алгоритмов), позволяющей наиболее эффективно решать задачи поиска глобального экстремума для сложной системы с учетом всей совокупности финансовых ограничений [2, 3]. Такой подход позволяет повысить чувствительность модели к ограничениям по ресурсам и уйти от использования жестких сетевых моделей.

В процессе работы генетического алгоритма многократно применяются операторы отбора, скрещивания, мутации и редукции. Поскольку операторы по своей сути направлены на улучшение каждой отдельной особи (работы), то под их воздействием происходит постепенное улучшение популяции (плана работ) в целом [1, с.9]. Это обстоятельство является одним из важнейших преимуществ, определивших выбор генетических алгоритмов в качестве методологической основы решения рассматриваемой нами задачи.

Основным ограничением при формировании программ воспроизводства жилищного фонда является объем финансирования. Этот показатель определяется как суммарная величина инвестиций собственников жилья, а так же средств бюджетов всех уровней (федерального, регионального, местного), которые в условиях мирового экономического и финансового кризиса, скорее всего, будут рассчитываться как некие значения лимитов. Поэтому необходимо определить такую последовательность реализации программы воспроизводства жилищного фонда, чтобы за один период финансирования (календарный год) был выполнен максимальный объем работ пропорциональный общей сумме финансирования с учетом ограничений по его объему. Не достижение этого приведет, с одной стороны, к неполному использованию средств бюджетов разного уровня и других источников финансирования, а с другой – к снижению ожидаемого социального эффекта от реализации программы.

Для учёта конструктивных особенностей включенных в программу объектов, сгруппируем всё множество многоквартирных жилых домов (МКД) в m типов и обозначим номер типа индексом i. Каждый тип здания характеризуется определённым набором конструктивных элементов. Номер конструктивного элемента обозначим через j. Общее количество конструктивных элементов у здания категории i обозначим через n_i. Приняв, что формирование программы воспроизводства жилищного фонда ведётся на временном периоде длительностью Т, обозначим за y_kijt вид работ по капитальному ремонту j-го конструктивного элемента k-го здания, относящегося к категории i, в момент времени t; , ,  t =  0, …, T-1.

В качестве исходных данных для решения задачи формирования программы воспроизводства жилищного фонда используются ряды последовательных оценок для каждого вида работ по капитальному ремонту конструктивных элементов , полученные в результате обследования жилищного фонда: ориентировочная продолжительность ремонтных работ , объём финансовых затрат , расчетный экономический эффект , где j – тип конструктивного элемента, i – тип здания (см. табл.1).

Таблица 1

Технико-экономические зависимости для здания i-й категории

Решение задачи построения плана ремонтных работ ведётся в дискретном времени. Номер отрезка времени обозначим индексом t =  0, …, T, где Т – длительность планового периода.

Для обеспечения объектной и временной привязок ремонтных работ представим перспективный план в виде множества временных диаграмм, каждая из которых соответствует одному виду работ. Диаграммы разбиты на Т отрезков, соответствующих моментам времени t =  0, …, T, в качестве которых могут выступать неделя, декада, месяц, квартал. Каждой ячейке временной диаграммы ставится в соответствие булева величина , принимающая значение 1, если запланирован ремонт j-го конструктивного элемента k-го здания i-й категории, в момент времени t и 0 в остальных случаях. Совокупность переменных  определяет план работ. Таким образом, экономический эффект и затраты при выполнении ремонтной работы j-го элемента k-го здания i-й категории в момент времени t определяются произведениями x_kijt´e_kijt и x_kijt´c_kijt соответственно.

Экономический эффект S используется в качестве целевой функции:

.                                    (1)

Ограничение на объём финансовых ресурсов запишем в виде:

,                                                                   (2)

где С – максимальный (установленный) объём финансирования.

Предельно допустимое значение физического износа определяется предварительно заданными константами: 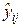, , . Если фактическое значение физического износа отдельного конструктивного элемента оказывается меньше этой величины, то он может быть включен в программу.

В результате ремонта значение физического износа уменьшается до величины, определяемой функцией неустранимого износа . Изменённый в результате ремонта физический износ обозначим , тогда условие безаварийности записывается в виде:

.                                                                  (3)

Ограничение на количество одновременно проводимых работ:

,                                                           (4)

где    ,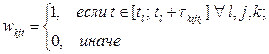

 – время начала l-го вида ремонтных работ по j-му конструктивному элементу k-го здания (многоквартирного жилого дома).

Это ограничение устанавливается опытным путем, исходя из возможности привлечения подрядных и субподрядных организаций к выполнению определенных видов работ на основании заключенных договоров подряда.

Ограничение на начало ремонтных работ, исключающее выход процесса ремонта за границы периода планирования Т:

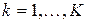,, ,          (5)

На переменные x_kijt также налагаются ограничения, связанные с определенной последовательностью выполнения отдельных видов работ. Начальным условием выполнения отдельных видов работ на объекте будет невозможность начала последующей работы до тех пор, пока не закончена определенная часть предыдущей работы. Общая продолжительность выполнения работы определяется величиной t_kijt. Для определения части предыдущей работы, по завершении которой становится возможным выполнение последующей работы используются коэффициенты совмещения работ по началу (К_Н) и по окончанию (К_О). Величина коэффициентов совмещения определяется пользователем, исходя из технологических особенностей каждого вида работ по капитальному ремонту.

Обозначим  – время начала l-й работы.

,               (6)

Ремонтная работа конструктивного элемента здания не должна проводиться параллельно с работой, имеющей индекс 0.

                    (7)

В случае невозможности выполнить ограничение безаварийности (3) целесообразно преобразовать его в критерий оптимальности, минимизирующий наибольший (8) или средний (9) ожидаемый износ на протяжении периода планирования:

,                                  (8)

.                                      (9)

Общая схема формирования программы капитального ремонта жилищного фонда включает 2 этапа:

1) получение допустимого решения с использованием критерия локальной оптимальности;

2) проведение оптимизации допустимого решения при помощи генетического алгоритма.

Целью первого этапа является поиск допустимого варианта решения задачи  близкого к оптимальному при условии выполнения ограничений. Алгоритм получения допустимого варианта решения задачи предусматривает, что первоначально все переменные  равны 0. Это означает, что ни одна работа не запланирована. На каждом шаге алгоритм присваивает одной из переменных значение 1 (заносит в план одну работу на момент времени t для j-го конструктивного элемента k-го здания, i-й категории) в соответствии с критерием локальной оптимальности и ограничениями. Для вычисления критерия локальной оптимальности используются ряды оценок затрат и эффекта:

h_kijt = e_kijt : c_kijt                                                                         (10)

В ячейку плана, соответствующую максимальному значению критерия, в соответствии с ограничениями заносится 1. Последовательность описанных шагов повторяется до тех пор, пока не будут исчерпаны финансовые средства C.

Полученное на первом этапе решение используется в качестве начального в алгоритме оптимизации допустимого варианта программы воспроизводства жилищного фонда с применением генетических алгоритмов на втором этапе. В качестве исходных данных (начальной популяции) используются расчетные значения сметной стоимости c_kijt, соответствующие каждой позиции вектора, то есть каждому блоку ремонтных работ. Тогда исходным решением нашей задачи в формализованном виде для варианта m будет ограничение на объём финансовых ресурсов (2), которое можно записать следующим образом:

C^m =                                                  (11),

где  - вероятность воспроизведения вида работ (его реализации в рамках программы) с учетом установленных исходных значений сметной стоимости, которая определяется по формуле:

                                                                (12)

Поскольку основные характеристики ремонтных работ не претерпевают изменений, то условие (11) можно представить в таком виде

C^m = = (c, p^m)                                                          (13)

В формуле (13) запись (c, p^m) означает скалярное произведение вектора c = { c_kijt } на вектор p^m = {}, а проекции вектора  принимают значения 0 или 1.  Таким образом, формула (13) описывает значение целевой функции, для которой необходимо найти максимум при ограничении вида

SC^m £ C                                                                                         (14),

где C – объем средств, выделенных для реализации программы.

Первым шагом применения генетического алгоритма является поиск в исходной популяции (программе воспроизводства жилищного фонда) потенциальных решений (наборов ремонтных работ) размером Q, который реализуется посредством генерации случайных выборок из нулей и единиц с последующим отбором элементов (видов работ), удовлетворяющих условию (14). Отбор осуществляет оператор на основе максимальных расчетных значений показателя вероятности воспроизведения видов работ (их реализации в рамках программы) с учетом установленных исходных значений сметной стоимости их выполнения. В результате становится возможным отсортировать исходную популяцию видов работ на объектах программы по вероятности их потенциальной реализации. Исходя из формулы (2), будет естественным предположить, что наибольшими значениями этого показателя будут обладать виды работ с максимальной сметной стоимостью.

Следующим шагом работы генетического алгоритма является создание новой популяции при помощи использования стандартных операторов скрещивания и мутации осуществляется выбор наиболее эффективных элементов (имеющих наибольшие значения расчетного показателя вероятности воспроизведения).

В результате многократного применения операторов отбора, скрещивания и мутации происходит формирование нового поколения – оптимального варианта реализации программы.

Шаг алгоритма завершается объявлением нового поколения текущим и его проверкой на выполнение критерия оптимальности.

Описанная последовательность будет повторяться до тех пор, пока на одном из потомков исходной популяции (программы воспроизводства жилищного фонда) не будет достигнуто условие SC^m = C. Если это условие не достигнуто, а число итераций не превышает предельно допустимого значения I_max (обычно устанавливается перед началом расчетов), то из всех полученных вариантов снова отбираются Q лучших по показателю новой расчетной вероятности воспроизведения и процесс повторяется, начиная с сопоставления вероятности воспроизведения.

Алгоритм формирования и оптимизации программы воспроизводства жилищного фонда в любом случае будет конечным, поскольку расчеты заканчиваются либо в случае достижения абсолютного результата (SC^m = C), либо в случае достижения установленного значения предельно допустимого числа итераций I_max.

В ходе проведенных исследований нами установлено, что использование генетических алгоритмов для формирования программ воспроизводства жилищного фонда позволяет не только находить решение оптимизационных задач большой размерности и проводить сами расчеты при изменении значений исходных параметров, но и учитывать различные изменения существующих ограничений. Применение генетических алгоритмов позволяет легко видоизменять и дополнять решение оптимизационной задачи при помощи операторов отбора, скрещивания и мутации. Таким образом, применение генетических алгоритмов оправдано не только на этапе формирования программы капитального ремонта жилищного фонда, но и при ее непосредственной реализации, поскольку обеспечивает поиск наиболее эффективных вариантов ее реализации при изменении целевых объемов финансирования или значений ограничений по ресурсам.

Исследование выполнено при финансовой поддержке Российского гуманитарного научного фонда, проект №10-02-00244а «Разработка организационно-экономических механизмов воспроизводства жилищного фонда в условиях кризиса».

Список литературы:

1. Еремеев А.В. Генетические алгоритмы и оптимизация. Учебное пособие. [Текст] / А.В. Еремеев.  – Омск: ОмГУ, 2008. – 23с.

2. Панченко Т.В. Генетические алгоритмы. Под ред. Ю.Ю. Тарасевича. [Текст] / Т.В. Панченко.  – Астрахань: ИД «Астраханский университет», 2007. – 87с.

3. Goldberg D.E. The Design of Innovation: Lessons from and for Competent Genetic Algorithms [Текст] / D.E. Goldberg // Kluwer Academic Publishers, Boston, MA 2002.