Статья опубликована в рамках: IX Международной научно-практической конференции «Экономика и современный менеджмент: теория и практика» (Россия, г. Новосибирск, 23 января 2012 г.)
Наука: Экономика
Секция: Теория управления экономическими системами
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
РЕШЕНИЕ ЗАДАЧ УПРАВЛЕНИЯ С ИСПОЛЬЗОВАНИЕМ КОМПЛЕКСНОГО МЕТОДА РАСЧЕТА СЕТЕВЫХ МОДЕЛЕЙ
Мандыч Ирина Александровна
ст. преподаватель МИТХТ, г. Москва
E-mail: MandychIA@pochta.ru
Сухорукова Светлана Михайловна
д-р. экон. наук, профессор МИТХТ, г. Москва
E-mail: sukhorukova@inbox.ru
В графической сетевой модели могут возникать разные по постановке задачи: определение максимального — критического среди всех возможных пути между некоторыми событиями, ранних и поздних сроков свершения всех событий, сроков начала и окончания работ; экономически оптимального сочетания процессов производства и управления в цепочке формирования ценностей в хозяйственной деятельности предприятий; минимального с экономической точки зрения пути между событиями; деятельности предприятия с минимальным суммарным риском и т. п. Все эти задачи позволяет решать универсальный комплексный метод, использующий при формулировании модели понятия оптимального программирования, сетевого планирования, решение задач в условиях неопределенности, теорию игр [3, c. 118]. Комбинируя варианты определения целевой функции и виды ограничений, метод позволяет решать многоцелевые задачи, задачи с несколькими исходными событиями, получать минимальные или максимальные общие и локальные результаты в статике и динамике [1, с. 477]. В зависимости от конкретики задачи, переменными параметрами в таких задачах могут быть как время, так и финансовые показатели, риски, вероятности, показатели экологичности, ресурсы и т. п. [2, с. 116]
Рассмотрим задачу на минимум пути.
Например, для задачи нахождения оптимального пути транспортировки (рисунок 1):
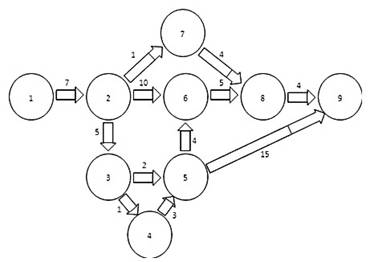
Рисунок 1. Модель расчета условного сетевого графика.
В этой модели целевой функцией будет завершающее событие (в терминологии сетевого планирования) или граф, максимум которого определяется, F= хn→ mах; ограничения модели составляют неравенства для каждого события xi, которые имеют вид: xj≤xi+tij.
F= хn→ max
х9≤x8+t89;
х9≤x5+t59;
х8≤x7+t78;
х8≤x6+t68;
х7≤x2+t27;
х6≤x5+t56;
х6≤x2+t26;
х5≤x4+t45;
х5<=x3+t35;
х4≤x3+t34;
х3≤x2+t23;
х2≤x1+t12.
На рисунке 2 показано решение в среде MS EXCEL, c использованием программной надстройки «ПОИСК РЕШЕНИЯ».
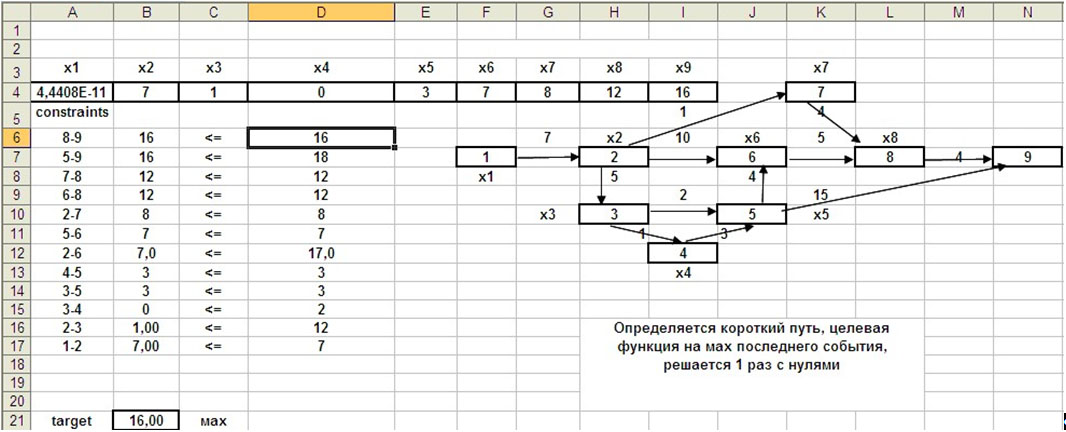
Рисунок 2. Решение задачи на минимум пути.
В решении определяются не только значения событий, которые составляют минимальный требуемый путь, но и значения событий, не определяющих минимальный путь, но показывающие те значения, которые должны были бы иметь события, чтобы минимальный путь проходил через них — это как бы ориентир для событий.
В модель могут быть включены дополнительные ограничения, лимитирующие некоторые параметры событий или работ, что часто бывает при участии в системе различных заинтересованных участников со своими условиями функционирования.
Необходимо отметить, что при решении с использованием EXEL все переменные надо исходно обнулить.
Данная модель может использоваться для решения не только для задач с одним завершающим событием и одним начальным событием, но и с большим их количеством. Примером задачи с несколькими исходными событиями и одним завершающим будет предыдущая модель, если убрать ограничение х3≤x2+t23. В этом случае всем исходным событиям надо присвоить нули. Примером такой задачи является выбор оптимального из вариантов транспортировки, осуществляемых разными маршрутами из разных пунктов.
При нескольких завершающих событиях задача решается в отношении каждого из них поочередно.
Рассмотрим задачу на максимум пути.
В предлагаемой оптимизационной модели целевой функцией будет завершающее событие, минимум которого определяется, F= хn→ min; ограничения модели составляют неравенства для каждого события, которые имеют вид: xj≥xi+tij. Результатом будут ранние сроки свершения событий.
Меняя событие в целевой функции, можно решать частные задачи сетевого плана с позиций любого события системы, что бывает важно для понимания места и значимости конкретных событий и работ. Выбор системы ограничений определяет конкретную задачу — блок работ и событий.
В модель также могут быть включены дополнительные ограничения, лимитирующие параметры событий или работ.
В моделях с несколькими завершающими событиями целесообразно использовать в качестве целевой функции мах первого события — F1=max. Тогда будут получены все критические пути до каждого завершающего события. При этом в модели определяются поздние сроки свершения событий.
В таблице 1 показаны варианты решения сетевых планов.
Таблица 1.
Варианты решения сетевых планов.
|
Модель |
Варианты решения |
Переменные модели — х |
Целевая функция |
Ограничения |
|
критического пути |
Ранние сроки событий |
Ранние сроки свершения событий |
хn=min |
xj≥xi+tij
|
|
Поздние сроки событий |
Поздние сроки свершения событий |
х1= max |
xj≥xi+tij xn =A |
|
|
минимального пути
|
Ранние сроки событий |
Ранние сроки свершения событий |
хn=max |
xj≤xi+tij
|
|
Поздние сроки событий альтернатив-ные пути |
Поздние сроки свершения событий |
х1=min |
xj≤xi+tij xn =A |
Список литературы:
1. Заколодина Т. В., Люкманов В. Б., Мандыч И. А. Использование оптимизационного метода расчета сетевых планов для улучшения экологической обстановки на предприятии. Материалы /ГОУВПО Ивановский ГХТУ. Иваново, 2010, с. 477.
2. Люкманов В. Б., Мандыч И. А. Дополнительные возможности оптимизационного метода расчета сетевых планов // Вестник МИТХТ, ИПЦ МИТХТ им. М. В. Ломоносова, том VI, номер 4, Москва 2011 с. 116—117
3. Люкманов В. Б., Мандыч И. А., Цой А. В. // Двойственные оценки при решении сетевых задач оптимизационным методом. Журнал «Закон и право», № 1 (январь). М.: издательство Юнити-Дана. 2012 г., с. 118—119
дипломов


Оставить комментарий