ОСОБЕННОСТИ ТЕКСТУРИРОВАНИЯ ЗЕМНОЙ ПОВЕРХНОСТИ В ЗАДАЧЕ ПОВЫШЕНИЯ РЕАЛИСТИЧНОСТИ СИНТЕЗИРОВАННЫХ ЛАНДШАФТОВ

Мортин Константин Владимирович

Преподаватель, ГБОУ СПО ВО МТРП, г. Муром

E-mail: mortinkv@ya.ru

Карасев Олег Евгеньевич

канд. техн наук, доцент МИ (филиал) ВлГУ, г. Муром

LANDSCAPE TEXTURING FEATURES FOR SYNTHESIZED SURFACE IMPROVING

Konstantin Mortin

teacher of GBOU SPO IN MTRP, Murom

Oleg Karasev

Candidate. Technical., Associate Professor of MI (branch) of VLGU, Murom

АННОТАЦИЯ

В данной статье представлен новый метод текстурирования триангулированной синтезированной земной поверхности на основе наложения текстур на динамическую иррегулярную сетку, позволяющий повысить реалистичность по сравнению с известными алгоритмами наложения текстур.

ABSTRACT

In this work new texturing method for triangulated synthesized landscape is presented. It uses texturing algorithm for dynamic irregular net and provides better results than known texturing methods.

Ключевые слова: текстура; триангулированная синтезированная земная поверхность; иррегулярная сетка

Keywords: texture, triangulated synthesized landscape; irregular net.

Текстура представляет собой изображение с собственной системой координат. Пиксели текстуры (тексели) являются узловыми точками с координатами  (рис. 1).

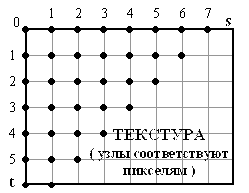
Рис. 1. Битовая карта текстуры

Определим трёхмерную сцену в системе координат  (рис. 2). Ось  пересекает центр экрана в точке .

Рис. 2. Пример треугольника в системе координат наблюдателя

Для текстурирования поверхности необходимо задать соответствие координат  текстуры координатам  поверхности.

Введём ортогональную систему координат  с осями, параллельными сторонам экрана. Пикселями экрана будем считать квадраты между соседними четвёрками с целочисленными координатами  и  (рис. 3).

Координаты текселей на карте текстуры являются целочисленными величинами, а координаты  – вещественными, и текселю не соответствуют. Поэтому необходимо преобразовать вещественные координаты  в значение цвета экранного пикселя.

Рис. 3. Пиксель в координатах  и его образ в координатах

При наложении текстуры методом множественного отображения (MIP Mapping) необходимо определить подходящий уровень детализации (LOD, Level of Details) [1]. Уровень LOD должен быть таким, чтобы размер образа экранного пикселя на текстуре и размер текселя текстуры были максимально близки. Размер текселя заданного уровня LOD можно вычислить следующим образом.

Рассмотрим пиксель как квадрат. Его образ в координатах  – есть произвольный четырехугольник. Изменение координаты  вдоль образа горизонтальной стороны пикселя вычисляется по формуле

Аналогично изменение координаты  вдоль образа горизонтальной стороны пикселя вычисляется через .

Заменяя в формулах  на , можно легко получить соотношения и для вертикальной стороны пикселя. Производные обычно приближаются конечными разностями значений на сторонах пикселей или соседей.

Используя аппроксимацию, можно применить следующие операции над пикселями:

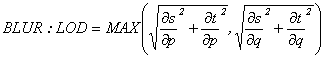 – даёт размытое изображение;

 – даёт резкое изображение;

 – является объединением предыдущих двух методов.

Объединяя эти три операции, можно добиться хорошего качества изображения. Вычисление производных и координат  в каждом пикселе производится также, как и в алгоритме быстрого отображения.

Переходим к проблеме вычисления значения цвета.

Для каждого пикселя экранной проекции можно вычислить трёхмерные координаты прообраза пикселя на поверхности треугольника, а по ним рассчитать координаты на текстуре. Обращение перспективного преобразования требует умножения на матрицу размера 4х4 для каждого пикселя проекции [2].

Для последовательности точек из отрезка значение линейной функции в любой из них вычислялось индуктивно, на базе значения функции в предыдущей точке.

Пусть мы движемся вдоль заданного на экране отрезка [p₁, p₂]. Прообраз отрезка [p₁, p₂] – отрезок [P₁, P₂] в пространстве, координаты концов которого (x₁, z₁), (x₂, z₂) нам известны (рис. 4).

Восстановим по точке  её прообраз P с координатами .

Рис 4. Система координат OXZ, отрезок [P1, P2], проекция на экран – отрезок [p1, p2], точка P и её проекция p

Запишем уравнение прямой, содержащей отрезок [P1, P2]: Ax+Bz+C=0.

При проективном преобразовании экранная координата p вычисляется как , откуда .

Подставляя выражение для x в уравнение отрезка [P1, P2], получим  или .

Выразим из этого соотношения , .

Введём вспомогательную величину .

 Для нее , а , что позволяет выразить  следующим образом: .

Воспользовавшись последним соотношением, найдем координаты точки

: .                                  (1)

Если не исключать из модели оси OY и q, то в системе (1) добавилось бы уравнение

 .                                      (2)

Пользуясь соотношениями (1) и (2), можно реализовать эффект перспективы в алгоритме быстрого наложения текстуры. Сохраняя величину  вместо z, мы сокращаем число отрезков, образующих треугольник.

В большинстве случаях размер накладываемой текстуры и размер текстурируемого треугольника (полигона) не совпадают. Поэтому, когда исходная текстура меньше, чем полигон, на который она накладывается, то текстура должна быть увеличена (растянута) до размеров полигона. И наоборот, когда текстура больше чем полигон, то она должна быть уменьшена (сжата) до размеров полигона.

Текстура поверхности – это детализация её строения, учитывающая микрорельеф и особенности окраски.

Во-первых, гладкая поверхность может быть покрыта каким-либо узором, и тогда при её изображении решается задача отображения этого узора на проекции фрагментов поверхности.

Во-вторых, поверхность может быть шероховатой, поэтому нужны специальные приёмы имитации такого микрорельефа при закрашивании.

Применяя в модели освещения новую нормаль, можно получить эффект шероховатости поверхности. В качестве функции возмущения можно использовать произвольную дифференцируемую по переменной функцию.

Список литературы:

1.Hoppe H. Smooth View-Dependent Level-of-Detail Control and its Application to Terrain Rendering // IEEE Visualization 1998 Conference. – P. 35–42.

2.Suen P, Healey G. The Analysis and Reconstruction of Real-World Textures in Three Dimensions // IEEE Transactions of Pattern Analysis and Machine Intelligence. – 2000. – Vol. 22. – No. 5. – P. 491–503.