Статья опубликована в рамках: XLV Международной научно-практической конференции «Инновации в науке» (Россия, г. Новосибирск, 27 мая 2015 г.)
Наука: Технические науки
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
МЕТОДИКА НАХОЖДЕНИЯ ОПТИМАЛЬНЫХ ПАРАМЕТРОВ РЕГУЛИРУЮЩИХ УСТРОЙСТВ
Кураев Сергей Валерьевич
аспирант Амурского государственного университета, РФ, г. Благовещенск
E -mail: SKuraew@yandex.ru
METHODS OF FINDING THE OPTIMAL PARAMETERS OF CONTROL DEVICES
Kuraev Sergey
graduate student at Amur state university, Russia, Blagoveshensk
АННОТАЦИЯ
В данной работе предложен метод поиска оптимальных параметров управляющих устройств, применяются методы аппроксимации и оптимизации, полученные результаты могут найти применение в широком спектре прикладных задач.
ABSTRACT
In this paper we propose a method for finding the optimal parameters of the control devices, used methods of approximation and optimization, the results can be used in a wide range of applications.
Ключевые слова: системы автоматического управления; поиск параметров; оптимизация.
Keywords : automatic control system; the search parameters; optimization.
Введение.
В задачах автоматического управления часто возникает необходимость выбрать параметры управляющих или корректирующих устройств. Обычно в таких случаях применяют либо приближенный метод нахождения параметров, так например для ПИД регуляторов применяются методы Чина-Ресвика-Хронса [4] и Зеглера-Николса [5], либо определяется диапазон допустимых значений и на нем производится ручная подстройка параметров. Однако вычислительные методы не являются универсальными и подходят лишь для узкого класса задач, а методы ручной подстройки могут занять много времени и не обеспечить максимального качества работы системы.
В данной работе предлагается метод поиска оптимальных параметров регуляторов и корректоров основанный на аппроксимации зависимости показателей качества от параметров регуляторов.
Постановка задачи.
Рассмотрим объект аналогичный [2]. Объект управления описывается уравнением:
![]()
![]() (1)
(1)
![]()
Функционирование протекает в условиях априорной неопределенности
![]() ,
,
здесь ξ — набор случайных параметров, удовлетворяющих гипотезе квазистационарности и принадлежащих известному множеству Ξ.
Для обеспечения устойчивости объекта к нему подключены два корректора. Параллельный корректор имеет вид:
![]() (2)
(2)
Последовательный корректор описывается уравнением:
![]() (3)
(3)
где: θ — малый положительный коэффициент,
a (p) — гурвицев полином,
b (p) — полином с произвольным расположением корней,
T 1, T2 — положительные коэффициенты,
p — оператор дифференцирования,
u (t) — управление.
Сформируем выход системы в виде:
![]() (4)
(4)
Управление объектом будем формировать следующим образом:
![]() (5)
(5)
![]() (6)
(6)
Применим следующий алгоритм настройки параметров
 (7)
(7)
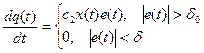 (8)
(8)
Где c1,c2=const>0, δ0>0 — достаточно малая величина, определяющая зону нечувcтвительности адаптивного регулятора.
Для системы (1)—(5) требуется найти такие параметры параллельного корректора (2) чтобы среднее арифметическое ошибки e(t)=r(t)-x(t) было минимальным. Диапазон параметров: 1,4<T1<6; 0,2<T2<0,8.
Решение задачи.
В качестве объекта исследования был выбран гидроагрегат Зейской ГЭС [3], с передаточной функцией вида:
![]() (9)
(9)
Для начала необходимо исследовать реакцию системы (1)—(5) на различные параметры корректора. Для этого испытаем систему с различными параметрами T1, T2 и оценим среднюю ошибку управления ![]() .
.


Рисунок 1. Зависимость средней ошибки от параметров корректора
На рисунке 1 представлен объемный график зависимости средней ошибки управления от параметров корректора. Задачи, в которых требуется найти один или два параметра, можно решить графическим методом, хотя при большом диапазоне допустимых значений это может потребовать большого количества испытаний. Для числа параметров больше двух такой способ окажется неприемлемым.
Для решения поставленной задачи можно аппроксимировать поверхность, описывающую зависимость, приближенной функцией вида:
![]() ,(10)
,(10)
где αi, βi, γ — неизвестные коэффициенты, которые будут найдены в процессе аппроксимации. Подобную аппроксимацию можно применить и для большего числа параметров регуляторов или корректоров.


Рисунок 2. Аппроксимация зависимости средней ошибки
На рисунке 2 показана аппроксимирующая поверхность, построенная полиномами 3-го порядка с помощью метода наименьших квадратов [5]. Построение подобной аппроксимации не требует большого числа испытаний системы и позволяет значительно сократить время, затрачиваемое на исследование поведения системы.
Найти минимум такой функции не сложно, например, методом наискорейшего спуска [3].

Рисунок3. динамика поведения системы
На рисунке 3 приведено сравнение динамики объекта с наименьшей ошибкой управления и динамики объекта с большей средней ошибкой.
Заключение.
Предложенный метод позволяет находить оптимальные параметры регулирующих элементов, не зависимо от типа системы и ее сложности. В зависимости от поставленной задачи можно изменять сложность аппроксимирующей функции и количество испытаний системы. Недостатками метода являются — необходимость проведение ряда испытаний с различными параметрами регуляторов, что не всегда возможно, а так же вследствие использования аппроксимации более низкая точность по сравнению с аналитическими методами.
Список литературы:
- Дудченко Л.Н. Регулирование частоты и активной мощности в энерго-системе. Препринт. Благовещенск. Амурский гос. ун-т. 1997. — 74 с.
- Еремин. Е.Л. Адаптивное шунтирование в системах управления неминимально-фазовыми объектами. // Информатика и системы управления. Благовещенск. Амурский гос. ун-т. 2001. — с. 74—82.
- Калиткин Н.Н. Численные методы. М. Наука. 1978. — 512 с.
- Chien K.L., Hrones J.A., Reswick J.B. On automatic control of generalized passive systems. Trans. ASME, 1974, — p.p. 175—185.
- Ziegler J.G., Nichols N.B. Optimum settings for automatic controllers. Trans. ASME, — vol. 64, — 1942, — p. 759—768.
дипломов


Оставить комментарий