Статья опубликована в рамках: XLVII Международной научно-практической конференции «Инновации в науке» (Россия, г. Новосибирск, 29 июля 2015 г.)
Наука: Технические науки
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
ОБЗОР РАБОТ ПО ГАЗОДИНАМИЧЕСКИМ РАЗРЫВАМ
Булат Павел Викторович
канд. физ.-мат. наук, руководитель лаборатории «НМиНКБС_СВЧ_ЭиМ», Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования Санкт-Петербургский национальный исследовательский университет информационных технологий, механики и оптики,
РФ, г. Санкт-Петербург
Е- mail: pavelbulat@mail.ru
Продан Николай Васильевич
инженер лаборатории «НМиНКБС_СВЧ_ЭиМ»,
Федеральное государственное бюджетное образовательное учреждение высшего профессионального образования Санкт-Петербургский национальный исследовательский университет информационных технологий, механики и оптики,
РФ, г. Санкт-Петербург
Е- mail: kolinti@mail.ru
GAS-DYNAMIC WAVES AND DISCONTINUITIES
Pavel Bulat
с andidate of Science, Head of laboratory «NMiNKBS_SVCh_JeiM»,
Saint-Petersburg National Research University of Information Technologies, Mechanics and Optics,
Russia, Saint-Petersburg
Nikolay Prodan
engineer of laboratory «NMiNKBS_SVCh_JeiM», Saint-Petersburg National Research University of Information Technologies, Mechanics and Optics,
Russia , Saint-Petersburg,
АННОТАЦИЯ
В статье приведен обзор работ в области изучения газодинамических разрывов, возникающих в сверхзвуковых течениях газа. Вводится понятие ударной волны, скачка уплотнения и ударной поляры. На примере этапных научных работ показано становление представлений об ударных волнах как узкой области с резким изменением газодинамических параметров. Описана связь между физической природой газодинамических разрывов и появлением особенностей в решениях уравнений Эйлера для идеального газа. Исследования выполнены при финансовой поддержке Министерства образования и науки РФ (Соглашение № 14.575.21.0057).
ABSTRACT
In this paper we examine the history of the studying the dynamic compatibility conditions for gas-dynamic discontinuities, which determine the ratio between values of the gas-dynamic variables before the discontinuity and right behind him. The concepts of a shock wave, shock and the shock polar are introduced. The formation of ideas about the shock waves as a narrow region with abrupt changes in gas-dynamic parameters is shown with a staged scientific studies as an example. The relationship between the physical nature of gas-dynamic discontinuities and the appearance of singularities in solutions of the Euler equations for an ideal gas is shown. The researches are executed with the financial support of the Ministry of Education and Science of the Russian Federation (the Agreement № 14.575.21.0057).
Ключевые слова : ударная волна; газодинамический разрыв; условия динамической совместности; ударная поляра.
Keywords : shock waves; gas-dynamic discontinuity; conditions of dynamic compatibility; shock polar.
ВВЕДЕНИЕ
Цель — показать на примере наиболее значимых научных работ, как происходило становление основных понятий теории ударных волн. Рассматривается история изучения условий динамической совместности на газодинамических разрывах, определяющих соотношение значений газодинамических переменных до разрыва и сразу за ним. Вводится понятие ударной волны, скачка уплотнения и ударной поляры.
Рассмотрена связь между понятием газодинамических разрывов и природой гиперболических уравнений в частных производных.
1. Математическая модель и природа газодинамических разрывов
Моделью ударных волн![]() является поверхность математического разрыва первого рода, при переходе через которую газодинамические переменные терпят разрыв
является поверхность математического разрыва первого рода, при переходе через которую газодинамические переменные терпят разрыв ![]() . Принято разделять волны разряжения
. Принято разделять волны разряжения ![]() (нестационарная простая изоэнтропическая волна Римана) и
(нестационарная простая изоэнтропическая волна Римана) и ![]() (стационарная центрированная волна Прандтля-Майера) в которых отношение статических давлений
(стационарная центрированная волна Прандтля-Майера) в которых отношение статических давлений![]() и волны уплотнения (сжатия)
и волны уплотнения (сжатия) ![]() ,
,![]() и
и ![]() (ударная волна), в которых
(ударная волна), в которых ![]() . Соотношения переменных
. Соотношения переменных ![]() и
и ![]() по разные стороны газодинамических разрывов получили название условий динамической совместимости (УДС) [8]. УДС на стационарных разрывах представляют собой балансы удельных потоков [6]
по разные стороны газодинамических разрывов получили название условий динамической совместимости (УДС) [8]. УДС на стационарных разрывах представляют собой балансы удельных потоков [6]
· вещества
![]() , (1)
, (1)
· нормальной
![]() (2)
(2)
· и тангенциальной компонент импульса
![]() , (3)
, (3)
· энергии
![]() , (4)
, (4)
где ![]() и
и ![]() проекции вектора скорости на плоскость разрыва. В таком виде УДС появились не сразу. Дифференциальные уравнения относительно плотности
проекции вектора скорости на плоскость разрыва. В таком виде УДС появились не сразу. Дифференциальные уравнения относительно плотности ![]() и потенциала скорости
и потенциала скорости ![]() , описывающие одномерные нестационарные движения невязкого совершенного изотермического газа, впервые представлены в 1788 году в книге Лагранжа [17], формулы даны, как в оригинале:
, описывающие одномерные нестационарные движения невязкого совершенного изотермического газа, впервые представлены в 1788 году в книге Лагранжа [17], формулы даны, как в оригинале:
![]() ; (5)
; (5)
![]() . (6)
. (6)
Здесь a — скорость звука, D — плотность первоначально невозмущенной среды. Для связи между давлением, плотностью и скоростью звука Лагранж использовал соотношение, ранее предложенное Ньютоном:
![]() . (7)
. (7)
Производная ![]() представляет собой скорость газа, в 1808 году Пуассон [18] получил для нее выражение в виде плоской волны:
представляет собой скорость газа, в 1808 году Пуассон [18] получил для нее выражение в виде плоской волны:
![]() , (8)
, (8)
где F — некоторая произвольная функция, определяемая начальными и/или граничными условиями.
В 1848 году Стокс [24] обратил внимание на то, что решения этих уравнений остаются непрерывными только в течение ограниченного промежутка времени. Интересно, что именно в такой постановке задача изучения движения идеального газа, содержащего разрывы, рассматривалась в конце XX-ого века научной школой советского математика В.И. Арнольда [1].
Уравнение (8) описывает поле скоростей свободно движущихся по прямой частиц. Закон свободного движения частицы имеет вид x=ϕ(t)=x0+ut, где u –скорость частицы. Функция ϕ удовлетворяет уравнению Ньютона. По определению dϕ/dt =u(t, ϕ). Продифференцировав последнее соотношение по t, приходим к уравнению, получившему название уравнения Эйлера
![]() . (9)
. (9)
Таким образом, описание движения при помощи уравнения Эйлера для поля газодинамических переменных и при помощи уравнения Ньютона для частиц эквивалентны. Известно, что квазилинейные дифференциальные уравнения в частных производных решаются с помощью построения характеристик. Характеристики уравнения Эйлера эквивалентны закону Ньютона для движущейся частицы [2] и задачу о распространении волны можно решить путем построения характеристик, вдоль которых движутся материальные частицы. На рисунке 1 показано, как решается уравнение Эйлера с помощью характеристик.
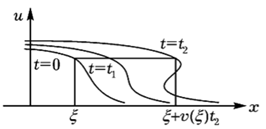

Рисунок 1. Решение уравнения Эйлера с помощью характеристик
На плоскости y-x задана начальная функция y=u0(x)t=0. Уравнения характеристик - t’=1, y’=0, x’=y. Если отложить от этой кривой горизонтальные линии, то вдоль каждой из них частицы будут двигаться со своей постоянной скоростью. Тогда в некоторые моменты времени t=t1, t2 … tn форма распределения скорости u(x) будет меняться (рисунок 2).

Рисунок 2. Появление неоднозначности в решении
В некоторый момент времени (t2 на рисунке 2) отображение u(x) перестает быть графиком функции, т. е. имеются значения х, которым соответствует несколько значений u. В этой области физическое условие отсутствия взаимодействия частиц означает их прохождение сквозь друг друга, что нефизично. Нужно вводить некоторую модель их взаимодействия. Например, в модели образования вселенной, предложенной Я.Б. Зельдовичем [29], учитывается расширение вселенной и гравитационное взаимодействие. Добавление таких условий приводит к появлению особенностей в решении, т. е. областей, где концентрация частиц (у Зельдовича галактик) максимальна. Такие области (множество критических значений) называются каустиками (рисунок 3).

Рисунок 3. Каустика волны
Однажды возникнув, каустика может трансформироваться, распадаться с образованием новых особенностей, но не может исчезнуть. Данная модель хорошо описывает образование неравномерной (ячеистой) структуры вселенной из первоначальных случайных флуктуаций плотности вещества и энергии.
В рассматриваемом нами примере сверхзвукового течения идеального газа необходимо ввести модель неупругого столкновения частиц. Тогда в месте этого столкновения будет образовываться ударная волна — разрыв параметров движения частиц (рисунок 1 справа). В решении появляются разрывы, т. к. уравнение поля Эйлера перестает однозначно описывать распределение газодинамических переменных. Стокс в упомянутом выше труде первым ввел понятие разрыва (discontinuity) в области течения сплошной среды и получил два условия для плотности ρ и скорости газа u по сторонам разрыва, следующие из законов сохранения массы и количества движения:
![]() ; (10)
; (10)
![]() . (11)
. (11)
Здесь ![]() — скорость распространения разрыва, индексом "2" обозначены параметры за ним, индексом "1" — параметры до него (рисунок 4).
— скорость распространения разрыва, индексом "2" обозначены параметры за ним, индексом "1" — параметры до него (рисунок 4).

Рисунок 4. Газодинамический разрыв
Такие разрывы, на которых газодинамические параметры меняются скачком, впоследствии назвали сильными. Стокс отметил, что скачкообразное изменение параметров на разрывах является результатом пренебрежения вязкостью и теплопроводностью среды.
Простейшей моделью неупругого столкновения частиц является уравнение Бюргерса [4], которое описывает газодинамическое поле в гладких областях пространства, и взаимодействие частиц газа внутри ударной волны
![]() . (12)
. (12)
При малой вязкости ε оно приближает уравнение Эйлера в областях плавного изменения параметров (рисунок 5). Справа и слева от ударной волны течение описывается уравнениями Эйлера, внутри ударной волны (газодинамического разрыва) — уравнением подобным уравнению теплопроводности.


Рисунок 5. Замена уравнения Эйлера (слева) уравнением Бюргерса (справа)
Ирншоу [14], [15] рассмотрел одномерные нестационарные течения газа, как изотермические, так и адиабатические. Им были получены решения в виде плоской волны, в которой с течением времени образуются области резкого изменения параметров, которые он, как и Стокс, назвал разрывами. Важную роль в анализе газодинамических разрывов, сверхзвуковых движений газа играет скорость распространения возмущений — скорость звука. Ирншоу ввел следующую связь между давлением, плотностью и адиабатической скоростью звука:
![]() ,
, ![]() , (13)
, (13)
где k — отношение удельной теплоемкости газа при постоянном давлении к удельной теплоемкости при постоянном объеме. Сейчас стандартным считается обозначение ![]() .
.
2. Условия динамической совместности на разрыве
Сформулированных Стоксом условий (10—11) недостаточно, чтобы определить два неизвестных параметра потока за разрывом и скорость распространения самого разрыва. Первой попыткой замкнуть написанную Стоксом систему уравнений была опубликованная в 1860 году работа Римана [22]. В этой работе автор предположил, что при переходе через нормальный разрыв энтропия постоянна, и дополнил систему (10—11) третьим уравнением. Объяснить возникающее при этом предположении изменение энергии при переходе через разрыв Риман не смог.
Независимо от Римана, Рэнкин в 1869—1870 годах [19], [20], [21] получил третье уравнение, дополняющее систему (10—11), в другом виде. Он установил связь между параметрами по сторонам ударной волны, рассмотрев непрерывно меняющиеся внутри нее состояния среды, в которой происходит равновесный теплообмен. Суммарное количество теплоты, полученное средой, должно быть равно нулю. Используя соотношения равновесной термодинамики и формулы Стокса, Рэнкин получил выражения для скорости распространения нормального разрыва по неподвижной среде a (не путать со скоростью звука а) и скорости потока за ним u через известные давления до разрыва P и за ним p, а также известный удельный объем до разрыва S для совершенного газа (обозначения, как в оригинале):
![]() . (14)
. (14)
Наиболее важным результатом Рэнкина является утверждение, что нормальные разрывы всегда распространяются относительно неподвижной среды со сверхзвуковой скоростью, в то время как относительно среды за разрывом их скорость распространения всегда дозвуковая. Способ получения УДС на ударной волне, примененный Рэнкиным, приводит к выполнению всех законов сохранения, но он учитывает теплопроводность газа, а его вязкостью пренебрегает, что не слишком обосновано, т. к. вязкость и теплопроводность взаимосвязаны. Гюгонио получил условие на нормальном разрыве более строго, чем Рэнкин, как следствие закона сохранения энергии, минуя рассмотрение состояния газа «внутри» ударной волны [16]. Это условие совпадает с полученным ранее условием Рэнкина, но для его вывода Гюгонио не потребовалось дополнительных предположений.
Сегодня УДС на стационарных разрывах представляют балансы удельных потоков [6]
· вещества
![]() , (15)
, (15)
· нормального
![]() (16)
(16)
· и тангенциальной компонент импульса
![]() , (17)
, (17)
· компонент энергии
![]() , (18)
, (18)
Где ![]() и
и ![]() проекции вектора скорости на плоскость разрыва. Из (15—18) следует, что существует 2 вида разрывов: тангенцальный (
проекции вектора скорости на плоскость разрыва. Из (15—18) следует, что существует 2 вида разрывов: тангенцальный (![]() , где
, где ![]() ) и нормальный (скачок уплотнения) через который газ перетекает. Из (16) видно, что по обе стороны
) и нормальный (скачок уплотнения) через который газ перетекает. Из (16) видно, что по обе стороны ![]() статические давления одинаковы, а из (17), что тангенциальные составляющие могут быть различными, т. е.
статические давления одинаковы, а из (17), что тангенциальные составляющие могут быть различными, т. е. ![]() являются линиями скольжения. Разными могут быть плотности, температуры, полные теплосодержания и энтропии потоков, разделенных тангенциальными разрывами.
являются линиями скольжения. Разными могут быть плотности, температуры, полные теплосодержания и энтропии потоков, разделенных тангенциальными разрывами.
Из приведенной системы несложно получить адиабаты Лапласса-Пуассона (изоэнтропу)
![]() (19)
(19)
и Рэнкина-Гюгонио (ударную адиабату)
![]() (20)
(20)
где ![]() ,
, ![]() показатель адиабаты,
показатель адиабаты, ![]() ,
, ![]() интенсивность ударно-волнового процесса уплотнения (J>1) или разрежения (J<1). Изоэнтропа (19) справедлива для простых волн сжатия (J>1) и разрежения (J<1) стационарных (волн Прандтля-Майера) или бегущих (волн Римана). Ударная адиабата (20) появилась именно в результате моделирования скачков уплотнения и ударных волн поверхностями разрыва. Числа Маха по разные стороны волны или разрыва связаны формулой
интенсивность ударно-волнового процесса уплотнения (J>1) или разрежения (J<1). Изоэнтропа (19) справедлива для простых волн сжатия (J>1) и разрежения (J<1) стационарных (волн Прандтля-Майера) или бегущих (волн Римана). Ударная адиабата (20) появилась именно в результате моделирования скачков уплотнения и ударных волн поверхностями разрыва. Числа Маха по разные стороны волны или разрыва связаны формулой
![]() (21)
(21)
где ![]() и
и ![]() . В зависимости от того, какую формулу для адиабаты подставляем, ударной адиабаты (16) или изоэнтропы (15), формула (17) дает возможность определить числа Маха за волнами разрежения/сжатия
. В зависимости от того, какую формулу для адиабаты подставляем, ударной адиабаты (16) или изоэнтропы (15), формула (17) дает возможность определить числа Маха за волнами разрежения/сжатия ![]() и скачками
и скачками ![]() уплотнения.
уплотнения.
В прямых ударных волнах соотношения ![]() и
и ![]() устанавливаются из системы (11—14), в которой скорость D — скорость перемещения ударной волны по исходному потоку, имеющему скорость U [5]
устанавливаются из системы (11—14), в которой скорость D — скорость перемещения ударной волны по исходному потоку, имеющему скорость U [5]
![]() , (22)
, (22)
которое приводит указанную систему УДС к виду УДС — D:
![]() ; (23)
; (23)
![]() ;
; ![]() ; (24)
; (24)
![]() . (25)
. (25)
При D=0 система (22—25) описывает УДС на прямом скачке уплотнения.
Из (22) видно, что при D=U (![]() ) величина
) величина ![]() , т. е.
, т. е. ![]() , и существует поверхность разрыва переменных, через которую газ не перетекает. Такой разрыв является контактным (
, и существует поверхность разрыва переменных, через которую газ не перетекает. Такой разрыв является контактным (![]() ). Он перемещается со скоростью газов
). Он перемещается со скоростью газов ![]() и разделяет потоки с разными термодинамическими переменными (кроме статических давлений
и разделяет потоки с разными термодинамическими переменными (кроме статических давлений ![]() , как и на тангенциальных разрывах). В силу уравнений Клайперона
, как и на тангенциальных разрывах). В силу уравнений Клайперона
![]() (26)
(26)
для совершенного газа (![]() ) на
) на ![]() выполняются равенства
выполняются равенства
![]() ,
, ![]() . (27)
. (27)
Таким образом, контактный разрыв представляет собой особую поверхность, разделяющую газы с различными термодинамическими параметрами (кроме давлений) [25].
Из УДС-D (25) также видно, что в отличие от скачков уплотнения на ударных волнах имеет место и разрыв полного теплосодержания. Сами прямые скачки являются частными случаями стоячих ударных волн (D=0) в сверхзвуковых потоках газа.
3. Ударная поляра, сердцевидные кривые
Подробный анализ газодинамических волн (изоэнтропических волн разрежения и сжатия) и косых скачков уплотнения, возникающих в плоских стационарных течениях невязкого нетеплопроводного совершенного газа, был опубликован в 1908 году Т. Майером. В этой же работе определены параметры косого скачка уплотнения, образующегося при обтекании плоского острого угла. Это задача является важной для практики, т. к. обтекание наклонной преграды — одна из часто встречающихся причин появления скачка уплотнения в потоке газа. Начиная с этой работы Мейера, в качестве основного параметра, характеризующего скачок уплотнения, рассматривают его интенсивность - отношение статических давлений ![]() по его сторонам. В современном виде УДС на скачках уплотнения были сформулированы В.Н. Усковым в 1980 г. В дальнейшем они были развиты на случай одномерных бегущих волн, а также косых ударных волн [11]. В этих работах приведены удобные формулы для расчета параметров косых скачков уплотнения и косых ударных волн. В частности, для интенсивности косых скачков (
по его сторонам. В современном виде УДС на скачках уплотнения были сформулированы В.Н. Усковым в 1980 г. В дальнейшем они были развиты на случай одномерных бегущих волн, а также косых ударных волн [11]. В этих работах приведены удобные формулы для расчета параметров косых скачков уплотнения и косых ударных волн. В частности, для интенсивности косых скачков (![]() ) уплотнения
) уплотнения
![]() . (28)
. (28)
Здесь σ — угол наклона вектора скорости к плоскости скачка, который может изменяться в пределах ![]() , где
, где ![]() — угол Маха, при ктором скачок вырождается в линию Маха (
— угол Маха, при ктором скачок вырождается в линию Маха (![]() ). Значения J определяют и другие газодинамические переменные за разрывами: плотности с помощью ударной адиабаты, температуры (
). Значения J определяют и другие газодинамические переменные за разрывами: плотности с помощью ударной адиабаты, температуры (![]() ), скорости звука (
), скорости звука (![]() ). Угол поворота потока на скачках также определяется интенсивностями
). Угол поворота потока на скачках также определяется интенсивностями ![]() и
и ![]()
![]() . (29)
. (29)
Здесь ![]() . В координатах
. В координатах![]() формулы (28,29) описывает семейство кривых (рисунок 6), прозванных за их характерный внешний вид сердцевидными. Другое их название — ударные поляры. Проведенное В.Н. Усковым [9] исследование сердцевидных кривых позволило установить их важные свойства: наличие огибающей, предельных углов отклонения потока на разрыве, точек, соответствующих разрывам, числа Маха за которыми равны единице. Можно отметить, что наличие огибающей важно в задачах сверхзвуковой аэродинамики [12], т. к. соответствует экстремумам давления на сторонах тела, летящего с заданным углом атаки, но с переменной скоростью.
формулы (28,29) описывает семейство кривых (рисунок 6), прозванных за их характерный внешний вид сердцевидными. Другое их название — ударные поляры. Проведенное В.Н. Усковым [9] исследование сердцевидных кривых позволило установить их важные свойства: наличие огибающей, предельных углов отклонения потока на разрыве, точек, соответствующих разрывам, числа Маха за которыми равны единице. Можно отметить, что наличие огибающей важно в задачах сверхзвуковой аэродинамики [12], т. к. соответствует экстремумам давления на сторонах тела, летящего с заданным углом атаки, но с переменной скоростью.

Рисунок 6. Ударные поляры
Получены результаты для оптимальных (в смысле достижения экстремума некоторого параметра) одномерных бегущих [7] и двухмерных косых ударных волн [10]. Соотношения, описывающие сердцевидные кривые, известны давно, но их использование до сих пор нередко вызывает затруднения из-за имеющихся вычислительных особенностей и необходимости отбора из множества формальных корней. Первые количественные экспериментальные результаты, которые можно было бы сравнить с теорией, получены Вьелем в 1899 году [27]. Он проводил измерения скорости распространения ударной волны в трубе после разрыва мембраны (прообраз современной ударной трубы). Стодола в 1903 году [23] изучал течения внутри сопла на режиме с пусковым скачком уплотнения внутри него. Эти исследования позволили получить экспериментальное подтверждение теории Стокса, Римана, Рэнкина и Гюгонио для одиночного разрыва. Обобщение результатов исследования газодинамических разрывов и условий динамической совместности на них приведено в работах [3], [13], [26], [28].
ЗАКЛЮЧЕНИЕ
В приведенном обзоре даны ссылки на наиболее важные и этапные научные работы, посвященные нахождению соотношений на скачках уплотнения, ударных волнах, простых (изоэнтропических) волнах сжатия и разрежения. Введено понятие газодинамического разрыва как поверхности, на которой терпят разрыв газодинамические переменные. Показана связь с геометрической теорией уравнений в частных производных. Введено понятие ударной поляры, приведены основные работы, в которых изучались свойства ударных поляр.
Список литературы:
- Арнольд В.И. Геометрические методы в теории обыкновенных дифференциальных уравнений. Ижевск: Ижевская республиканская типография. 2000. — 400 с.
- Арнольд В.И. Дополнительные главы теории обыкновенных дифференциальных уравнений. Учебное пособие для студентов физико-математических специальностей высших учебных заведений. М: Издательство 'Наука'. Главная редакция физико-математической литературы, 1978. — 367 с.
- Булат П.В. Ударная и детонационная волна с точки зрения теории интерференции газодинамических разрывов — геометрический смысл уравнений газовой динамики сверхзвуковых течений / П.В. Булат // Журн.Фундаментальные исследования — 2013. — № 10, — Ч. 9. — С. 1951—1954.
- Теоретическая аэродинамика идеальных жидкостей./ Т. Карман и И. Бюргерс, 1939. — 408 стр. с.: с илл. и черт.; 23 см. — в пер., тираж: 3000 экз.
- Усков В.Н. Бегущие одномерные волны. СПб: БГТУ ВОЕНМЕХ. 2000. — 224 с.
- Усков В.Н. Интерференция стационарных газодинамических разрывов/ “Сверхзвуковые Газовые Струи”. Новосибирск: ИТПМ, 1983. — С. 22—46.
- Усков В.Н. Оптимальные Бегущие По Потоку Газа Одномерные Волны. Доклады на XV сессии Международной школы по моделям механики сплошной среды. 2000. — С. 63—78.
- Усков В.Н. Ударные волны и их взаимодействие. Л.: ЛМИ, 1980. — 88 с.
- Усков В.Н., Адрианов А.Л., Старых А.Л. Интерференция стационарных газодинамических разрывов. Новосибириск: ВО “Наука”. Сибирская Издательская Фирма. 1995. — С. 180.
- Усков В.Н., Мостовых П.С. Экстремальные Свойства Косой Ударной Волны, Бегущей По Потоку Газа.// Четвертые Поляховские чтения: Избранные труды. СПб: ВВМ. 2006. — С. 444—454.
- Усков В.Н., Тао Ган, Омельченко А.В. О Поведении Газодинамических Переменных За Косой Ударной Волной/ Сб. статей// Под. ред. В.Н. Ускова. 2002. — С. 179—191.
- Усков В.Н., Чернышов М.В. Экстремальные ударно-волновые системы в задачах внешней аэродинамики // Теплофизика и аэромеханика. — Т. 21. — 2014. — № 1. — C. 15—31.
- Bulat P.V., Uskov V.N., 2014. Shock and detonation wave in terms of view of the theory of interaction gasdynamic discontinuities. Life Science Journal, 11(8s): 307-310.
- Earnshaw S. On the mathematical theory of sound // Philosophical Transactions, — Vol. 150. — 1860. — № 8. — p. 133—148.
- Earnshaw S. On the Mathematical Theory of Sound // Proceedings of the Royal Society of London, III. — 1858. — p. 590—591. [Электронный ресурс] — Режим доступа. — URL: http://www.lifesciencesite.com/lsj/life1108s/068_24921life1108s14_307_310.pdf
- Hugoniot H. (1889) Propagation du mouvement dans les corps. Chapitre V. Sur les discontinuit ́es qui se manifestent dans la propagation du mouvement // Journal de l’E ́cole Polytechnique, cahier LVIII. 1889. — p. 68—125.
- Lagrange J.L. Mecanique analytique/ Œuvres de Lagrange//Tome douzieme. Paris, 1788.
- Poisson S.D. Memoire sur la theorie du son // Journal de l’Ecole Polytechnique, t. VII, cahier 14, 1808. — p. 319—392.
- Rankine. On the thermodynamic theory of waves of finite longitudinal disturbance // Proceedings of the Royal Society of London, Vol. XVIII. — 1869 — № 115, III, — p. 80—84.
- Rankine. On the thermodynamic theory of waves of finite longitudinal disturbance // Philosophical Magazine, Series 4, — Vol. 39. — 1870. — № CCLXI, — p. 306—309.
- Rankine. On the thermodynamic theory of waves of finite longitudinal disturbance // Philosophical Transactions, — Vol. 160, — Part II. — 1870. — XV, — p. 277—288.
- Riemann B. Uber die Fortpflanzung ebener Luftwellen von end- licher Schwingweite // Abhandlungen der koniglichen Gesellschaft der Wissenschaften zu Gottingen, Bd. 8. 1860. — S. 43.
- Stodola A. Beitrag zur Stromung von Gasen und D ̈ampfen durch Rohre mit veranderlichem Querschnitt // Zeitschrift des Vereins deutcher Ingenieure, — Bd. 47. — 1903. — № 49, 5. Dezember. — S. 1787—1788.
- Stokes G.G. On a difficulty in the theory of sound // Philosophical Magazine, Series 3, Vol. 33, November, LIV, 1848. — p. 349—356.
- Uskov V.N. Interference of Stationary and Non Stationary Shock Waves. Shock Waves., — Vol. 20. — 2010. — № 2. — P. 119—129.
- Uskov V.N., Bulat P.V., Arkhipova L.P. Gas-dynamic Discontinuity Conception. Research Journal of Applied Sciences, Engineering and Technology, — 2014, — Vol. 8, (22). — p. 2255—2259.
- Uskov V.N., Chernyshov M.V. Extreme shockwave systems in problems of external supersonic aerodynamics // Thermophysics and Aeromechanics. — Vol. 21. — 2014. — № 1. — p. 15—30.
- Vieille P. Sur les discontinuiti ́es produites par la det ́ente brusque de gaz comprim ́es // Comptes Rendus, — t. CXXIX. — 1899. — p. 1228—1230.
- Vladimir Nikolaevich Uskov, Pavel Viktorovich Bulat and Lyubov Pav-lovna Arkhipova, 2014. Classification of Gas-dynamic Discontinuities and their Interference Problems. Research Journal of Applied Sciences, Engineering and Technology, 8(22): 2248-2254.
- Zeldovich Ya., B. Gravitational instability: an approximation theory for large density perturbation. Astron. Astrophys. 1970, 5(1), 85-89.
дипломов


Оставить комментарий