ПОСТРОЕНИЕ  РЕШЕНИЯ  ИНТЕГРО-ДИФФЕРЕНЦИАЛЬНОГО  УРАВНЕНИЯ  РИККАТИ

Копец  Мирослав  Михайлович

канд.  ф.-мат.  наук,  доцент  кафедры  математической  физики  Национального  технического  университета  Украины  «Киевский  политехнический  институт»,  г.  Киев,  Украина

E-mail: 

CREATION  OF  SOLUTION  OF  THE  INTEGRO-DIFFERENTIAL  EQUATION  OF  RICCATI

Kopets  Miroslav

candidate  of  Physical  and  Mathematical  Sciences,  associate  professor  of  Mathematical  Physics  Chair,  National  Technical  University  of  Ukraine  ‘Kyiv  Polytechnic  Institute’,  Kyiv,  Ukraine

АННОТАЦИЯ

В  данной  статье  рассматривается  проблема  минимизации  квадратичного  функционала  на  решениях  первой  краевой  задачи  для  уравнения  теплопроводности.  Для  исследования  сформулированной  задачи  оптимизации  применен  метод  множителей  Лагранжа.  Такой  подход  дал  возможность  получить  необходимые  условия  оптимальности.  На  основе  этих  условий  выведено  интегро-дифференциальное  уравнение  Риккати  с  частными  производными.  Решение  этого  уравнения  представлено  в  замкнутой  форме. 

ABSTRACT

In  the  article  the  stated  problem  is  the  problem  of  minimization  of  quadratic  functional  while  finding  the  solution  of  the  Dirichlet  boundary  value  problem  for  the  thermal  conductivity  equation.  For  the  purpose  of  study  of  the  given  optimization  objective  there  is  the  Lagrange  multiplier  method  used.  Such  approach  allows  getting  the  necessary  criteria  of  optimality.  Based  on  those  conditions  there  is  elicited  the  integro-differential  equation  of  Riccati  with  partial  derivatives.  The  solution  for  this  equation  is  expressible  in  an  essentially  closed  form. 

Ключевые  слова:  дельта-функция  Дирака;  интегро-дифференциальное  Риккати;  метод  множителей  Лагранжа;  необходимые  условия  оптимальности;  оптимальное  управление;  процесс  теплопроводности.

Key  words:  delta  function  of  Dirac;  integro-differential  equation  of  Riccati;  Lagrange  multiplier  method;  necessary  criteria  of  optimality;  optimal  control;  process  of  thermal  conductivity. 

Введение

В  теории  оптимального  управления  линейно-квадратическая  задача  играет  весьма  существенную  роль.  Она  возникает  при  построении  оптимального  управления  по  принципу  обратной  связи  [6],  при  нахождении  оптимальных  фильтров  Калмана-Бьюси  [7]  ,  в  теории  дифференциальных  игр  [3].  С  каждой  такой  задачей  непосредственно  связано  матричное  дифференциальное  или  алгебраическое  уравнение  Риккати.  В  случае,  когда  исследуются  системы  с  сосредоточенными  параметрами,  это  уравнение  изучено  достаточно  полно.  Для  систем  с  распределенными  параметрами  ситуация  является  не  столь  однозначной.  Например,  в  монографии  [4]  рассматриваются  операторные  уравнения  Риккати,  исследуемые  методами  функционального  анализа.  В  монографиях  [1],  [2],  [8]  данный  вопрос  не  рассматривается.  Настоящая  статья  посвящена  исследованию  линейно-квадратической  задаче  оптимального  управления  процессом  теплопроводности.  С  использованием  методом  множителей  Лагранжа  для  рассматриваемой  задачи  оптимизации  получены  необходимые  условия  оптимальности.  С  их  помощью  построено  интегро-дифференциальное  уравнение  Риккати  с  частными  производными,  решение  которого  представлено  замкнутой  форме.

Постановка  задачи

Рассматривается  задача  минимизации  функціонала

  (1)

на  решениях  следующей  краевой  задачи

,  (2)

,  ,  ,  (3)

где  действительные  числа  ,  ,    и  функция    заданы.  Функция    называется  допустимым  управлением,  если  ,  где  множество    имеет  вид:  .  Для  фиксированного  допустимого  управления    решением    задачи  (2)—(3)  считается  обобщенное  решение  .  Допустимое  управление  ,  на  котором  реализуется  минимум  функционала  (1),  називается  оптимальным  управлением.

Необходимые  условия  оптимальности

Необходимые  условия  оптимальности  для  сформулированной  выше  задачи  оптимизации  можно  найти  с  помощью  метода  множителей  Лагранжа  [5,  с.  31].  Для  этого  рассмотрим  следующий  вспомогательный  функціонал

,  (4)

где  функция    —  множитель  Лагранжа.  Таким  способом  задача  (1)—(3)  на  условный  экстремум  сводится  к  задаче  минимизации  функционала  (4)  с  учетом  условий  (3).  Дальше,  используя  стандартный  способ  вариационного  исчисления,  найдем  приращение    функционала  (4)

.  (5)

В  развернутом  виде  соотношение  (5)  запишется  следующим  образом 

.

.  (6) 

После  очевидних  упрощений  (раскрытия  скобок,  интегрирования  по  частям  и  та  приведения  подобных  членов)  вместо  равенства  (6)  получим  следующее  соотношение

.

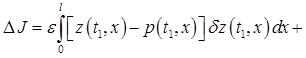
.  (7) 

При  получении  соотношения  (7)  учтено,  что    и  сделано  предположение,  что  .  Принимая  во  внимание  все  вышеупомянутые  замечания,  приходим  к  следующему  выводу.

Теорема  1.  Оптимальное  управление  в  задаче  (1)-(3)  единственно  и  определяется  из  соотношений

   (8)

где  функция  —  множитель  Лагранжа.

Доказательство.  Необходимое  условие  экстремума  функционала  (4)  —  равенство  нулю  его  первой  вариации.  Такое  условие  будет  выполнено,  если  имеют  место  следующие  соотношения

,  ,  ,

,  .

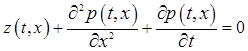Если  к  этим  равенствам  присоединить  еще  условия(3),  то  получим  систему  соотношений  (8).  В  случае  выполнения  равенств  (8)  выражение  (7)  примет  вид

.

При  условии    имеем  .  Это  означает,  что  на  управлении  реализуется  минимум  функционала  (4).  Единственность  оптимального  управления  можно  доказать  с  помощью  таких  рассуждений.  Предположим,  что  существует  еще  одно  оптимальное  управление  .  Тогда  имеет  место  равенство  .  Поскольку  для  обеих  управлений  та    справедливы  соотношения  (8),  то  непосредственно  из  равенства  (7)  имеем  соотношение.  Такое  равенство  возможно  только  в  том  случае,  когда  .  Отсюда  следует,  что  .  Следовательно,  теорема  1  полностью  доказана.

Исследование  системы  уравнений  (8)

Используя  соотношение  ,  для  нахождения  функций  и    получим  следующую  систему  уравнений

.  (9)

Ищем  функции  и  в  следующем  виде

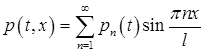  ,.  (10)

Тогда  имеем

  ,  .  (11)

  ,  .  (12)

С  учетом  соотношений  (10)—(12)  вместо  системы  уравнений  (9)  получим  бесконечную  систему  обыкновенных  линейных  дифференциальных  уравнений

   (13)

Если  рассмотреть  матрицу 

 ,  (14)

то  ее  собственные  числа  равны:  ,,  где  .  Им

соответствуют  собственные  векторы    ,    ,

где  .  Поэтому  решение  системы  уравнений  (13),  удовлетворяющее  начальному  условию  ,  ,  будет  таким

.  (15)

Построение  решения  интегро-дифференциального  уравнения  Риккати

Полагая  в  этих  соотношениях  ,  ,  получим

,

.

Принимая  во  внимание  условие  ,  имеем

.

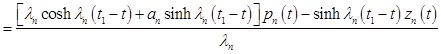Отсюда  непосредственно  находим

.  (16)

Если  ввести  обозначение

,  (17)

то  соотношение  (16)  можно  переписать  так:  .  Легко  проверить,  что  функции    являются  решениями  уравнений

  (18)

и  удовлетворяют  условиям

.  (19)

После  нахождения  функций    рассмотрим  следующее  выражение

.  (20)

Имеют  место  следующие  соотношения

,  (21)

,  (22)

,  (23)

.  (24)

С  учетом  равенств  (21)—(24)  легко  проверить,  что  функция    является  решением  интегро-дифференциального  уравнения  Риккати  с  частными  производными

  (25)

и  удовлетворяет  дополнительным  условиям

,  ,,  ,  .  (26)

Таким  образом,  доказано  следующее  утверждение.

Теорема  2.  Функция  есть  решением  интегро-дифференциального  уравнения  и  удовлетворяет  дополнительным  условиям  (26).

Поскольку  имеют  место  соотношения  ,  ,  то  для  оптимального  управления    получаем  следующую  формулу

,  (27)

где  функция    является  решением  интегро-дифференциального  уравнения

  (28)

и  удовлетворяет  дополнительным  условиям

,  ,  .  (29)

В  результате  этих  рассуждений  приходим  к  следующему  заключению.

Теорема  3.  Если  известна  функция  ,  то  оптимальное  управление    можно  найти  с  помощью  формулы  (27),  в  которой  функция  является  решением  краевой  задачи  (28)—(29).

Список  литературы:

1.Бутковский  А.Г.  Теория  оптимального  управления  системами  с  распределенными  параметрами.  —  М.:  Наука,  1965  —  476  с.

2.Бутковский  А.Г.  Методы  управления  системами  с  распределенными  параметрами.  —  М.:  Наука,  1975  —  568  с.

3.Жуковский  В.И.,  Чикрий  А.А.  Линейно-квадратичные  дифференциальные  игры.  —  Київ:  Наукова  думка,  1994  —  320  с.

4.Лионс  Ж.-Л.  Оптимальное  управление  системами,  описываемыми  уравнениями  с  частными  производными.  —  М.:  Мир,  1972.  —  414  с.

5.Сиразетдинов  Т.К.  Оптимизация  систем  с  распределенными  параметрами.  —  М.:  Наука,  1977  —  480  с.

6.Ройтенберг  Я.Н.  Автоматическое  управление.  —  М.:  Наука,  1971  —  396  с.

7.Donald  E.  Kirk.  Optimal  control  theory.  An  introduction.  —  Dover  Publications,  Inc.,  1998.  —  452  p.

8.Goss  J.D.  Optimal  control  theoretic  methods  for  optimization  and  regulation  of  distributed  parameter  systems.  —  The  university  of  Texas  at  Arlington.  May,  2009.  —  155  p.

9.Naidu  D.S.  Optimal  control  systems.  (Electrical  engineering  textbook  series)  —  CRC  PRESS  —  Boka  Raton  London  —  New  York  —  Washington,  D.  C.  —  2003.  —  433  p.