Статья опубликована в рамках: VIII Международной научно-практической конференции «Физико-математические науки и информационные технологии: проблемы и тенденции развития» (Россия, г. Новосибирск, 26 ноября 2012 г.)
Наука: Информационные технологии
Секция: Методы и системы защиты информации, информационная безопасность
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
ПРИМЕНЕНИЕ ЭЛЛИПТИЧЕСКИХ КРИВЫХ И «ГАММИРОВАНИЯ» ДЛЯ ЗАЩИТЫ ОТ НЕСАНКЦИОНИРОВАННОГО ДОСТУПА
Куржеевский Игорь Владимирович
старший преподаватель, Академия военно-морских сил имени П.С. Нахимова,
г. Севастополь
Бродовская Виолетта Владимировна
студент, Академия военно-морских сил имени П.С. Нахимова,
г. Севастополь
Филимонова Анастасия Викторовна
студент, Академия военно-морских сил имени П.С. Нахимова,
г. Севастополь
E-mail: filay40@yandex.ru
Эллиптические кривые являются одним из основных объектов изучения в современной теории чисел и криптографии. Эллиптическая криптография образует самостоятельный раздел криптографии, посвященный изучению криптосистем на базе эллиптических кривых. В частности, на эллиптических кривых основан российский стандарт цифровой подписи ГОСТ Р 34.10-2001. Под «гаммированием» в данной статье понимается сложение точек эллиптической кривой, соответствующих символам алфавита с точками эллиптической кривой, соответствующих «гамме». «Гамма» — это псевдослучайная последовательность точек эллиптической кривой или точки, соответствующие символам некоторого другого текста.
Эллиптическая кривая — математический объект [3, с. 13], который может быть определен над любым полем и описывается кубическим уравнением следующего вида:
![]()
где c, d, e, f и g являются действительными числами, удовлетворяющими некоторым условиям. Ньютон доказал, что над полем действительных чисел любую эллиптическую кривую можно преобразовать, с помощью замены координат (1) к виду (2) (формула Вейерштрасса).
![]()
![]()
![]() (1)
(1)
![]() (2)
(2)
Чтобы найти точки пересечения эллиптической кривой с осью абсцисс необходимо решить кубическое уравнение с помощью формул Кардано.
![]()
Дискриминант этого уравнения имеет вид:
![]() .
.
Если D<0, то уравнение имеет три различных действительных корня α, β, γ (рисунок 1).
Если D=0, то уравнение имеет три действительных корня, предположим α, β, β, то, по крайней мере, два из них равны (рисунок 2).
Если D>0, то уравнение имеет один действительный корень α и два комплексно сопряженных (рисунок 3).
|
|
|
|
|
Рисунок. 1 D<0 |
Рисунок. 2 D=0 |
Рисунок. 3 D>0 |
Точки эллиптической кривой можно вычитать. Вычитания точек эллиптической кривой реализуется следующим образом (рисунок 4): предположим, что необходимо найти разность точек R и Q. Для этого необходимо отобразить точку R симметрично оси ОХ и получить точку R1. Складывая точки R1 и Q получаем их сумму — точку P1, затем следует отобразить точку P1 симметрично оси ОХ и в результате получаем точку Р, являющуюся разностью точек R и Q.
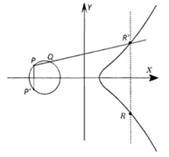
Рисунок. 4. Вычитание точек ЭК
Сложение точек эллиптической кривой равносильно умножению чисел в неэллиптической криптографии (рисунок 5).

Рисунок. 5 Сложение точек ЭК
Сумма двух точек, в свою очередь, также принадлежит эллиптической кривой и имеет координаты, которые вычисляются по следующим формулам:
![]() , если P
, если P![]() Q и
Q и
![]() , если P=Q,
, если P=Q,
где ![]() — угловой коэффициент секущей, а
— угловой коэффициент секущей, а ![]() ,
, ![]() ,
, ![]() ,
, ![]() — координаты точек
— координаты точек
![]()
![]()
![]() .
.
Важное свойство множества точек эллиптической кривой состоит в том, что они образуют абелевую группу. Рассмотрим эллиптическую кривую, заданную над полем вещественных чисел. В этом случае эллиптическая кривая будет представлять собой плоскую кривую и точку O «в бесконечности». Пусть E — эллиптическая кривая над полем вещественных чисел, а P и Q — две точки на E. Определим точки –P и P+Q по приведенным ниже правилам [1, c. 70].
Правило 1. Точки P=(x, y) и −P имеют одинаковые координаты x, а их координаты y различаются только знаком, т. е.−(x, y)=(x,−y) [2, c. 82].
Правило 2. Если P и Q имеют различные координаты x, то прямая l=PQ имеет с E еще в точности одну точку пересечения R кроме двух случаев: когда прямая l оказывается касательной в точке P (тогда полагаем R=P) или касательной в Q (тогда R=Q). Определяем теперь сумму точек P+Q как точку R.
Для реализации алгоритма стохастического шифрования и «гаммирования» с использованием абелевой группы точек эллиптической кривой применяется следующий алгоритм:
1. Для каждого сеанса связи с помощью генератора псевдослучайной последовательности (ГПСП) № 1 с ключом k1 создается новый алфавит с проверкой на уникальность каждого символа, которому соответствует некоторая точка, лежащая на эллиптической кривой.
2. Для каждого сеанса связи с помощью генератора псевдослучайной последовательности (ГПСП) № 1 с ключом k1 создается новый алфавит с проверкой на уникальность каждого символа, которому соответствует некоторая точка, лежащая на эллиптической кривой.
3. Считываем из файла поблочно исходный текст подлежащий шифрованию.
4. Определяем порядковые номера символов блока исходного текста в сгенерированном алфавите.
4.1 Задаем количество случайных символов, которыми будет «разбавлен» блок исходного текста.
4.2 Генерируем случайные символы с помощью ГПСП № 2 с ключом k2 и определяем порядковые номера этих символов в алфавите.
4.3 Создаем одномерный целочисленный массив с длиной равной количеству считанных символов блока исходного текста плюс количество сгенерированных случайных символов. Записываем в массив порядковые номера этих символов в алфавите. Используя ГПСП № 3 с ключом k3, стохастически перемешиваем элементы этого массива.
5. Сгенерированный в пункте 1 алфавит записывается в двухмерный массив.
6. С помощью ГПСП № 4 с ключом k4 осуществляем циклические сдвиги строк и столбцов полученного в предыдущем пункте двухмерного массива, тем самым осуществляем стохастическое перемешивание алфавита для каждого шифруемого символа.
7. Считываем из одномерного массива, полученного в пункте 4.3, порядковый номер в алфавите очередного шифруемого символа и осуществляем замену этого номера на соответствующий порядковый номер из перемешанного в пункте 6 алфавита, таким способом происходит стохастическая замена каждого символа.
8. Производим шифрование, основанное на эллиптической кривой следующим образом:
8.1 Определяем генерирующую точку G эллиптической кривой.
8.2 Генерируем случайное число k.
8.3 Пользователь выбирает в качестве открытого ключа произвольную точку Рв эллиптической кривой, а в качестве секретного ключа некоторое число nв. Уравнение имеет вид:
![]() (9)
(9)
где Рт — точка эллиптической кривой соответствующая шифруемому символу.
9. Считываем из ключевого файла очередной символ «гаммы».
10. Складываем точки эллиптической кривой, соответствующие символу исходного текста и символу «гаммы».
11. Результат шифрования записываем в файл.
Секретным ключом в данной системе шифрования являются символы «гаммы» и ключи генераторов ПСП.
Расшифрование происходит следующим образом:
1. Считываем из соответствующих файлов очередной символ зашифрованного текста и символ гаммы.
2. Находим разность точек эллиптической кривой, соответствующих символу зашифрованного текста и символу гаммы.
3. Применяем следующие уравнение:
![]() (10)
(10)
4. Получив расшифрованные координаты точек ЭК, мы определяем порядковые номера символов, соответствующих этим координатам, то есть символов замены, которые записываем в одномерный массив.
5. Для определения порядковых номеров символов исходного текста и случайных символов осуществляем обратные циклические сдвиги строк и столбцов двухмерного массива, в который записан алфавит. Считываем из одномерного массива, полученного в пункте 4, порядковый номер в алфавите очередного зашифрованного символа и осуществляем его замену на соответствующий порядковый номер из двухмерного массива с алфавитом. Полученные таким образом порядковые номера символов записываются в одномерный массив.
6. С помощью ГПСП № 3 с ключом k3 отбрасываем случайные символы в одномерном массиве из пункта 5 и восстанавливаем первоначальный порядок исходных символов.
Оценим вычислительную стойкость предложенного алгоритма стохастического шифрования с использованием абелевой группы точек эллиптической кривой. Сгенерированный алфавит для каждого сеанса связи содержит 144 символа и включает в себя прописные и строчные буквы латинского алфавита и кириллицы, а также знаки препинания и другие необходимые символы. Если модуль, по которому происходят вычисления, равен, например, р=751, то число точек на данной эллиптической кривой составляет n=727. Общее количество различных алфавитов можно подсчитать по формуле для числа размещений ![]() . Так как n=727, а m=144, то
. Так как n=727, а m=144, то ![]() . Использование циклических сдвигов строк и столбцов двухмерного массива, в который записан сгенерированный алфавит, определяет стохастическое перемешивание элементов этого массива, поэтому любой символ алфавита может быть заменен на любой другой. Если, например, длина исходного теста составляет 1000 символов, то количество возможных вариантов
. Использование циклических сдвигов строк и столбцов двухмерного массива, в который записан сгенерированный алфавит, определяет стохастическое перемешивание элементов этого массива, поэтому любой символ алфавита может быть заменен на любой другой. Если, например, длина исходного теста составляет 1000 символов, то количество возможных вариантов ![]() , что составляет примерно 102158. Для несанкционированного доступа к информации злоумышленнику необходимо определить также, какие из расшифрованных символов являются случайными, а затем отбросить эти случайные символы и восстановить первоначальный порядок следования в тексте исходных символов.
, что составляет примерно 102158. Для несанкционированного доступа к информации злоумышленнику необходимо определить также, какие из расшифрованных символов являются случайными, а затем отбросить эти случайные символы и восстановить первоначальный порядок следования в тексте исходных символов.
Выводы. Предложенный алгоритм стохастического шифрования с использованием абелевой группы точек эллиптической кривой отличается от существующих алгоритмов тем, что для каждого сеанса связи генерируется новый уникальный алфавит, в котором каждому символу алфавита соответствуют координаты некоторой точки на эллиптической кривой; затем исходный текст дополняется случайно сгенерированными символами и с помощью генератора псевдослучайных последовательностей происходит их стохастическое перемешивание, далее происходит стохастическая замена каждого символа, который шифруется с использованием случайного параметра. Стохастическое преобразование исходной информации, подлежащей защите от несанкционированного доступа, позволяет повысить криптостойкость от взлома методом полного перебора. Данный алгоритм был реализован в среде Aribasw и С# (SHARP), успешно прошел тестирование на правильность результатов шифрования и расшифрования и может быть использован для защиты информации от несанкционированного доступа.
Список литературы:
1.Болотов A.A,. Гашков С.Б, Фролов А.Б., Часовский A.A.. Алгоритмические основы эллиптической криптографии / — М.: Изд-во РГСУ, 2004. — 499 с.
2.Ростовцев А.Г. Теоретическая криптография / А.Г. Ростовцев, Е.Б. Маховенко. — Санкт-Петербург: AHO НПО "Профессионал", 2004. — 464 с.
3.Державний стандарт України. Інформаційні технології. Криптографичний захист інформації. Цифровий підпис, що ґрунтується на еліптичних кривих. Формування та перевірка. ДСТУ 4145-2002. Видання офіційно. Київ. Держстандарт України. 2003.
дипломов




Оставить комментарий