ДИФФЕРЕНЦИАЛЬНОЕ СЕЧЕНИЕ УГЛОВОГО НЕУПРУГОГО РАССЕЯНИЯ ПО ТЕОРИИ ГРИЗИНСКОГО

Чан Хай Кат

Магистрант, ВолгГТУ, г. Волгоград

E-mail: tranhaicat@hotmail.com

В данной работе дифференциальное сечение углового рассеяния при неупругих соударениях вычислено по полуклассической нерелятивистской теории Гризинского.

Ключевые слова: дифференциальное сечение, упругое рассеяние, неупругое рассеяние, угловое рассеяние, ионизация

Для сечения ионизации атома при взаимодействии с налетающим электроном было предложено несколько выражений. Наиболее широкое применение получила полуклассическая нерелятивистская формула Гризинского [5] для дифференциального сечения однократной ионизации атома электроном с энергией , которая сопровождается потерей энергии , то есть вероятности того, что при единичной плотности потока (за 1 секунду единичную площадку пересекает один электрон) этот электрон столкнется с одним атомом, расположенным в некоторой точке этой площадки, и при этом произойдёт однократная ионизация атома, т. е. будет выбит один из  электронов, находящихся на -той оболочке атома с энергией связи  и ему будет сообщена некоторая кинетическая энергия, так что потеря энергии столкнувшегося с атомом электрона составит величину

                                                             1

Здесь суммирование ведётся по всем оболочкам атома, для которых выполняется неравенство . Предложенная Гризинским формула для вычисления этого дифференциального сечения однократной ионизации -той оболочки атома имеет вид [5]

                                           2

При ионизации -той оболочки, минимальная потерянная энергия электрона  равна , а максимальная потерянная энергия  равна  в силу неразличимости электронов падающего на атом и выбитого из него в результате ионизации.

Рисунок 1. Схема неупругого рассеяния электрона на атоме:  - импульс падающего электрона,  - импульс рассеянного электрона,  - переданный импульс

На рисунке 1 показана схема неупругого рассеяния электрона на атоме. При неупругом рассеянии справедлив закон сохранения импульса. Применяя теорему косинусов, имеем

где  - импульс падающего электрона,  - импульс рассеянного электрона. Используя формулу  и учитывая, что , получаем

Выполнив простые преобразования, получим

                                                                                               5

Потерянная энергия должна удовлетворять неравенству

                                                                                             6

Из и после элементарных преобразований получаем пределы, в которых находится угол между направлениями падающего и рассеянного электрона

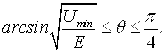
По определению дифференциального сечения углового рассеяния

                                                                                         7

где  - даётся формулами Гризинского и .

Из получаем

                                                                                     8

В сферической системе координат

В случае цилиндрической симметрии рассеяние происходит в элемент телесного угла

                                                                                         9

Подставив и в , получим

                                                                                   10

Дифференциальное сечение углового рассеяния при неупругих столкновениях вычисляется по формуле и показывается на рисунке 2.

Чтобы оценивать вероятность отклонения электронов из-за неупругих соударений, мы вводим дифференциальное сечение электронного пучка при упругом рассеянии, вычисленном Моттом на основе решения уравнения Дирака, даются выражением [1]

                                                                                        11

где амплитуды рассеяния  и  определяются в работах [3] и [4]

На рисунке 2 мы вводим ещё упругое дифференциальное сечение , которые вычислены по формуле и зависят от полярного угла рассеяния . Видно, что угловое рассеяние при неупругих столкновениях становится существенным при энергиях электронов меньших сотен эВ.

Рисунок 2. Сечения рассеяния электрона с энергией 100 эВ, 1000 эВ и 10 кэВ на атомах Si и Ge: сплошная линия - угловое рассеяние при неупругих столкновениях по Гризинскому, штриховая линия - угловое рассеяние при упругих столкновениях по Мотту

Список литературы:

1. Н. Теория атомных столкновений / Н. Мотт, Г. Месси; ред. Я. И. Френкеля — Пер. со 2-ого англ-ого изд. Т. А. Конторовой — М.: Иностранная Литература, 1965. — 752 с.

2. М. В. Исследование численного моделирования на основе метода Монте-Карло для исследования и оптимизации процессов высокоэнергетической электронной литографии: дис. … канд. физ. - мат. наук / А. В. Силаков. — М., 2003. — 151 с.

3.Упругое рассеяние электронов в твёрдых телах / В. А. Смоляр, Чыонг Тхань Хиеу Нгуен // Изв. ВолгГТУ. Серия «Электроника, измерительная техника, радиотехника и связь». Вып. 5: межвуз сб. науч. ст. / ВолгГТУ. — Волгоград, 2011. — № 6. С. 15 — 19.

4. M. Elastic scattering calculations for electrons and positrons in solid targets / M. Dapor // J. Appl. Phys. — 1996. — V. 79, N. 11. — P. 1—6.

5. M. Two-particle collisions. II. Coulomb collisions in the laboratory system of coordinates / M. Gryzinsky // Phys. Rev. — 1965. — V. 138. — № 2A. — P. 322 — 335.