Статья опубликована в рамках: VIII Международной научно-практической конференции «Научные достижения биологии, химии, физики» (Россия, г. Новосибирск, 06 июня 2012 г.)
Наука: Физика
Секция: Акустика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
ТОЧНЫЕ РЕШЕНИЯ РАСПРОСТРАНЕНИЯ ЗВУКА МЕТОДОМ ВИНЕРА-ХОПФА
Хлопков Юрий Иванович
д-р физ.-мат. наук, профессор МФТИ, г. Жуковский
Email:
Жаров Владимир Алексеевич
канд. физ.-мат. наук, доцент МФТИ, г. Жуковский
Email:
Чернышев Сергей Леонидович.
д-р физ.-мат. наук, директор ЦАГИ, г. Жуковский
Зея Мьо Мьинт
канд. физ.-мат. наук, докторант, МФТИ, г. Жуковский
Email: zayyarmyomyint@gmail.com
1. Введение
В связи с развитием гражданской авиации, ужесточением требований ИКАО по шуму, созданием авиадвигателя V-го поколения задача снижение шума силовой установкой становится одной из наиболее актуальных проблем современной аэрофизики. Для того чтобы уменьшить излучаемый авиационным двигателем шум до приемлемого уровня, должны быть, по крайней мере, разработаны специальные методы подавления шума струи, основным источником которого являются сложные вихревые элементы течения. Для разработки подобных методов необходимо глубокое понимание процессов, происходящих в неоднородных и нестационарных струйных течениях. Одним из важнейших инструментов исследований в этом направлении является численное моделирование. Ниже перечисляются наиболее значимые проблемы, возникающие из специфики задач аэроакустики.
а) Аэроакустические задачи являются по определению задачами нестационарными. При этом в отличие от задач традиционной аэродинамики, для которых нестационарность или отсутствует вовсе или является низкочастотной, в аэроакустических задачах нестационарность имеет место в широком частотном диапазоне. В частности при численном разрешении задач излучения и распространения звука необходимо иметь дело с волнами высоких частот, что создает серьезные препятствия для точных расчетов.
б) Акустические волны, генерируемые нестационарным потоком, имеют очень малую амплитуду по сравнению с величинами, характеризующими основной поток. Наиболее часто встречающаяся ситуация – скорость в звуковой волне на пять–шесть порядков меньше скорости основного течения. Поэтому для корректных расчетов шума, излучаемого турбулентными течениями, необходимо применять численные алгоритмы с чрезвычайно низким численным шумом.
в) В большинстве аэроакустических задач интерес представляют звуковые волны, излучаемые в дальнее поле. Эта особенность выдвигает требование поиска однородно справедливых решений во всей расчетной области (от места расположения источника звука до места расположения точки наблюдения). Поэтому для корректного описания задач распространения звука численные схемы должны обладать минимальными численными дисперсией и диссипацией. Кроме этого, звуковые волны должны распространяться с правильной скоростью звука в любом направлении независимо от ориентации расчетной сетки.
г) В задачах традиционной аэродинамики возмущения в потоке обычно сильно затухают вдали от области, в которой они создаются. Напротив, акустические волны затухают довольно медленно, и поэтому достигают границ расчетной области, имея конечные амплитуды. Тем самым, в задачах аэроакустики остро стоит проблема граничных условий на границе расчетной области. Такие граничные условия призваны не допустить отражения акустических волн, приходящих на границу расчетной области, обратно внутрь расчетной области. Решение данной проблемы является крайне важной составляющей любого численного метода в аэроакустике, так как иначе численный расчет дает существенно неверные результаты. В самом деле, нестационарные течения, излучающие звук обычно являются неустойчивыми. Приход в область излучения артефактных возмущений, отраженных от границ расчетной области, вызывает накачку неустойчивостей, приводящую при длительном расчете к автоколебательным режимам, которые могли быть изначально не присущи исследуемому явлению.
д) Аэроакустические задачи являются задачами со многими весьма различными пространственно-временными масштабами. При этом пространственные масштабы длин, определяющие турбулентное течение в области акустического источника, существенно отличаются от длин волн, которые они генерируют в дальнее поле. Поэтому, во-первых, любой численный метод, применяемый для решения задачи генерации звука турбулентными потоками, должен обладать способностью разрешать существенно различные масштабы длин в разных областях расчетной области. Во-вторых, только малая часть пульсационной составляющей потока в ближнем поле оказывается переизлучаемой в дальнее поле. Как известно, для эффективного излучения звука пространственно-временные масштабы источника должны соответствовать излучающей сфере в Фурье-пространстве волновых чисел. Обычно Фурье-образы наиболее энергонесущих пульсаций в области источника лежат далеко от излучающей сферы и не излучают звук, т. е. звук может излучаться ничтожной в энергетическом смысле частью турбулентного потока, попадающей, однако, на излучающую сферу. Кроме того, динамика турбулентного потока является существенно нелинейной, и тем самым, характеризующаяся нелинейным взаимодействием сразу всех пространственно-временных масштабов. Поэтому для корректного описания излучающих масштабов необходимо корректно разрешать в области источника сразу все пространственно-временные масштабы.
Перечисленный, далеко не полный, список проблем аэроакустики подчеркивает чрезвычайную важность наличия некоего эталона, на котором бы тестировались разрабатываемые численные методики. Наиболее надежным эталоном может быть точное решение о распространении звука в постановке близкой к рассматриваемой проблеме. Ниже представлены точные решения задачи об излучении звука из плоского канала методом Винера-Хопфа.
2. Точные решения задачи распространения звука от плоского канала
2.1 Постановка задачи
Линеаризованные относительно однородного состояния газа с (p0, r0, Q0, v0) уравнения Эйлера, где p0, r0, Q0, v0 = 0, соответственно давление, плотность, температура и скорость, ![]() - приращения этих величин, с учетом уравнения энергии и уравнения состояния (p = rRQ) приводятся к уравнениям относительно плотности и скорости:
- приращения этих величин, с учетом уравнения энергии и уравнения состояния (p = rRQ) приводятся к уравнениям относительно плотности и скорости:
![]()
где ![]() - квадрат скорости звука в невозмущенном газе.
- квадрат скорости звука в невозмущенном газе.
Введем безразмерные величины
![]()
и безразмерные независимые переменные
![]()
Тогда линеаризованные уравнения можно записать
![]()
Из этих уравнений подстановкой одно в другое можно получить волновое уравнение, например, относительно ![]() :
:
![]()
Линейную задачу удобно решать в комплексном виде. Для этого сделаем замену ![]()
Действительная часть от ![]() (
(![]() ) дает пространственное распределение плотности, а функция
) дает пространственное распределение плотности, а функция ![]() удовлетворяет уравнению Гельмгольца
удовлетворяет уравнению Гельмгольца
![]()
Поскольку в, конечном счете, речь будет идти о численном методе сквозного счета, то необходимо указать соответствие между результатами, получаемыми в этих методах, и решением линейной задачи в случае малых амплитуд возмущений. Легко показать, что это соответствие устанавливается соотношением
![]()
где ![]() - соответственно действительные плотность и вектор скорости газа.
- соответственно действительные плотность и вектор скорости газа.
2.2 Результаты решения
Рассмотрим следующую задачу для уравнения Гельмогольца
![]()
с граничными условиями на полуплоскостях при ![]() (см. Рис.1)
(см. Рис.1)
![]()
и нулевыми граничными условиями при ![]() вне канала. При этом стенки канала простираются вдоль оси
вне канала. При этом стенки канала простираются вдоль оси ![]() от
от ![]() до 0.
до 0.
Внутри канала входящая волна имеет вид
![]()
Для чётного ![]() решение задачи можно записать в виде [2]
решение задачи можно записать в виде [2]

при ![]()

при ![]() .
.
где
![]()
![]() ,
,
![]() , С – константа Эйлера.
, С – константа Эйлера.
Ветви аргумента комплексного числа были определены в соответствии с определениями монографии [2].
При N=0, x<0, -1<y<1 получаем решение в виде
![]()
где ![]() - совокупность гармоник, отраженных от края и затухающих вглубь канала. Выражение для
- совокупность гармоник, отраженных от края и затухающих вглубь канала. Выражение для ![]() при
при ![]() имеет вид (с учетом 20 гармоник)
имеет вид (с учетом 20 гармоник)
![]()
Таблица. 1.
Значения коэффициентов гармоник ![]()
n |
ln |
-bn |
n |
ln |
bn |
1 |
2.978188 |
0.011025 - 0.134641 i |
2 |
6.203097 |
0.001825 - 0.045553 i |
3 |
9.371576 |
0.000654 -0.024597 i |
4 |
12.526519 |
0.000317 - 0.015926 i |
5 |
15.6761 |
0.000181 -0.011375 i |
6 |
18.823011 |
0.000115 -0.008643 i |
7 |
21.968400 |
0.000078 -0.006851 I |
8 |
25.112839 |
0.000056 - 0.005601 i |
9 |
28.256644 |
0.000041 - 0.004689 i |
10 |
31.400007 |
0.000032 - 0.003999 i |
11 |
34.543048 |
0.000025 -0.003462 I |
12 |
37.685846 |
0.000020 - 0.003035 i |
13 |
40.82846 |
0.000016 - 0.002688 i |
14 |
43.970927 |
0.000014- 0.00240 i |
15 |
47.113278 |
0.000011-0.002162 I |
16 |
50.255534 |
-0.001786 i |
17 |
53.397712 |
-0.001786 I |
18 |
56.539825 |
-0.001637 i |
19 |
59.681883 |
-0.001506 i |
20 |
62.823895 |
-0..001392 i |
a =-0.917658 - 0.793380 i |
|||||
Здесь ![]() - действительные корни уравнения
- действительные корни уравнения ![]() .
.
Коэффициент отражения определяется выражением
![]()
![]()
где С – постоянная Эйлера, и в рассмотренном случае равен (![]() полагается равной 1)
полагается равной 1)
![]()
В дальней зоне (x >>1, y >>1) решение имеет вид
![]()
Величина ![]() определяет диаграмму направленности излучателя. Согласно общей теории [1] поток энергии в дальней зоне определяется выражением
определяет диаграмму направленности излучателя. Согласно общей теории [1] поток энергии в дальней зоне определяется выражением
![]()
где ![]() - среднее по времени от произведения радиальной компоненты пульсаций скорости на пульсации давления,
- среднее по времени от произведения радиальной компоненты пульсаций скорости на пульсации давления, ![]() - единичный вектор в направлении излучения. Воспользуемся комплексным решением для определения радиальной компоненты скорости:
- единичный вектор в направлении излучения. Воспользуемся комплексным решением для определения радиальной компоненты скорости:
![]()
Дифференцируя выражение для плотности в дальней зоне по ![]() и оставляя только члены пропорциональные
и оставляя только члены пропорциональные ![]() , получим
, получим
![]()
В результате, умножая на ![]() , получаем диаграмму направленности
, получаем диаграмму направленности
![]()
На рис. 2 приведена зависимость числа незатухающих типов волн в канале с ![]() в зависимости от волнового числа падающей волны
в зависимости от волнового числа падающей волны ![]() .
.

Рис. 1. Схема канала

Рис. 2. Число незатухающих гармоник
На рис. (3—7) приведены результаты расчетов для модуля коэффициента отражения, его фазы, диаграммы направленности для ![]() , а также поле флуктуаций давления внутри канала для
, а также поле флуктуаций давления внутри канала для ![]() . Диапазон
. Диапазон ![]() выбран из условия того, что внутри канала все гармоники, возникающие из-за отражения падающей волны от края канала, затухают внутри канала и, таким образом, на некотором расстоянии от края канала имеются только одна падающая и одна отраженная волна.
выбран из условия того, что внутри канала все гармоники, возникающие из-за отражения падающей волны от края канала, затухают внутри канала и, таким образом, на некотором расстоянии от края канала имеются только одна падающая и одна отраженная волна.

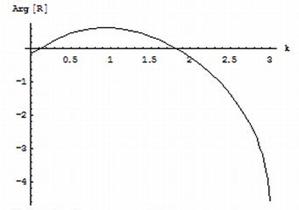
|
Рис. 3. Модуль коэффициента отражения |
Рис. 4. Фаза коэффициента отражения отражения |

Рис. 5. Диаграмма направленности акустического поля для трех значений
На рис. (8-11) представлено распределение давления (плотности) в окрестности края канала (x = 0) и вне его в полосе –1 < y < 1. Решение составлено из двух кусков при 0 >x > -2 и x > 2. Точность решений в этих областях несколько различается. Этим объясняется некоторая нестыковка на линии {x = 0, -1 < y < 1}. Избранный способ интегрирования не позволил получить поле в точках с y=![]() . Поэтому области изображения акустических полей несколько различны.
. Поэтому области изображения акустических полей несколько различны.

Рис. 6. Акустическое поле вблизи края канала

Рис. 7. Акустическое поле в канале

Рис. 8. Акустическое поле давления в окрестности края канала.

Рис. 9. Распределение давления (плотности) на оси канала.

Рис. 10. Распределение давления (плотности) вне канала в полосе –1<y<1 при 20>x>-2

Рис. 11. Распределение давления (плотности) во всей области
2.3 Волноводные моды плоской струи (Рис. 12)
В этом случае уравнения распространения волн имеют вид
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Детерминант этих уравнений
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
где


![]()
Равенство нулю этого детерминанта определяет дискретные волноводные моды струи. Из этого условия имеем две серии стандартных волноводных мод
![]()
Особый интерес представляет дискретные моды определяемые полиномом шестой степени. Среди этих мод содержатся моды соответствующие неустойчивости сдвиговых слоев, а также моды не затухающие на бесконечности.
![]()
![]()
![]()
![]()
![]()
![]() .
.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Рис. 12. Схема истечения плоской струи
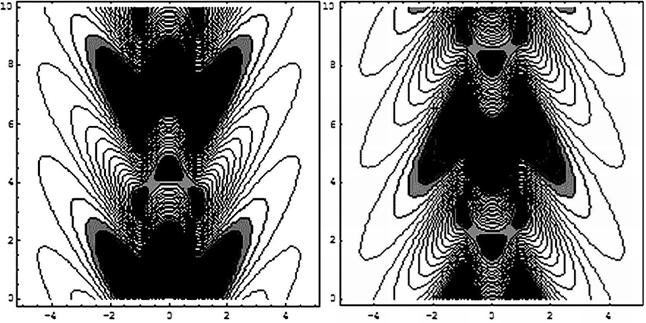
Рис. 13. Линии уровня звукового давления. Моды № 1,2

Рис. 14. Линии уровня звукового давления. Моды № 3,4
На рис. 13, 14 представлено геометрическое изображение мод (линии уровня звукового давления). Моды № 1,2,3,4 соответственно.
Все результаты получены с помощью пакета Mathematica 5.0 [3, 4]
Заключение
В работе представлен перечень важнейших проблем определения шума в струйных течениях. Решение этих проблем требуют специальных численных методик и больших вычислительных ресурсов. При этом не гарантируется, что все акустические явления попадут в круг решаемых проблем. В этой связи многократно возрастает значение эталонного решения, на котором можно тестировать разрабатываемые сложные численные методики. Кроме того, наряду с этими сложными методиками всегда полезно иметь под рукой простой способ качественной и количественной оценки возможных явлений дающих наибольший вклад в решаемую проблему. Метод выделения особенностей представляется авторам наиболее приемлемым для определения шума струйных течений. По этим причинам получено точное решение линейной задачи об излучении звука из плоского канала методом Винера-Хопфа (подобные решения можно получить и для круглой трубы).
Список литературы:
1.Ландау Л.Д., Лифшиц Е.М. Теоретическая физика // Гидродинамика. — М.: Наука. – 1986. – T. 6. – 736 c.
2.Нобл Б. Метод Винера-Хопфа. — М.: Иностранная литература. – 1962. - 279 с.
3.Хлопков Ю.И., Жаров В.А., Горелов С.Л. Руководство по компьютерной аналитике. — М.: МФТИ. – 2000. – 117 c.
4.Mathematica 5.0. Users Guide, Wolfram Research. – 2003.
дипломов

Оставить комментарий