Статья опубликована в рамках: VIII Международной научно-практической конференции «Научные достижения биологии, химии, физики» (Россия, г. Новосибирск, 06 июня 2012 г.)
Наука: Физика
Секция: Механика жидкости, газа и плазмы
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
ИССЛЕДОВАНИЕ АЭРОДИНАМИКИ ПЕРСПЕКТИВНЫХ ГИПЕРЗВУКОВЫХ ЛЕТАТЕЛЬНЫХ АППАРАТОВ
Хлопков Юрий Иванович
д-р физ.-мат. наук, профессор МФТИ, г. Жуковский
Email: khlopkov@falt.ru
Зея Мьо Мьинт
канд. физ.-мат. наук, докторант, МФТИ, г. Жуковский
Email: zayyarmyomyint@gmail.com
Хлопков Антон Юрьевич
спирант, МФТИ, г. Жуковский
Чжо Зин
аспирант, МФТИ, г. Жуковский
Email: kyawzin.mipt@gmail.com
Засыпалов Валерий Васильевич
канд. техн. наук, доцент МФТИ, г. Жуковский
Email: zasypalov@falt.ru
Технический прогресс в космической технике и гиперзвуковой авиации привел к интенсивному развитию теоретических и экспериментальных исследований в области аэродинамики гиперзвуковых течений. Компьютерное моделирование позволяет при помощи инженерных методов быстро и надежно проводить анализ аэродинамических характеристик летательных аппаратов. При этом важное значение имеет исследование двух предельных областей газовой динамики. Одна из них - изучение динамики сплошной среды, а другая – свободномолекулярная газовая динамика и примыкающая к ней среда, где течение газа является разреженным [8]. Направление исследования гиперзвукового обтекания тел разреженном газом можно определить так: в первом случае в рамках обычной теории газовой динамики учитывают явления скольжения на поверхности обтекаемого тела, которое пропорционально разреженности среды, а второе, исходя из известной теории свободномолекулярного потока, пытаются учесть влияние межмолекулярных столкновений на аэродинамические характеристики [4].
Трудность экспериментального исследования аэродинамики гиперзвуковых летательных аппаратов (ГЛА) обуславливается воспроизведением натурных условий полета в аэродинамических трубах. Моделирование высокоскоростных течений предполагает соблюдение критериев подобия, в первую очередь по числам Маха, Рейнольдса и отношением температур набегающего потока и температуры поверхности, а также обеспечением низкой степени турбулентности и однородности потока в рабочей части установки. При моделировании натурных условий основного критерия подобия Рейнольдса необходимо выдерживать целый ряд других критериев подобия. Одновременное решение этих проблем в рамках одной экспериментальной установки представляется невозможным. Законы поведения аэродинамических характеристик в переходной области весьма сложны и не могут быть получены простой интерполяцией данных для сплошной среды и свободномолекулярных течений [4]. Исследование течений газа в переходной области между течениями сплошной среды и свободномолекулярным представляет собой достаточно сложную задачу. Сложность обусловлена тем, что описание этих течений выходит за рамки обычной газовой динамики и требует учета молекулярной структуры газа для чего необходимо решать уравнение Больцмана. Решение уравнения Больцмана при малых числах Кнудсена, особенно для сложных тел - задача чрезвычайно трудоемкая. В этой связи естественным является появление и развитие инженерных методов, обоснованных совокупным материалом экспериментальных, теоретических, численных результатов, дающих возможность предсказания аэродинамических характеристик (АДХ) сложных тел в переходном режиме. Метод основан на так называемой гипотезе локальности, предполагающей, что поток импульса на элемент поверхности определяется местным углом его наклона к набегающему потоку. Обработка экспериментальных данных показывает, что точность теории локального взаимодействия вполне приемлема для инженерных расчетов аэродинамических характеристик широкого класса тел на этапе предварительного проектирования [1].
Целью настоящей работы является создание в применении инженерной программы определения основных аэродинамических характеристик сложной формы тел. Программа удобна для учета влияния числа Re в различных модификациях моделей локальности, предусматривает простой метод задания формы тела. Проведены аэродинамические расчеты воздушно-космического аппарата (ВКА) типов «Клипер (Clipper), модель ЦАГИ» и ГЛА «Сокол (Falcon HTV-2)» в разреженной атмосфере с помощью метода, основанного на гипотезе локальности при различных числах Re.
Трудности решения аэродинамических задач обтекания пространственных тел потоком разреженного газа вызвали развитие инженерных полуэмпирических методов, использующих накопленные теоретические, экспериментальные и расчетные данные. При моделировании натурных условий необходимо учитывать влияние основных критериев подобия. В условиях гиперзвуковой стабилизации более рационально использовать в качестве критерия разреженности не число Кнудсена, а число Рейнольдса.
В данной работе используются выражения для элементарных сил давления и трения в форме работы [3].
![]() ,
,
![]() .
.
Здесь коэффициенты p0, p1, t0 (коэффициенты режима течения) зависят от числа Рейнольдса Re0 = r¥V¥L/m0, в котором коэффициент вязкости m0 вычисляется при температуре торможения T0. Кроме числа Рейнольдса наиболее важным параметром является температурный фактор tw = Tw/T0, где T0, Tw – температура торможения и температура поверхности.
Зависимость коэффициентов режима в гиперзвуковом случае должна обеспечивать переход к свободномолекулярным значениям при Re0→0 и значением теории Ньютона, методов тонких касательных клиньев или конусов при Re0→∞. На основе анализа расчетных и экспериментальных данных предложены эмпирические формулы
![]() ,
, ![]() ,
,
![]() .
.
Здесь
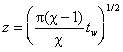 ,
, ![]() ,
,
![]() ,
, ![]() .
.
где h – относительный поперечный размер аппарата, равный отношению его высоты к длине.
Предложенная методика хорошо зарекомендовала себя для расчета гиперзвукового обтекания выпуклых не очень тонких пространственных тел. Расчет полностью отражает качественное поведение Сx в зависимости от разреженности среды во всем диапазоне углов атаки и дает количественное соответствие с точностью около 5 % [6, 7].
Локальный метод расчета аэродинамических характеристик тел в гиперзвуковом потоке разреженного газа в переходном режиме дает хороший результат по Cх для широкого класса тел. При малых углах атаки (a < 5°) точность результата ухудшается, в этом случае необходимо привлекать более полные модели, учитывающие наличие пограничного слоя [6, 7].
Представлены результаты расчета коэффициентов силы сопротивления для гиперзвуковых летательных аппаратов вариантов «ВКА Клипер ЦАГИ (Clipper) [2, 5]» (Рис. 1, 2) и «Сокол (Falcon HTV-2)» (Рис. 3, 4). Расчеты проводились с использованием локального метода в диапазоне углов атаки a от 0° до 90° с шагом 5°. Параметры задачи были следующие: отношение теплоемкостей g = 1.4; температурный фактор tw = Tw/T0 = 0.1; число Рейнольдса Rе0 = 0, 10, 102, 104.

Рис. 1. Космический аппарат «Клипер» и быстроходныйчайный корабль «Clipper»

Рис. 2. Геометрическое представление варианта «ВКА Клипер, модель ЦАГИ»

Рис. 3. Гиперзвуковой летательный аппарат «(Falcon HTV-2)» и
Сокол (Falcon)

Рис. 4. Геометрическое представление варианта «Falcon HTV-2»

Рис. 5. Зависимость Cx(a) для «Клипер» и «Falcon HTV-2» (tw = 0.1)
Для примера на рис. 5 представлено сравнение результатов расчета аэродинамических характеристик гиперзвуковых летательных аппаратов «Клипер» и «Falcon HTV-2» в переходном режиме при различных значениях числа Рейнольдса Re0, т. е. на различных высотах полета. Из этих результатов видно, что коэффициенты силы сопротивления Falcon HTV-2 меньше, чем у Клипера. Но для конечного заключения в пользу того или иного проекта необходимо провести комплексное многопараметрическое исследование.
Список литературы:
1.Алексеева Е.В., Баранцев Р.Г. Локальный метод аэродинамического расчета в разреженном газе. — Изд. ЛГУ, 1976.
2.Ваганов А.В., Дроздов С.М., Косых А.П., Нерсесов Г.Г., Челышева И.Ф., Юмашев В.Л. Численное моделирование аэродинамики крылатого возвращаемого космического аппарата // Ученые записки ЦАГИ. 2009. Т. XL, № 2, С. 3—15.
3.Галкин В.С., Ерофеев А.И., Толстых А.И. Приближенный метод расчета аэродинамических характеристик тел в гиперзвуковом разреженном газе // Труды ЦАГИ. 1977. Вып. 1833.
4.Гусев В.Н., Коган М.Н., Перепухов В.А. О подобии и изменении аэродинамических характеристик в переходной области при гиперзвуковых скоростях потока // Ученые записки ЦАГИ, Том 1, № 1, 1970. С. 24—33.
5.Зея Мьо Мьинт, Хлопков А.Ю. Аэродинамические характеристики летательного аппарата сложной формы с учётом потенциала взаимодействия молекулярного потока с поверхностью // Ученые записки ЦАГИ. 2010, Т. XLI, № 5, С. 33—45.
6.Хлопков Ю.И. Статистическое моделирование в вычислительной аэродинамике. М., МФТИ, 2006, 160 с. (монография)
7.Belotserkovskii O.M., Khlopkov Y.I. Monte Carlo Methods in Mechanics of Fluid and Gas. World Scientific Publishing Co. N-Y, London, Singapore, Beijing, Hong Kong 2010, 268 p. (monograph)
8.Kogan M.N. Kinetic theory in aerothermodynamics. Progress in Aerospace Sciences. 1992. Т. 29. № 4. С. 271.
дипломов

Оставить комментарий