Статья опубликована в рамках: XII Международной научно-практической конференции «Естественные и математические науки в современном мире» (Россия, г. Новосибирск, 11 ноября 2013 г.)
Наука: Науки о Земле
Секция: Картография и геоинформатика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
ВЕКТОРНОЕ РЕШЕНИЕ ОБРАТНОЙ ГЕОДЕЗИЧЕСКОЙ ЗАДАЧИ НА БОЛЬШИЕ РАССТОЯНИЯ
Даренская Людмила Васильевна
инженер, Инженерно-технологическая академия (ТРТИ), Федеральное государственное автономное образовательное учреждение высшего профессионального образования «Южный федеральный университет», г. Таганрог
THE VECTOR SOLUTION OF THE INVERSE GEODETIC PROBLEM FOR GREAT-CIRCLE DISTANCES
Ludmila Darenskaya
engineer, The Engineering-Technological Academy in the Southern Federal University (SFedU), Taganrog
АННОТАЦИЯ
В статье излагается векторный метод решения обратной геодезической задачи на большие расстояния, основой которого является геометрия Лобачевского. Решение было получено 160 лет спустя после опубликованного метода Бесселя, который являлся прежде единственным, хотя были многочисленные попытки найти другое решение.
ABSTRACT
The vector method of a solution of the inverse geodetic problem for great-circle distances which is based on the hyperbolic geometry (also called Bolyai-Lobachevskian geometry) is considered. The solution was obtained 160 years later after the published Bessel method which was the only way of the solution before though there were numerous attempts to find other solution.
Ключевые слова: обратная геодезическая задача (ОГЗ) на большие расстояния; векторный метод решения; геометрия Лобачевского; метод Бесселя.
Keywords: inverse solution of a geodetic problem for great-circle distances; vector method; Bolyai-Lobachevskian geometry; Bessel method.
Основой решения прямой геодезической задачи (ПГЗ) и обратной геодезической задачи (ОГЗ) на большие расстояния является система дифференциальных уравнений (1):
 (1)
(1)
![]()
где: A — азимут;
A1 — прямой азимут;
A2 — обратный азимут;
L — долгота,
B — широта;
s — длина геодезической линии;
c — const
Запишем условия задач.
ПГЗ — дано: A1, B1, L1, s; найти: A2, B2, L2.
ОГЗ — дано: B1, L1, B2, L2; найти: A1, A2, s.
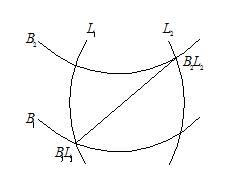
Рисунок 1. Графическое условие задачи
Решение ПГЗ можно свести к численному интегрированию системы дифференциальных уравнений (1) на вычислителе.
ОГЗ является более сложной задачей. Неизвестная функция s является аргументом, эллиптические интегралы, содержащие её, не выражаются через элементарные функции. Решается ОГЗ методом Бесселя [3, с. 289], который заключается в следующем: делается отображение с эллипсоида на сферу, решается задача, а затем обратный переход, используется разложение функции в ряд.
В данной работе предлагается векторный метод [1], [2], полученный 160 лет спустя после опубликованного метода Бесселя, который являлся единственным, хотя были многочисленные попытки найти другое решение [4, с. 51].
Векторный метод позволяет свести решение обратной геодезической задачи к численному интегрированию системы дифференциальных уравнений, аналогично решению прямой геодезической задачи. Сфера не используется, решение на эллипсоиде.
В этом методе применяется геометрия Лобачевского, в отличие от общепринятой геометрии Евклида. Поверхность эллипсоида рассматривается как криволинейное пространство, геодезическая линия на ней — как криволинейный вектор в этом пространстве.
Возьмём в качестве начального вектора дугу меридиана, проходящую через точку (B1, L1) и ограниченную параллелью B2. Фиксируя точку (B1, L1), будем поворачивать вектор таким образом, чтобы конец его двигался по параллели B2 в сторону точки (B2, L2) до тех пор, пока не попадёт в эту точку. Параметры полученной геодезической линии и будут решением обратной геодезической задачи.

Рисунок 2. Графическое изображение векторное решения
Составим уравнения движения вектора. Для этого используем известные дифференциальные формулы 1-го ряда, которые описывают изменения (d) параметров геодезической линии при её малом смещении [3, с. 146]. Эти формулы не являются уравнениями. Запишем их в общем виде:
![]()
где F = F(A, B, m) Ф1=s; Ф2=A1; Ф3= A2; (2)
m — приведённая длина геодезической линии
В нашем случае точка (B1, L1) и параллель B2 фиксированы, поэтому их изменения (d) равны нулю, т.е. dB1 = dL1 = dB2 = 0. Будем рассматривать малое смещение геодезической линии как бесконечное малое, т. е. дифференциалом. Тогда получим систему дифференциальных уравнений, решением которой и будет решение обратной геодезической задачи.
 (3)
(3)
![]()
где: s0 и m0 — длина и приведённая длина дуги меридиана
При составлении этих уравнений дифференцирование идёт по долготе L при повороте геодезической линии. Для уравнений (1) /геометрия Евклида/ дифференцирование идёт по неподвижной геодезической линии.
Система уравнений (3) имеет аналитическое решение. Эллиптические интегралы s0 и m0 входят только в начальные условия [2, с. 66]. Они решаются на вычислителе.
Для системы (1) получить аналогичное решение нельзя в силу свойств эллиптических интегралов, как было сказано выше.
Таким образом, в статье показано, что использование геометрии Лобачевского расширяет математические возможности решения геометрических задач на криволинейной поверхности.
Список литературы
1.Даренская Л.В. Векторный метод решения геодезических задач // Известия ВУЗов. Геодезия и фотосъемка. М., — 1980. — № 2. — С. 38—42.
2.Даренская Л.В. К вопросу о решении непрерывных задач в ЭВМ. // Известия ВУЗов. Геодезия и фотосъемка. М., 1989. — № 3. — С. 61—68.
3.Закатов П.С. Курс высшей геодезии. Москва, «Недра», 1976. — 511 с.
4.Морозов В.П. Курс сфероидической геодезии. Москва, «Недра», 1979. — 296 с.
дипломов


Оставить комментарий