УПРУГОПЛАСТИЧЕСКОЕ  СОСТОЯНИЕ  НЕОДНОРОДНОЙ  ТРУБЫ  ИЗ  АНИЗОТРОПНОГО  МАТЕРИАЛА,  НАХОДЯЩЕЙСЯ  ПОД  ДЕЙСТВИЕМ  ВНУТРЕННЕГО  ДАВЛЕНИЯ

Никитин  Андрей  Витальевич

аспирант  кафедры  математического  анализа  Чувашского  государственного  педагогического  университета  им.  И.  Я.  Яковлева,  РФ,  г.  Чебоксары

E-mail: 

ELASTOPLASTIC  STATE  OF  A  NONHOMOGENEOUS  PIPE  MADE  OF  ANISOTROPIC  MATERIAL  UNDER  INFLUENCE  OF  INNER  PRESSURE

Andrey  Nikitin

post  graduate  student  of  the  chair  of  Mathematical  Analysis,  Chuvash  State  Pedagogical  University  named  after  I.Y.  Yakovlev,  Russia  Cheboksary

АННОТАЦИЯ

В  данной  работе  рассматривается  упругопластическое  состояние  трубы  из  анизотропного  материала,  находящейся  под  действием  внутреннего  давления.  Материал  предполагается  неоднородным.  Решение  производится  методом  малого  параметра.  Определены  напряжённое  состояние  и  граница  раздела  упругой  и  пластической  областей  в  нулевом  и  первом  приближении.

ABSTRACT

The  paper  examines  an  elastoplastic  state  of  a  pipe  made  of  anisotropic  material,  which  is  under  the  influence  of  inner  pressure.  Material  is  supposed  to  be  nonhomogeneous.  The  solution  has  been  made  by  small  parameter  method.  State  of  stress  and  interface  of  elastic  and  plastic  domains  at  null  and  initial  approximation  have  been  defined. 

Ключевые  слова:  труба;  неоднородность;  анизотропия.

Keywords:  pipe;  nonhomogeneity;  anisotropy. 

В  данной  работе  рассматривается  развитие  идей  [3,  4,  5,  6,  7],  а  именно  наложение  трансляционной  анизотропии  на  неоднородность  материала. 

Рисунок  1.  Толстостенная  труба  радиусов  ;

Рассмотрим  толстостенную  трубу  радиусов  ,    (рис.  1).  Условие  пластичности  примем  в  виде  [1]:

  ,  (1)

где    компоненты  напряжения  в  декартовой  системе  координат.

Положим:

    (2)

где:  —  малый  безразмерный  параметр.

Используя  связь  между  компонентами  напряжений  в  декартовой  системе  координат    и  компонентами  напряжений  в  полярной  системе  координат  ,  из  (1)  и  (2)  получим:

  (3)

где 

Предположим 

  (4)

Тогда    где    

Положим,  что  искомое  решение  зависит  от  малого  параметра  ,  решение  будем  искать  в  виде

,      (5)

где:    —  радиус  пластической  зоны.        

В  нулевом  приближении  напряжённое  состояние  в  упругой  и  пластической  областях  имеет  вид:

.  (6)

.  (7)

Радиус  упругопластической  зоны  в  нулевом  приближении  определяется  соотношениями:

.

В  первом  приближении  получим:

  (8)

Удовлетворим  уравнения  равновесия,  полагая:

.    (9)

Из  (8),  (9)  имеет  место:

  (10)

В  первом  приближении  граничные  условия  согласно  [2]  имеют  вид:

  (11)

Решение  в  пластической  зоне  будет  определяться  из  (8),  (9),  (10),(11):

             (12)

Напряжения  в  упругой  области  определим  согласно  [2]:

    (13)

Из  (12),(13)  получим  границу  упругопластической  области  в  первом  приближении:

  (14)

Таким  образом,  напряженное  состояние  в  пластической  (12)  и  упругой  (13)  зонах  полностью  определено.  Изменение  границы  пластической  зоны  определяется  из  соотношений  (14).

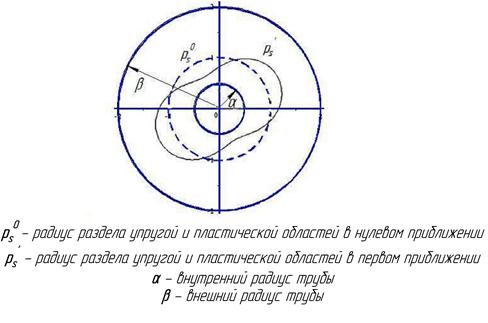
Рисунок  2.  Граница  раздела  упругой  и  пластической  областей  в  нулевом  и  первом  приближении

Граница  раздела  упругой  и  пластической  областей  в  нулевом  и  первом  приближении  представлена  на  (рис.  2).

Список  литературы:

1.Ивлев  Д.Д.  О  соотношениях  теории  трансляционной  идеально-пластической  анизотропии  при  обобщении  условия  пластичности  Мизеса  /  Д.Д.  Ивлев,  Л.А.  Максимова  //  Вестник  Чуваш.  гос.  пед.  ун-та  им.  И.Я.  Яковлева.  Серия:  Механика  предельного  состояния.  —  2010.  —  №  2(8).  —  Ч.  3.  —  С.  583—584. 

2.Ивлев  Д.Д.  Метод  возмущений  в  теории  упругопластического  тела  /  Д.Д.  Ивлев,  Л.В.  Ершов.  М.:  Наука,  1978.  —  208  с.

3.Максимова  Л.А.,  Тихонов  С.В.  Об  упругопластическом  состоянии  неоднородной  трубы,  находящейся  под  действием  внутреннего  давления/  Л.А.  Максимова,  С.  В.  Тихонов//  Вестник  ЧГПУ  им.  И.  Я.  Яковлева.  Серия:  Механика  предельного  состояния.  —  2007.  —  №  2.  —  С.  91—95  . 

4.Митрофанова  Т.В.  Об  условиях  трансляционной  анизотропии  идеальнопластических  тел  при  кручении  /  Т.В.  Митрофанова  //  Вестник  Чувашского  государственного  педагогического  университета  им.  И.Я.  Яковлева.  Серия:  Механика  предельного  состояния.  —  2010.  —  №  2  (8).  —  Ч.  3.  —  С.  596—600. 

5.Тихонов  С.В.  Упругопластическое  состояние  неоднородных  тел,  ослабленных  отверстиями  :  автореф.  дис.  …  канд.  физ.-мат.  наук  :  01.02.04  /  С.В.  Тихонов.  Чебоксары,  2007.  —  75  с.

6.Фоминых  С.О.  Упругоидеальнопластическое  состояние  анизотропной  трубы  /  Фоминых  С.О.  //  Вестник  ЧГПУ  им.  И.Я.  Яковлева.  Серия:  Механика  предельного  состояния.  —  2010.  —  №  2(8).  —  Ч.  3.  —  С.  623—627. 

7.Фоминых  С.О.  Упругопластическое  состояние  толстостенной  трубы  при  взаимодействии  различных  видов  пластической  анизотропии  /  Фоминых  С.О.  //  Вестник  ЧГПУ  им.  И.Я.  Яковлева.  Серия:  Механика  предельного  состояния.  —  2011.  —  №  1(9).  —  С.  201—216  .