ВОЗМОЖНОСТЬ  ПОНИЖЕНИЯ  ТЕМПЕРАТУРЫ  ПРИ  ФОРМИРОВАНИИ  ПЛАЗМЕННОГО  ВИХРЯ  ЭЛЕКТРИЧЕСКИМ  РАЗРЯДОМ

Трощиев  Юрий  Витальевич

канд.  физ.-мат.  наук,  ст.  научный  сотрудник  факультета  ВМК  МГУ  имени  М.В.  Ломоносова,  РФ,  г.  Москва

E-mail: 

POSSIBILITY  OF  TEMPERATURE  DECREASE  UPON  FORMING  OF  PLASMA  VORTEX  BY  ELECTRIC  DISCHARGE

Yuri  Troshchiev

Ph.D.,  senior  Researcher  of  CMC  Department  of  M.V.  Lomonosov   MSU,  Russia  Moscow

АННОТАЦИЯ

В  работе  моделируется  процесс  образования  плазменного  вихря  в  результате  электрического  разряда.  Показывается  численно  и  аналитически,  что  температура  внутри  разрядной  трубки  может  сильно  понижаться.  Понижение  температуры  происходит  за  счет  потери  внутренней  энергии  газа  при  расширении,  сопровождающемся  совершением  работы.  Это  может  снижать  среднюю  температуру  вихря.  Частицы  сконденсировавшихся  газов  могут  менять  газодинамические  свойства  вихря.

ABSTRACT

Process  of  plasma  vortex  forming  by  electric  discharge  is  modeled  in  the  paper.  It  is  numerically  and  analytically  shown  that  temperature  in  the  discharge  tube  can  strongly  decrease.  Temperature  decrease  is  caused  by  decrease  of  gas  internal  energy  while  gas  expansion.  It  can  lower  average  vortex  temperature.  Particles  of  condensed  gases  can  change  vortex  gas-dynamical  properties.

Ключевые  слова:   плазменный  вихрь;  математическое  моделирование.

Keywords:  plasma  vortex;  mathematical  modeling.

Уравнения  математической  модели  тороидального  вихря.

В  данной  работе  рассматриваются  эксперименты  по  получению  светящихся  плазмоидов  в  результате  определенным  образом  произведенного  электрического  разряда  [1].  Схема  эксперимента  следующая.  В  середине  чашки  диаметром  около  20  см  находится  трубка  диаметром  3—5  мм.  Из  трубки  импульсом  выталкивается  струя  плазмы,  из  которой  формируется  светящийся  плазмоид.  Предполагается,  что  такие  объекты  являются  лабораторными  аналогами  шаровой  молнии.  Эксперимент  производится  при  атмосферном  давлении  и  комнатной  температуре.  Математическое  моделирование  эксперимента  производится  в  предположении,  что  плазмоид  является  тороидальным  плазменным  вихрем  [2].  В  данной  работе  рассматривается  и  подтверждается  аналитически  возможность  понижения  температуры  при  формировании  плазмоида.  Результат  частично  опубликован  в  работе  [3].  Возможность  понижения  температуры  подтверждается  и  экспериментальными  данными.

Течение  разреженной  плазмы  в  значительной  мере  определяется  движением  воздуха  [2],  поэтому  для  численного  моделирования  процесса  образования  светящегося  плазмоида  воспользуемся  классическими  уравнениями  газовой  динамики  [4].  Зададим  внутри  трубки  временные  источники  вещества  (импульс  увеличения  плотности)  и  энергии  (температуры).  А  всю  систему  поместим  в  некоторый  объем,  достаточно  большой  по  сравнению  с  размерами  трубки  (рис.  1).

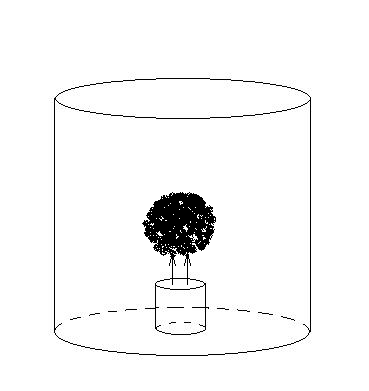
Рисунок  1.  Схема  эксперимента

Математическое  моделирование  рассматриваемых  явлений  удобно  производить  в  условиях  плоско-параллельной  геометрии,  которая  по  сравнению  с  цилиндической  проще  для  расчета  и  выдает  мало  отличающиеся  результаты.  В  этом  случае  координата    является  не  радиусом,  а  одной  из  двух  декартовых  координат  на  евклидовой  плоскости.  Поскольку  вихри  в  такой  геометрии  мы  будем  считать  математической  моделью  тороидальных  вихрей,  то  будем  также  называть  их  тороидальными  и  сохраним  обозначение  .

Будем  рассматривать  уравнения  Навье-Стокса  в  виде:

,  (1а)

Где

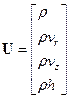,  ,  ,(1б)

,

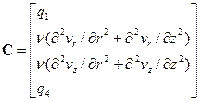.  (1в)

Здесь    —  компоненты  цилиндрических  координат,    —  компоненты  скорости,    —  вязкость,    —  плотность,    —  давление,    —  энтальпия,    —  теплоемкость,    —  температура,    —  молярная  масса  воздуха,    −  универсальная  газовая  постоянная. 

Решения  будем  искать  в  области 

,  .  (2)

На  границах  области  зададим  нулевые  значения  скорости

  (3а)

а  при    условия

,  ,  ,  ,  .  (3б)

На  поверхности  трубки  также  как  и  на  границах  области  зададим  нулевые  значения  скорости

.  (3в)

Отметим,  что  условия  (3в)  выполняются  дважды:  с  одной  и  с  другой  стороны  поверхности  трубки.  Здесь    —  радиус  трубки,    —  высота  трубки.  Давление    и  энтальпия    на  линии  ,    испытывают  разрыв.  Если  толщина  стенок  трубки  ненулевая,  то  условия  (3в)  соответствующим  образом  модифицируются.

Начальные  условия  соответствуют  неподвижному  состоянию  воздуха:

,  ,  ,

,  .  (4)

Решать  уравнения  (1)—(4)  будем  с  помощью  разностных  схем  [5].

Характерные  значения  параметров:  радиус  цилиндра  ~5  –  10  см,  высота  цилиндра  ~10—20  см,  температура  ~,  =  28∙0.785+32∙0.215  г/моль  —  молярная  масса  воздуха,  =101325  Па  —  атмосферное  давление,  радиус  трубки  ~2,5  мм,  высота  трубки    ~  5—10  мм,  время  импульса  ~0,01  с.  Источники    описываются  следующими  формулами:

,    (5а)

Где

,

,  (5б)

.

Некоторые  сведения  о  решениях  таких  систем  уравнений  содержатся  также  в  работе  (6).

Моделирование  плазмоида  при  истечении  газа  из  трубки  и  адекватных  значениях  скорости  и  температуры.

Пусть  высота  трубки  —  5  мм,  радиус  —  2,5  мм.  Толщина  стенок  трубки  в  данном  случае  ненулевая.  Источники  вещества  и  температуры  выберем  следующими:  =5000  кг/м³  с,  =2∙10⁶  кг∙K/м³с,    =0  мм,  =2,5  мм.  =0,01  с,  =  .  Вязкость  будем  вычислять  как  значения  квадратичной  функции,  построенной  методом  наименьших  квадратов  по  точкам  :  (0,171),  (300,297),  (500,362),  (700,417),  (1000,490),  (1200,534).  Такие  значения  вязкости  предоставлены  проф.  В.Л.  Бычковым.  Здесь  температура  измеряется  в  градусах  Цельсия,  а  вязкость  в  10^-7  Н∙с/м².

Максимальная  скорость    при  таких  значениях  параметров  по  окончании  импульса  составляет  ~3  м/с,  а  максимальная  температура    ~1500  .  На  рис.  2а  показано  поле  скоростей  течения  воздуха  после  окончания  импульсов.  Температура  у  дна  трубки  опускается  до  низких  значений  ~100      (рис.  2б).  Соответственно  значения  вязкости  при  <0  экстраполируются  той  же  квадратичной  функцией.  Эту  неточность  можно  допустить,  так  как  рассматриваемая  математическая  модель  не  учитывает  также  и  некоторые  процессы,  происходящие  при  таких  температурах.

(a)                                                      (б)

(в)                                             (г)

Рисунок  2.  (a )  Сформировавшийся  тороидальный  вихрь  по  окончании  действия  источников  вещества  и  температуры  (=0,01  с).  (б)  Зависимость  температуры  от    при  =0  мм  (сплошная  линия)  и  от    при  =5  мм  (пунктирная  линия)  в  момент  времени  =0,005  с.  (в)  Зависимость  температуры  от    при  =0  мм  (сплошная  линия)  и  от    при  =0,25  мм  (пунктирная  линия)  в  момент  времени  =0,005  с.  (г)  Зависимость  отклонения  плотности  от  начального  значения  от  координаты    при  =0  мм  (сплошная  линия)  и  от  координаты    при  =0,25  мм  (пунктирная  линия)  в  момент  времени  =0,005  с

На  рис.  2а  изображена  одна  четверть  расчетной  области:  половина  по  высоте  и  половина  по  ширине.  Расчетная  область  в  рассматриваемом  случае  небольшая.  Это  существенно,  так  как  при  малом  объеме  окружающего  пространства  давление  может  более  заметно  повышаться,  и  может  играть  более  существенную  роль  взаимодействие  со  стенками.  Движением  в  данном  случае  оказалась  захвачена  почти  вся  расчетная  область,  т.  е.  скорость  движения  воздуха  почти  во  всем  объеме  больше  3  см/с.  Внутри  трубки  виден  еще  один  тороидальный  вихрь,  вращающийся  в  противоположную  сторону.

На  рис.  2б  показаны  графики  температуры  при  =0  мм  и  при  =5  мм  в  момент  времени,  соответствующий  максимальным  значениям  источников  тепла  и  вещества.  Максимальное  значение  температуры  порядка  1500  .  Видно  низкое,  порядка  100  ,  значение  температуры  у  дна  трубки,  которое  и  является  основным  предметом  данной  работы.  На  рис.  2в  изображен  тот  же  момент  времени,  что  и  на  рис.  2б,  но  масштаб  по  горизонтальной  оси  больше  и  показано  также  распределение  температуры  в  поперечном  сечении.  Видна  точка  минимума  температуры,  которая,  как  будет  видно  из  дальнейшего,  играет  существенную  роль.  На  рис.  2г  изображено  отклонение  плотности  от  начального  значения  в  тот  же  момент  времени,  что  и  на  рис.  2б,в.  Вдоль  оси    видно  сильное  увеличение  плотности  у  дна  трубки  (до  1,2  атм),  затем  сильное  уменьшение  плотности  у  верхнего  края  трубки  (до  1,015  атм),  а  далее  некоторое  заметное  повышение  плотности  во  всей  остальной  области  (до  1,08  атм).  Выясним  правдоподобность  такого  повышения  плотности  в  остальной  области.  Площадь  сечения  области  равна  0,02×0,02=0,0004  м².  Средняя  скорость  течения  газа  за  время  0,005  с  составляла  примерно  1,5  м/с.  А  ширина  щели  0,0025  м.  Поэтому  за  это  время  через  сечение  трубки  поступил  воздух,  суммарное  сечение  которого  составляет  0,005×0,0025×1,50,00002  м²,  т.  е.  примерно  0,05  от  сечения  области.  Поэтому  повышение  среднего  давления  на  величину  порядка  0.08  от  начального  давления  правдоподобно.  Как  будет  показано  в  дальнейшем  на  эффект  понижения  температуры  такое  повышение  давления  влияет  хотя  и  заметно,  но  не  очень  сильно.

На  рис.  3  показано  поле  температуры  в  момент  окончания  импульсов.

Рисунок  3.  Поле  температуры  в  момент  времени  =0.01  с.

Аналитическое  исследование  достоверности  понижения  температуры.

Оценим  насколько  правдоподобно  понижение  температуры  внутри  трубки.  Для  этого  сначала  рассмотрим  одномерную  задачу.

,  (6а)

Где

,  ,  ,  (6б)

Будем  предполагать,  что  вблизи  стенки  существуют  постоянные  по  времени  источники  вещества  и  температуры:

(7)

У  стенки  зададим  нулевые  значения  скорости:

.  (8)

У  правой  границы  краевые  условия  могут  быть  различными.

Предположим,  что  установился  стационарный  режим:

.  (9)

Тогда  в  пределах  существования  источника,  т.  е.  на  интервале    выполнены  равенства

.  (10а)

.  (10б)

Тогда  в  пределах  существования  источников,  т.е  на  интервале 

,

,  (11)

.

Учитывая  краевое  условие  (8),  получаем

.  (12а)

Так  как  ,  то  температура  в  пределах  существования  источников  тоже  равна  константе

.  (12б)

В  более  сложных  геометриях  могут  существовать  точки  экстремума  энтальпии.  В  таких  точках  энтальпию  можно  вынести  за  знак  дивергенции:

.  (13)

Таким  образом,  стационарное  значение  энтальпии  в  точках  экстремума  равно

,  (14а)

а  температуры

,  (14б)

Математически  величины  (12б)  и  (14б)  могут  быть  как  больше,  так  и  меньше  начального  значения  температуры.  Рассмотрим  эту  возможность  с  точки  зрения  физического  смысла.  Известно,  что  при  адиабатическом  расширении  температура  газа  уменьшается.  Следовательно,  она  может  уменьшаться  и  при  расширении,  не  очень  сильно  отличающемся  от  адиабатического.  В  данном  случае  за  счет  расширения  в  системе  непрерывно  происходит  преодоление  внешнего  давления  для  выталкивания  образовавшегося  газа  за  пределы  источников,  увеличение  скорости  газа  и  преодоление  вязкости.  Т.  е.  можно  гарантировать,  что  по  крайней  мере  в  некоторых  областях  температура  газа  будет  ниже  температуры  источника.  Если  температура  источника  понижается  вместе  с  температурой  газа,  то  будет  происходить  и  дальнейшее  понижение  температуры  газа.

Если  температура  источника  выше  начальной,  то  в  смысле  понижения  температуры  ниже  начальной  вопрос  в  том,  будет  ли  преобладать  нагрев  от  источника  тепла  или  охлаждение  в  результате  расширения.  Заметим  также,  что  речь  идет  об  охлаждении  в  некоторой  области,  так  как  суммарно  газ  нагревается.  Поэтому  противоречия  второму  началу  термодинамики  здесь  нет.  Эти  рассуждения  справедливы  и  в  двумерной  и  в  трехмерной  геометриях.  Более  того,  в  этих  геометриях  неоднородность  реальной  задачи  по  пространству  обеспечивает  отклонение  от  среднего  значения  в  различных  точках  пространства  как  в  положительную,  так  и  в  отрицательную  стороны.  Поэтому  понижение  температуры  в  некоторой  области  пространства  в  таких  геометриях  может  быть  более  существенным,  чем  в  одномерном  случае.  В  примере,  приведенном  на  рис.  2,  точка  минимума  температуры  в  пределах  источников  существует,  но  режим  нестационарный.  На  рис.  2в  видны  точка  минимума  температуры  и  профиль  температуры  по    в  сечении  трубки,  соответствующем  этой  точке  минимума.

Поясним  более  подробно  возможность  более  существенного  понижения  температуры  из-за  неоднородности  задачи  по  пространству.  Пусть  установился  стационарный  режим  истечения  газа  из  трубки.  И  пусть  температура  источника  равна  .  Отметим,  что  в  уравнениях  (1)  задан  не  источник  внутренней  энергии,  а  источник  энтальпии,  поэтому  рассматриваемая  здесь  задача  с  температурой  отличается  от  задачи  для  уравнений  (1).  Если  температура  источника  равна  ,  а  температура  выходящего  из  трубки  газа  равна  ,  то  внутренняя  энергия  газа,  проходящего  через  выходное  отверстие  трубки  за  время    приблизительно  равна

.  (15)

Здесь    —  площадь  сечения  трубки,    —  скорость  истечения  газа,    —  плотность  воздуха  на  выходе  из  трубки.  За  такое  же  время    весь  этот  газ  поступает  из  источника,  поэтому  поступившая  в  систему  внутренняя  энергия  равна

.  (16)

Здесь    —  по-прежнему  плотность  на  выходе  из  трубки,  хотя  изменения  значения  плотности  по  сравнению  с  абсолютным  значением  здесь  очень  маленькие.  Работа,  совершенная  газом  за  это  время  равна

,  (17)

где:    —  давление.  Таким  образом,  в  среднем  выполнено  равенство

.  (18)

Сокращая  на    получаем

.  (19)

Если  подставить  в  это  равенство  значения  величин,  соответствующие  атмосферным  условиям,  то  получается  понижение  температуры,  более  чем  на  100  градусов.  Из  этой  формулы  также  видно,  что  повышение  давления  на  величину  порядка  0,1  от  начального  увеличит  разность  температур    не  очень  значительно.

Основная  часть  работы  совершается  у  дна  трубки,  потому  что  там  давление  оказывает  воздействие  на  весь  газ,  находящийся  в  трубке.  Поэтому  там  понижение  температуры  будет  более  существенным.  Это  можно  выразить  формулой

.  (20)

Здесь  величина    описывает  объем  газа  около  дна  трубки,  а  —  объем  остального  газа  в  трубке.  Время    —  это  время,  которое  понадобилось  бы,  чтобы  газ  находящийся  у  дна  трубки  и  летящий  со  скоростью    прошел  через  сечение  трубки.  Температура    окажется  меньше  температуры  .  И  это  различие  будет  тем  значительнее,  чем  меньшую  относительную  часть  занимает  газ,  совершающий  основную  часть  работы.

В  частности  возможно  более  высокое  значение  температуры  ,  чем  ,  в  результате  совершенной  над  этой  частью  газа  работы.  Источник  вещества  в  рассматриваемой  задаче  очень  мощный:  в  точке  максимальной  интенсивности  источника  за  одну  секунду  плотность  вещества  увеличивается  по  сравнению  с  первоначальной  более,  чем  в  4000  раз.  Поэтому  явления  нагревания  газа  от  сжатия  могут  быть  очень  существенными.

Возможность  понижения  температуры  нетрудно  подтвердить  экспериментально.  Если  выпускать  газ  из  баллона  со  сжиженным  газом,  то  баллон  сильно  охлаждается.  Причем  охлаждается  в  той  части,  где  находится  газообразная,  а  не  жидкая  фаза.  Т.  е.  это  именно  результат  расширения  газа,  а  не  испарения  жидкости.  Можно  также  использовать  аэрозольный  баллончик,  но  эффект  менее  выражен  из-за  тонкой  и  хорошо  проводящей  тепло  оболочки.  Характерное  время  понижения  температуры  оболочки  баллона  в  таких  условиях  минуты  и  десятки  минут.

Оценим,  за  какое  время  будет  происходить  понижение  температуры  в  условиях,  соответствующих  изучаемому  эксперименту.  Для  этого  пренебрежем  воздействием  изменения  температуры  на  стационарность  течения.  Это  можно  сделать  вблизи  стационарных  значений  температуры  вследствие  малых  изменений  плотности,  так  как  газ  в  рассматриваемых  условиях  почти  несжимаем.  Зависимость  плотности  от    и    при  этом  отсутствует.  Поэтому  выполнено  равенство

.  (21)

Рассмотрим  уравнение  для  температуры  (коэффициент  пропорциональности  между  температурой  и  энтальпией  в  данном  случае  постоянен  и  равен  1)

.  (22)

Вблизи  максимумов  и  минимумов  можно  считать  температуру  постоянной.  Учитывая  также  отсутствие  зависимости  плотности  от  времени  получаем  уравнение  для  температуры  в  окрестности  экстремума:

.  (23)

Решением  такого  уравнения  является  функция

.  (24)

Приблизительные  значения  входящих  в  уравнение  величин:  =,  =1,2  кг/м³,  =5000  кг/м³  с,  =2∙10⁶  кг∙K/м³с.  При  отсутствии  источника  энергии  ()  показатель  экспоненты  при  начальной  температуре  отрицателен  порядка  5000.  Время  уменьшения  функции

,    (25)

в  два  раза  равно

.  (26)

Соответственно  время  уменьшения  температуры  в  два  раза  при  показателе  экспоненты    порядка  10^-4с.  При  =2∙10⁶  правая  часть  уравнения  (23)  положительна,  а  при  =10⁶  —  отрицательна  и  стационарное  значение  температуры  равно  240    (меньше  нуля  по  Цельсию).  Первое  из  этих  значений  соответствует  подъему  максимальной  температуры  до  1500  °С,  а  второе  —  до  750  °С.  Оба  значения  являются  физически  осмысленными  и  предполагаемыми  в  рассматриваемом  эксперименте.  И  хотя  рассматривается  расчет,  соответствующий  1500  °С,  но  сделанные  при  аналитической  оценке  погрешности  делают  понижение  температуры  и  в  этом  случае  правдоподобным.  А  показатель  экспоненты  при  этом  может  оказаться  на  порядок  или  два  меньше,  т.  е.  –500  или  –50.  Время  уменьшения  температуры  в  два  раза  будет  соответственно  порядка  10^-3  или  10^-2  с.

Заключение.

В  данной  работе  рассмотрена  начальная  стадия  процесса  формирования  плазменного  сфероида.  Т.  е.  рассматриваются  результаты  расчета  во  время  действия  импульсов.  Внутри  трубки  температура  опускается  до  очень  низких  значений.  Это  может  приводить  к  существованию  различных  процессов,  которые  могут  оказывать  воздействие  на  формирование  и  развитие  вихря.  Например,  в  вихре,  возможно,  присутствуют  капли  и  кристаллы  сконденсировавшихся  и  замерзших  газов,  которые  меняют  газодинамические  свойства  вихря  и  увеличивают  его  за  счет  центробежных  сил.

Список  литературы:

1.Егоров  А.И.,  Степанов  С.И.,  Шабанов  Г.Д.  Демонстрация  шаровой  молнии  в  лаборатории.  УФН,  —  2004,  174,  —  №  1,  —  с.  107—109.

2.Кузьмин  Р.Н.,  Савенкова  Н.П.,  Бычков  В.Л.,  Складчиков  С.А.,  Трощиев  Ю.В.  Математическое  моделирование  тороидальных,  вихревых  и  сферических  долгоживущих  образований.  Материалы  17-й  российской  конференции  по  холодной  трансмутации  ядер  химических  элементов  и  шаровой  молнии.  Дагомыс,  26  сентября  —  3  октября  2010  г.,  —  с.  154—165.

3.Трощиев  Ю.В.  О  возможности  понижения  температуры  в  гатчинском  разряде.  М.,  МАКС  Пресс,  2012,  —  4  стр.

4.Милн-Томпсон  Л.М.  Теоретическая  гидродинамика.  М.,  1964,  —  655  с.

5.Самарский  А.А.  Введение  в  теорию  разностных  схем.  М:  Наука,  1971,  —  552  с.

6.Юсупалиев  У.,  Савенкова  Н.П.,  Трощиев  Ю.В.,  Шутеев  С.А.,  Складчиков  С.А.,  Винке  Е.Э.,  Гусейн-заде  Н.Э.  Вихревые  кольца  и  плазменные  тороидальные  вихри  в  однородных  неограниченных  средах.  II.  Исследование  процесса  образования  вихря.  —  Краткие  сообщения  по  физике  ФИАН,  №  9,  2011  г.,  —  с.  46—58.  (U.  Yusupaliev,  N.P.  Savenkova,  Yu.V.  Troshchiev,  S.A.  Shuteev,  S.A.  Skladchikov,  E.E.  Vinke  and  N.G.  Gusein-zade.  Vortex  rings  and  plasma  toroidal  vortices  in  homogeneous  unbounded  media.  II.  The  study  of  vortex  formation  process.  Bulletin  of  the  Lebedev  Physics  Institute,  38,  2011,  —  pp.  275—282).