ДИНАМИКА  ЧИСЛЕННОСТЕЙ  ТРЕХ  ПОПУЛЯЦИЙ  ТИПА  «ХИЩНИК-ДВЕ  ЖЕРТВЫ»  С  НЕПЕРЕКРЫВАЮЩИМИСЯ  ПОКОЛЕНИЯМИ

Аматов  Михаил  Александрович

канд.  физ.-мат.  наук,  доцент  кафедры  математического  анализа  Белгородского  государственного  национального  исследовательского  университета,  РФ,  г.  Белгород

E -mail:  amatovm@bsu.edu.ru

Аматова  Галина  Михайловна

канд.  физ.-мат.  наук,  доцент  кафедры  педагогики  и  методики  начального  образования  Белгородского  государственного  национального  исследовательского  университета,  РФ,  г.  Белгород.

E-mail: 

POPULATION  DYNAMICS  IN  THE  ‘PREDATOR-TWO  PREYS’  MODEL  WITH  NON-OVERLAPPING  GENERATIONS

Mikhail  Alexandrovitch  Amatov

candidate  of  physical  and  mathematical  sciences,  docent,  department  of  mathematical  analysis,  Belgorod  State  National  Research  University,  Russia  Belgorod

Galina  Mikhaylovna  Amatova

candidate  of  physical  and  mathematical  sciences,  docent,  department  of  pedagogic  and  methods  of  elementary  education,  Belgorod  State  National  Research  University,  Russia  Belgorod

АННОТАЦИЯ

В  статье  исследуются  экологические  приложения  уравнений  в  конечных  разностях  с  разрывными  правыми  частями.  С  помощью  авторской  методики  доопределения  уравнений  на  поверхностях  разрыва  и  компьютерного  моделирования  установлено,  что  при  определенных  значениях  параметров  в  системе  «хищник-две  жертвы»  с  неперекрывающимися  поколениями,  существуют  экологически  устойчивые  режимы. 

Abstract

The  paper  deals  with  ecological  applications  of  finite-difference  equations  with  discontinuous  right-hand  sides.  An  original  method  of  equations  extensive  definitions  on  the  discontinuity  surface  has  proven  the  existence  of  ecologically  stable  modes  at  certain  parameter  values  in  the  ‘predator-two  preys’  model  with  non-overlapping  generations.

Ключевые  слова:   динамика  численности  популяций;  уравнения  в  конечных  разностях;  особые  точки;  разрывные  правые  части;  скользящие  режимы;  «хищник-две  жертвы».

Keywords:  population  dynamics;  finite-difference  equations;  singular  points;  discontinuous  right-hand  sides;  slide  mode;  “predator-two  preys”.

Разностные  уравнения  для  описания  динамики  численностей  популяций  с  неперекрывающимися  поколениями,  могут  быть  получены  либо  с  помощью  «гипотезы  встреч»,  предложенной  еще  В.  Вольтера  [4,  с.  22],  либо  из  дифференциальных  уравнений  [5,  с.  18].  В  том  и  другом  случаях  система  трех  популяций  «хищник-две  жертвы»  будет  описываться  системой  разностных  уравнений  (1):

                                 (1)

где:    —  положительные  константы, 

  —  численности  жертв  в  момент  времени  , 

  —  их  численности  в  следующий  момент  .  Из  биологических  соображений  следует  считать,  что  . 

Выбрав  в  первом  октанте  ,  произвольную  точку    с  помощью  уравнений  (1)  получим  последовательность  точек  где  .  Соединив  каждые  две  соседние  точки    и    отрезками  прямых,  получим  ломаную  ,  которую  и  будем  называть  траекторией  системы  (1).

Последовательности  вершин    траектории    могут  быть  получены  и  как  итерации  отображения  :

Из  биологического  смысла  ясно,  что  для  всех    должны  выполняться  неравенства  ,  ,  ,  т.е.    .  Если  же    при  каком-либо  значении  ,  то  биологически  это  означает  гибель,  по  крайней  мере,  одной  из  популяций,  а  значит  вырождение  всей  системы.

Легко  проверить,  что    отображает  область  ,  где  ,  во  множество  .  Это  означает,  что  если  при  некотором  ,  ,  то  ,  т.е.  система  вырождается.  Покажем,  что  при  любом  выборе  начальной  точки    траектория    системы  (1),  начинающаяся  в  ,  за  конечное  число  шагов  покинет  область.

Рассмотрим  бесконечную  последовательность  областей    ,  задаваемых  неравенствами:

.

Легко  проверить,  что  ,  .  При  этом  объединение    совпадает  с  областью  .

Из  равенства    следует,  что  для  любой  точки    найдется  номер    такой,  что  .  Но  тогда,  используя  отображение  ,  имеем  ,    ,  т.е.  одна  из  популяций  погибает.

Обозначим  через    область,  задаваемую  неравенствами

и  представляющую  собой  внутренность  прямой  треугольной  призмы. 

Рассуждая  методом  от  противного,  докажем,  что  любая  траектория  ,  начинающаяся  в  точке  ,  за  конечное  число  шагов  выходит  из  области    и  попадает  в  область  .

Действительно,  предположим,  что  траектория    целиком  лежит  в  области  .  Тогда  последовательность    вершин  траектории    будет  иметь,  по  меньшей  мере,  одну  предельную  точку,  лежащую  в  замыкании  .

Из  неравенства    следует,  что  ,  т.е.  последовательность  аппликат    вершин    ломаной    строго  убывает.  Из  убывания    и  свойств  отображения    на  границе  области    легко  устанавливается,  что  последовательность    не  имеет  предельных  точек  в  .

Полученное  противоречие  доказывает,  что  любая  траектория  ,  начинающаяся  в  области  ,  за  конечное  число  шагов  выходит  из  нее  и  попадает  сначала  в  область  ,  а  затем  в  ,  что  и  означает  вырождение  системы  (1).

Однако  в  реально  существующих  экосистемах  типа  «хищник-две  жертвы»  все  три  популяции,  как  известно,  существуют  (при  отсутствии  вмешательства  извне)  тысячелетиями,  и  ни  одна  из  них  не  исчезает  и  не  имеет  неограниченно  растущую  численность  [6].  Это  свидетельствует  о  том,  что,  уравнение  (1),  с  постоянными  коэффициентами  не  вполне  адекватно  отражают  поведение  реальных  экосистем.  Чтобы  иметь  математическую  модель,  более  корректно  описывающую  динамику  численностей  таких  популяций,  следует  полагать,  что  некоторые  из  коэффициентов  системы  (1)  зависят  от  фазовых  переменных.

Зависимость  коэффициентов  системы  (1)  от  фазовых  переменных  может  быть  найдена  экспериментально.  Но  в  таком  случае  каждую  экологическую  систему  придется  исследовать  отдельно,  что  затруднит  выявление  общих  закономерностей.  Избежать  этих  затруднений  позволяет  использование  разностных  уравнений  с  разрывными  правыми  частями.

Заменим  систему  разностных  уравнений  (1)  системой  уравнений  с  кусочно-непрерывными  правыми  частями.  По  аналогии  с  работой  [1]  будем  считать,  что  динамика  численностей  популяций  задается  кусочно-непрерывными  разностными  уравнениями  (2),  (3),  имеющими  разрыв  на  части  плоскости  ,  лежащей  в  .

  (2)

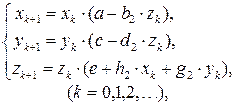    (3)

Определение  решения  системы  (2),  (3)  приведено  в  работах  [2]  и  [3].  Не  ограничивая  общности  рассуждений,  можно  считать,  что  .  Поверхность  разрыва    делит    на  две  части:

  и

.

Динамика  изменения  численностей  популяций  типа  «хищник-две  жертвы»  задается  системой  уравнений  (2)  в  области    и  системой  (3)  в  области  .

Кусочно-непрерывные  разностные  уравнения  (2),  (3)  всегда  имеют  непустую  область  скользящих  движений  .  При  пересечении  траекторией  области  скользящих  движений  дальнейшее  движение  происходит  по  плоскости  .  Мы  не  выписываем  здесь  уравнения  скользящих  движений  и  доказательство  того,  что  их  особая  точка  лежит  в  области  ,  в  виду  их  громоздкости.

С  помощью  программ  для  построения  траекторий  кусочно-непрерывных  разностных  уравнений,  описанных  в  работах  [2]  и  [3],  удалось  доказать,  что  существуют  значения  параметров  системы  (2),  (3)  при  которых  в  ней  имеют  место  устойчивые  в  биологическом  смысле  колебания.

Например,  если  в  системе  (2),  (3)  положить  ,  ,  ,  ,  ,  ,  ,  ,  ,  ,  ,  то  в  ней  возникают  некие  подобия  предельных  циклов  (лежащих  в  области    скользящих  движений  на  плоскости  ),  на  которые  навивают  все  близлежащие  траектории.  На  рис.  1  изображена  траектория,  начинающаяся  в  точке  ,  которая  навивается  на  «цикл».

Рисунок  1.  Предельный  цикл  системы  (2),  (3).  Область  скользящих  движений  затемнена

Нетрудно  найти  значения  параметров,  при  которых  все  траектории  системы  (2),  (3)  будут  покидать  область  .  Не  приводя  здесь  такие  значения,  отметим  лишь  тот  факт,  что  зависимость  коэффициентов  уравнений  (1)  от  фазовых  переменных  оказывается  условием  необходимым,  но  не  является  достаточным  для  устойчивости  экосистемы  «хищник-две  жертвы».

Заключение

Проведенное  исследование  позволяет  сделать  следующие  выводы:

1.  Необходимым  условием  установления  устойчивых  режимов  в  рассматриваемых  экосистемах  является  зависимость  коэффициентов  уравнений  от  фазовых  переменных,  то  есть  от  численностей  этих  популяций. 

2.  В  отличие  от  систем  с  перекрывающими  поколениями  в  уравнениях  динамики  популяций  с  неперекрывающимися  поколениями  существуют  области  ,  при  попадании  в  которые  происходит  вырождение  системы.  Это  свидетельствует  о  большей  уязвимости  таких  систем  по  отношению  к  внешним  воздействиям.  Если  численности  популяций  резко  меняются  и  изображающая  точка  попадает  в  область  ,  то,  по  меньшей  мере,  одна  из  популяций  гибнет.  Такая  ситуация  может  быть  спровоцирована  воздействием  человека. 

3.  Как  следствие  проведенного  исследования,  математически  доказанным  становится  тот  факт,  что  экологически  устойчивой  система  «хищник-две  жертвы»  может  быть  только  в  том  случае,  если  в  периоды  снижения  численности  медленнее  растущей  популяции  хищник  начинает  интенсивней  поедать  ту  популяцию,  которая  растет  быстрее. 

Список  литературы:

1.Аматова  Г.М.  Исследование  модели  взаимодействия  трех  популяций,  связанных  трофическими  отношениями  /  Г.М.  Аматова,  М.A.  Аматов,  И.С.  Кузнецова,  С.А.  Кунгурцев,  Н.А.  Чеканов  //  Экологические  системы  и  приборы.  —  2009.  —  №  7.  —  С.  31—40.

2.Аматов  М.А.  Компьютерное  моделирование  процессов,  описываемых  разрывными  уравнениями  в  конечных  разностях  /  М.A.  Аматов,  Г.М.  Аматова  //  Вопросы  современной  науки  и  практики.  Университет  им.  В.И.  Вернадского.  —  2013.  —  №  2(46).  —  С.  32—38.

3.Аматов  М.А.  Реализация  математической  модели  динамики  систем  кусочно-непрерывных  уравнений  в  конечных  разностях  /  М.A.  Аматов,  Г.М.  Аматова  //  Вестник  Херсонского  национального  технического  университета.  —  2013.  —  №  2(47).  —  С.  29—33.

4.Вольтера  В.  Математическая  теория  борьбы  за  существование  /  В.  Вольтера.  М.:  Наука,  1976.  —  285  с.

5.Пых  Ю.А.  Равновесие  и  устойчивость  в  моделях  популяционной  динамики  /  Ю.А.  Пых.  М.:  Наука,  1983.  —  182  с.

6.Яхонтов  В.В.  Экология  насекомых  /  В.В.  Яхонтов  М.:  Высшая  школа,  1964.  —  459  с.