Статья опубликована в рамках: XVII Международной научно-практической конференции «Естественные и математические науки в современном мире» (Россия, г. Новосибирск, 02 апреля 2014 г.)
Наука: Физика
Секция: Механика деформируемого твердого тела
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
УПРУГОПЛАСТИЧЕСКОЕ СОСТОЯНИЕ НЕЛИНЕЙНО-НЕОДНОРОДНОЙ ТРУБЫ В СЛУЧАЕ ПРИ ТРАНСЛЯЦИОННОЙ АНИЗОТРОПИИ
Статья опубликована в рамках:
Выходные данные сборника:
УПРУГОПЛАСТИЧЕСКОЕ СОСТОЯНИЕ НЕЛИНЕЙНО-НЕОДНОРОДНОЙ ТРУБЫ В СЛУЧАЕ ПРИ ТРАНСЛЯЦИОННОЙ АНИЗОТРОПИИ
Никитин Андрей Витальевич
аспирант кафедры математического анализа Чувашского государственного педагогического университета им. И. Я. Яковлева, РФ, г. Чебоксары
ELASTOPLASTIC STATES OF NONLINEAR INHOMOGENEOUS PIPES IN CASE WHEN TRANSLATIONAL ANISOTROPY
Andrey Nikitin
postgraduate student, Department of Mathematical Analysis, I. Yakovlev Chuvash State Pedagogical University, Russia Cheboksary
АННОТАЦИЯ
В работе исследуется упругопластическое состояние нелинейно-неоднородной трубы при трансляционной анизотропии. Предполагается, что предел текучести постоянен вдоль эллиптических кривых. Труба находится под действием внутреннего давления. Определены напряжённое состояние и граница раздела упругой и пластической областей в нулевом и первом приближении.
ABSTRACT
We study the nonlinear elastic-plastic state inhomogeneous pipe at the translational anisotropy. It is assumed that the yield stress is constant along the elliptic krivyh.Truba is subjected to internal pressure. Defined state of stress and interface elastic and plastic regions in zero and first approximation.
Ключевые слова: труба; упругость; пластичность; анизотропия.
Keywords: pipe; firmness; plasticity; anisotropy.
Условие пластичности для толстостенной трубы радиусов ![]() ,
, ![]() (рис. 1) согласно [1] имеет следующий вид:
(рис. 1) согласно [1] имеет следующий вид:

![]() , (1)
, (1)
где: ![]() компоненты напряжения в декартовой системе координат.
компоненты напряжения в декартовой системе координат.

Рисунок 1. Толстостенная труба радиусов ![]() ,
, ![]()
Предел текучести определим в виде:

![]()
![]()
![]()
![]()
![]() (2)
(2)
где: ![]() — малый безразмерный параметр.
— малый безразмерный параметр.
Перейдем к полярным координатам в формуле (1):
 (3)
(3)
![]()
![]() (4)
(4)
Из (3), (4) условие пластичности в полярных координатах будет иметь вид:
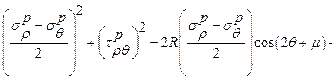
 (5)
(5)
где 
![]()
![]()
Предположим: ![]()
![]()
![]() (6)
(6)
с учетом обозначений имеем:![]()
![]()
Уравнения равновесия в полярной системе координат:
 (7)
(7)
Разложим напряжение ![]() и радиус пластической зоны
и радиус пластической зоны ![]() по малому параметру
по малому параметру ![]() :
:
![]() , (8)
, (8)
В нулевом приближении для осесимметрического состояния трубы
![]() , (9)
, (9)
Из (1), (7), (9) получим:
![]() (10)
(10)
Совместное решение соотношений (7), (9), (10) даёт:
![]()
![]() (11)
(11)
где: С — const.
Предполагается постоянное давление p на внутренней границе трубы а также то, что внешняя граница трубы свободна от усилий:
 , (12)
, (12)
Решая совместно (11), (12) получаем
![]() . (13)
. (13)
В упругой области нулевое приближение имеет вид:
![]()
![]()
![]() (14)
(14)
Условия сопряжения компонент напряжений на упругопластической границе:
![]() (15)
(15)
Из (13), с учетом (12) и (15) получаем
![]() . (16)
. (16)
В нулевом приближении радиус упругопластической зоны определяется соотношением ![]() .
.
Из (1), (2),(4), (8), (10), (11) имеем:
 (17)
(17)
Положим:
 . 18)
. 18)
Из (17), (18) получим:
 (19)
(19)
Условия равновесия (7) удовлетворяются соотношением (18). С учетом (17), (19) значений граничных условий в первом приближении [1]:
 (20)
(20)
находим решение в пластической зоне:

(21)

Тогда на упругопластической границе при ![]() из (21) вытекает:
из (21) вытекает:
 (22)
(22)
где


 (23)
(23)
Для упругой области согласно [1] находим напряжения:




![]()



 (24)
(24)
На основании(13), (14) в первом приближении получим:
 (25)
(25)
Границу упругопластической области в первом приближении найдём из (21), (24), (25):
![]() (26)
(26)
где




Граница раздела упругой и пластической областей в нулевом и первом приближении представлена на рис. 2.

Рисунок 2. Граница раздела упругой и пластической областей в нулевом и первом приближении
Определено напряженное состояние в пластической (21) и упругой (24) зонах. Изменение границы пластической зоны находится из соотношений (26).
Список литературы:
1.Ивлев Д.Д. Метод возмущений в теории упругопластического тела / Д.Д. Ивлев, Л.В. Ершов. М.: Наука, 1978. — 208 с.
2.Ивлев Д.Д. О соотношениях теории трансляционной идеально-пластической анизотропии при обобщении условия пластичности Мизеса / Д.Д. Ивлев, Л.А. Максимова // Вестник Чувашского государственного педагогического университета имени И.Я. Яковлева. Серия: Механика предельного состояния. — 2010. — № 2 (8). — Ч. 3. — С. 583—584.
3.Кузнецов П.Н. Упругопластическое состояние неоднородной плоскости, ослабленной круговым отверстием, подкрепленной включениями, ограниченными эксцентрическими окружностями, при двуосном растяжении / П.Н. Кузнецов // Вестник Чувашского государственного педагогического университета имени И.Я. Яковлева. Серия: Механика предельного состояния. — 2009. — № 1. — С. 134—141.
4.Максимова Л.А. Об упругопластическом состоянии неоднородной трубы, находящейся под действием внутреннего давления / Л.А. Максимова, С.В. Тихонов // Вестник Чувашского государственного педагогического университета имени И.Я. Яковлева. Серия: Механика предельного состояния. — 2007. — № 2. — С. 91—95.
5.Митрофанова Т.В. Об условиях трансляционной анизотропии идеальнопластических тел при кручении / Т.В. Митрофанова // Вестник Чувашского государственного педагогического университета имени И.Я. Яковлева. Серия: Механика предельного состояния. — 2010. — № 2 (8). — Ч. 3. — С. 596—600.
дипломов


Оставить комментарий