Статья опубликована в рамках: XVIII Международной научно-практической конференции «Естественные и математические науки в современном мире» (Россия, г. Новосибирск, 06 мая 2014 г.)
Наука: Информационные технологии
Секция: Управление в социальных и экономических системах
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
ОЦЕНКА ВЛИЯНИЯ КАЧЕСТВЕННЫХ ПОКАЗАТЕЛЕЙ И УЧЕТ СЕЗОННЫХ КОЛЕБАНИЙ В ЭКОНОМЕТРИЧЕСКИХ МОДЕЛЯХ НА МИКРО И МАКРО УРОВНЕ
Нескородева Татьяна Васильевна
канд. техн. наук, доцент Донецкого национального университета, Украина, г. Донецк
Рябченко Алексей Александрович
студент 2 курса Учетно-финансового факультета Донецкого национального университета, Украина, г. Донецк
E-mail:
ASSESSMENT OF QUALITY INDICATORS AND SEASONALLY ADJUSTED ECONOMETRIC MODEL AT THE MICRO AND MACRO LEVELS
Neskorodeva Tatyana
candidate of engineering sciences associate professor of Donetsk National University Donetsk, Ukraine, Donetsk
Ryabchenko Alexey
student of the 2-nd course of the accounting and financial faculty of Donetsk national university, Ukraine, Donetsk
АННОТАЦИЯ
Целью данной работы являлся анализ деятельности экономических субъектов на микро и макро уровне, при котором возникает необходимость оценки влияния качественных показателей и сезонных факторов на результирующий показатель с целью повышения качества принимаемых решений. Для расчета показателей использовался метод наименьших квадратов. Результаты анализа на основании построенных моделей позволяют повысить качество и обоснованность принимаемых решений при управлении анализируемыми показателями.
ABSTRACT
The aim of this work was to analyze the activity of economic agents at the micro and macro level, in which there is the need to assess the impact of quality indicators and seasonal factors on the resultant figure to improve the quality of decisions. For the calculation of the indicators used by the least squares method. Results of the analysis on the basis of the constructed models can improve the quality and validity of decisions in the management of the analyzed indices.
Ключевые слова: индикативные переменные; метод наименьших квадратов; прогнозирование; качественные показатели.
Keywords : indicative variables; least squares method; forecasting; quality indicators.
При анализе деятельности экономических субъектов на микро и макро уровне возникает необходимость оценки влияния качественных показателей и сезонных факторов на результирующий показатель с целью повышения качества принимаемых решений. В настоящее время накоплены большие объемы информации в базах данных, как на предприятиях, так и в официальных органах статистики Украины. Этот факт позволяет эффективно использовать для анализа эконометрические модели с индикативными переменными, оценка параметров которых осуществляется методом наименьших квадратов (МНК) [1]. Для построения МНК модели адекватной эмпирическим данным необходимо выполнение условий Гаусса-Маркова относительно случайной составляющей модели, кроме того, объем выборки по анализируемым показателям должен быть больше числа параметров модели не менее чем в 7 раз. Также для проведения статистических тестов необходимо, чтобы случайный член в модели имел нормальное распределение. В случае если эти условия не выполняются необходимо или откорректировать модель или применить обобщенный МНК. Проиллюстрируем это на примерах (на микро и макро уровне соответственно).
Пример 1 (Построение и анализ эконометрической модели с индикативными переменными на микроуровне). Выбор поставщика техники на основании анализа надежности работы компьютерной техники трех производителей [3].
Компьютерный клуб в течении последних двух лет закупал технику трех производителей ![]() . Менеджер клуба решил проанализировать надежность работы данной техники. Для этого он собрал данные о возрасте техники
. Менеджер клуба решил проанализировать надежность работы данной техники. Для этого он собрал данные о возрасте техники ![]() в месяцах и времени
в месяцах и времени ![]() (в часах) безаварийной работы до последней поломки по 40 единицам техники. Менеджеру необходимо сформулировать приоритеты при закупке компьютерной техники трех производителей, если единственным критерием является время ее безаварийной работы.
(в часах) безаварийной работы до последней поломки по 40 единицам техники. Менеджеру необходимо сформулировать приоритеты при закупке компьютерной техники трех производителей, если единственным критерием является время ее безаварийной работы.
Уравнение выборочной регрессии, зависимости времени ![]() безаварийной работы компьютерной техники от возраста
безаварийной работы компьютерной техники от возраста ![]() и фирмы производителя имеет вид [1, с. 207]:
и фирмы производителя имеет вид [1, с. 207]:
![]() (1)
(1)
где
|
|
если производитель фирма |
|
в противном случае. |
|
|
если производитель фирма |
|
в противном случае. |
с коэффициентом детерминации ![]() . При этом все коэффициенты уравнения и модель (1) являются статистически значимыми при уровне
. При этом все коэффициенты уравнения и модель (1) являются статистически значимыми при уровне ![]() и предпосылки МНК выполняются.
и предпосылки МНК выполняются.
На основании модели (1) можно сделать вывод, что приоритеты при закупке компьютерной техники трех производителей должны быть следующие: в первую очередь следует покупать технику производителя ![]() , во вторую — производителя
, во вторую — производителя ![]() и в последнюю — производителя
и в последнюю — производителя ![]() .
.
Пример 2. (Построение и анализ эконометрической модели с индикативными переменными на макроуровне). Анализ динамики среднемесячной заработной платы в Украине по видам промышленной и экономической деятельности.
Для сравнительного анализа динамики среднемесячной заработной платы по 6-ти основным видам промышленной деятельности (табл. 1) на основании статистических данных по заработной плате в Украине [2] за период 1995—2011 гг. методами корреляционно-регрессионного анализа была построена модель многофакторной регрессии с индикативными переменными.
Таблица 1.
Виды промышленной деятельности
|
№ |
Вид промышленной деятельности |
|
1 |
Добывающая промышленность |
|
2 |
Перерабатывающая промышленность |
|
3 |
Химическое производство |
|
4 |
Металлургическое производство и производство готовых металл. изделий |
|
5 |
Производство машин и оборудования |
|
6 |
Производство и распределение электроэнергии, газа и воды |
Модель динамики заработной платы с учетом вида промышленной деятельности примет вид:
![]() , (2)
, (2)
где: ![]() — номер периода (
— номер периода (![]() для 1995),
для 1995),





Анализируя построенную модель (2) делаем вывод, что ежегодно среднемесячная заработная плата за данный период возрастала в среднем на 185,43 грн по 6-ти основным видам промышленной деятельности. При этом самый низкий уровень заработной платы наблюдался в металлургическом производстве (на 228,18 грн. ниже среднего по промышленности), самый высокий в добывающей промышленности (на 242 грн. выше среднего по промышленности).
Для сравнительного анализа динамики среднемесячной заработной платы по 10-ти основным видам экономической деятельности (табл. 2) на основании статистических данных [2] за период 1995—2011 гг. методами корреляционно-регрессионного анализа была построена модель многофакторной регрессии с индикативными переменными.
Модель динамики заработной платы с учетом вида экономической деятельности примет вид:
 , (3)
, (3)
где: ![]() — номер периода (
— номер периода (![]() для 1995),
для 1995),
Таблица 2.
Виды экономической деятельности
|
№ |
Вид экономической деятельности |
|
1 |
Сельское хозяйство, охота и связанные с ним услуги |
|
2 |
Промышленность |
|
3 |
Строительство |
|
4 |
Торговля; ремонт автомобилей, бытовых изделий и предметов личного употребления |
|
5 |
Деятельность транспорта и связи |
|
6 |
Финансовая деятельность |
|
7 |
Государственное управление |
|
8 |
Образование |
|
9 |
Здравоохранение и предоставление социальной помощи |
|
10 |
Предоставление коммунальных и индивидуальных услуг; деятельность в сфере культуры и спорта |









Анализируя построенную модель, делаем вывод, что ежегодно среднемесячная заработная плата за данный период возрастала в среднем на 158,32 грн по 10-ти основным видам экономической деятельности. При этом самый низкий уровень заработной платы наблюдался в сельском хозяйстве (на 247,84 грн. ниже среднего по экономике), самый высокий в финансовой деятельности (на 1030,27 грн. выше среднего по экономике).
Пример 3. Анализ сезонных колебаний финансовых показателей. Выявление и анализ сезонных колебаний в изменении экономических показателей можно выполнить с помощью эконометрической модели с сезонными переменными. Например, модель спроса на потребительские кредиты или другие финансовые услуги, учитывающая сезонные колебания будет иметь вид:
![]() (4)
(4)
где
|
|
для зимних месяцев, |
|
иначе, |
|
|
для весенних месяцев, |
|
иначе, |
|
|
для летних месяцев, |
|
иначе. |
Модели спроса для различных сезонов будут иметь вид:
|
|
для осенних месяцев; |
|
|
для зимних месяцев; |
|
|
для весенних месяцев; |
|
|
для летних месяцев. |
При этом если в результате проверки значимости коэффициентов будет сделан вывод, что, например коэффициент ![]() статистически незначим, т. е.
статистически незначим, т. е. ![]() то это значит, что между летними и осенними сезонами различие в спросе несущественно. Если
то это значит, что между летними и осенними сезонами различие в спросе несущественно. Если ![]() , то отсутствует различие между спросом на потребительские кредиты зимой, весной и т. д.
, то отсутствует различие между спросом на потребительские кредиты зимой, весной и т. д.
При наличии достаточного объема статистических данных и выполнении предпосылок МНК результаты анализа на основании построенных моделей позволят повысить качество и обоснованность принимаемых решений при управлении анализируемыми показателями.
Список литературы:
1.Елисеева И.И. Эконометрика: учебник М: «Финансы и статистика», 2003. — 344 с.
2.Офіційний сайт Державного комітету статистики України. — [Электронный ресурс] — Режим доступа. — URL: http://ukrstat.gov.ua/
3.Экономико-математические методы и модели: практика применения в курсовых и дипломных работах: учебное пособие / В.В. Христиановский, Т.В. Нескородева, Ю.Н. Полшков; под ред. В.В. Христиановского – Донецк: ДонНУ, 2012. — 325 с. — [Электронный ресурс] — Режим доступа. — URL: http://ec.donnu.edu.ua/sites/default/files/u141/hristianovskiy_v.v._neskorodeva_t.v._polshkov_yu.n._emmim_praktika_primeneniya_v_kurs._i_dipl._rabotah.pdf
дипломов



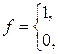
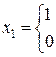


Оставить комментарий