МОДЕЛИРОВАНИЕ  В  ПРЯМОЙ  И  ОБРАТНОЙ  ЗАДАЧАХ  СВОБОДНЫХ  КОЛЕБАНИЙ  МЕХАНИЧЕСКОЙ  СИСТЕМЫ  С  ТРЕМЯ  СТЕПЕНЯМИ  СВОБОДЫ

Сафина  Гульнара  Фриловна

канд.  физ.-мат.  наук,  доцент  Нефтекамского  филиала  БашГУ,  РФ,  г.  Нефтекамск

E-mail: 

MODELLING  FREE  OSCILLATIONS  OF  MECHANICAL  SYSTEM  WITH  THREE  DEGREES  OF  FREEDOM  IN  DIRECT  AND  INVERSE  PROBLEMS

Gulnara  Safina

candidate  of  physical.-  a  mat.  sciences,  associate  professor  of  Neftekamsk  branch  of  BashGU  ,  Russia,  Neftekamsk

АННОТАЦИЯ

В  работе  исследованы  прямая  задача  определения  частот  колебаний  механической  системы  с  тремя  степенями  свободы  и  обратная  задача  диагностирования  массовых  характеристик  системы.  Приведены  алгоритмы  решений  и  их  программные  реализации.

ABSTRACT

The  work  focuses  on  the  direct  problem  of  determining  oscillation  frequencies  of  a  mechanical  system  with  three  degrees  of  freedom  and  the  inverse  problem  of  diagnosing  mass  characteristics  of  the  system.  The  algorithms  of  solutions  and  their  programme  implementations  are  provided. 

Ключевые  слова:  прямая  задача;  частоты  колебаний;  частотное  уравнение;  обратная  задача;  диагностирование  характеристик;  алгоритмы.

Keywords:  direct  task;  frequencies  of  fluctuations;  frequency  equation;  return  task;  diagnosing  of  characteristics;  algorithms.

Прямые  спектральные  задачи  по  свободным  колебаниям  механических  систем  с  конечным  числом  степеней  свободы  рассмотрены  во  многих  классических  трудах  по  теории  колебаний,  например,  в  работах  И.А.  Биргера,  Я.Г.  Пановко,  С.П.  Тимошенко  [2],  [4].

В  отличие  от  последних  работ,  в  представленной  работе  проводится  исследование  в  прямой  задаче  по  свободным  колебаниям  механической  системы  с  тремя  степенями  свободы  с  получением  аналитических  решений  и  программной  реализацией  решения.  Ставится  и  решается  обратная  задача  диагностирования  массовых  характеристик  механической  системы  с  приведением  алгоритма  решения  и  программной  реализации.  Поставленная  обратная  задача  диагностирования  характеристик  механических  систем  решается  с  использованием  только  одного  спектра  частот  их  свободных  колебаний  и  может  быть  обобщена  для  систем  с  большим  числом  степеней  свободы. 

В  качестве  примера  механической  системы  с  тремя  степенями  свободы  рассмотрим  систему  с  тремя  грузами,  соединенными  между  собой  пружинами  [5,  с.  68]  (рисунок  1).

Рисунок  1.  Механическая  система  с  тремя  степенями  свободы

Грузы  массами  ,    и    могут  без  трения  скользить  вдоль  горизонтальной  оси    и  связаны  пружинами,  имеющими  коэффициенты  жесткостей  ,    и  .  За  обобщенные  координаты  примем  перемещения  ,    и    этих  масс  от  положения  статического  равновесия,  соответствующего  отсутствию  напряжений  в  пружинах  [1,  с.  264]. 

Тогда  при  движении  действие  пружин  на  массы  будет  таким,  как  показано  на  (рисунке  1б),  и  уравнения  движения  для  грузов  масс  ,    и    примут  вид:

    (1)

Система  уравнений  (1)  представляет  собой  систему  дифференциальных  уравнений  с  постоянными  коэффициентами.  Так  как  рассматриваем  свободные  колебания  системы,  то  принимаем  частные  решения  уравнений  системы  (1)  в  виде:

    (2)

Здесь    —  частота  свободных  колебаний  механической  системы,  ,  ,  —  амплитуды  колебаний.  Подставляя  функции  (2)  и  их  производные  в  систему  (1),  получим:

Решения  (2)  могут  удовлетворять  уравнениям  (1)  для  всех  значений  времени  ,  если  выполняется  система  уравнений:

    (3)

Решение    уравнений  (3)  определяет  условие  равновесия  механической  системы.  Найдем  теперь  ненулевые  решения,  соответствующие  колебательному  процессу  рассматриваемой  системы  [3,  с.  34]. 

Известно,  что  уравнения  (3)  могут  дать  для  ,    и    отличные  от  нуля  решения  лишь  в  том  случае,  если  равен  нулю  определитель  матрицы  этой  системы:

Откуда 

  (4)

Уравнение  (4)  и  является  частотным  уравнением  свободных  колебаний  рассматриваемой  механической  системы.  Из  этого  уравнения  при  известных  массах  грузов  и  коэффициентов  жесткостей  пружин  можно  определять  частоты  колебаний  механической  системы.

Найдем  аналитическое  решение  уравнения  (4).  Представим  его  в  виде:

Здесь 

Сделав  замену  ,  получим  уравнение  кубическое  уравнение 

С  помощью  подстановки    приведем  последнее  уравнение  к  «неполному»  виду:

    где      (5)

Корни        «неполного»  кубического  уравнения  (5)  равны:

где 

Причем  в  качестве    и    берем  любые  значения  кубичных  корней  из  соответствующих  комплексных  чисел,  удовлетворяющие  соотношению    Если  уравнение  (5)  действительно,  то  (в  тех  случаях,  когда  это  возможно)  следует  брать  действительные  значения  этих  корней.  Если  кубическое  уравнение  (5)  действительно,  то  оно  имеет  или  один  действительный  корень  и  два  сопряженных  комплексных  корня,  или  три  действительных  корня,  по  крайней  мере  два  из  которых  равны,  или  три  различных  действительных  корня  в  зависимости  от  того,  будет  ли    соответственно  положительно,  равно  нулю  или  отрицательно.

Возвращаясь  ко  всем  указанным  выше  заменам,  получим  следующие  аналитические  формулы  для  корней  частотного  уравнения  (4):

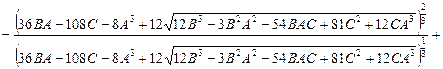
Рассмотрим  прямую  задачу  на  конкретном  примере. 

Пример  1.  Найти  частоты  колебаний  системы  с  тремя  грузами,  для  которой  известны  следующие  физические  параметры:  =2  ,  =3  ,  =1  ,  =4  ,  =2  ,  =1  .

Решение.  Подставим  заданные  значения  масс  грузов  и  коэффициентов  жесткостей  пружин  в  уравнение  (4)  и  найдем  корни  с  помощью  ЭВМ.  Программная  реализация  решения  в  пакете  Maple:

>  print([LABEL  REFERENCE  NOT  SUPPORTED]);  #  input  placeholder

>  print([LABEL  REFERENCE  NOT  SUPPORTED]);  #  input  placeholder

> 

>  print([LABEL  REFERENCE  NOT  SUPPORTED]);  #  input  placeholder

> 

>  print([LABEL  REFERENCE  NOT  SUPPORTED]);  #  input  placeholder

> 

>  print([LABEL  REFERENCE  NOT  SUPPORTED]);  #  input  placeholder

> 

>  print([LABEL  REFERENCE  NOT  SUPPORTED]);  #  input  placeholder

> 

>  print([LABEL  REFERENCE  NOT  SUPPORTED]);  #  input  placeholder

> 

>  print([LABEL  REFERENCE  NOT  SUPPORTED]);  #  input  placeholder

> 

>  print([LABEL  REFERENCE  NOT  SUPPORTED]);  #  input  placeholder

Значит,  частоты  колебаний  следующие:  =0,536,  =1,185,  =1,819.  Заметим,  что  те  же  значения  частот  получаются  по  найденным  выше  аналитическим  формулам. 

Поставим  теперь  к  прямой  спектральной  задаче  обратную  —  задачу  диагностирования  характеристик  механической  системы  по  известным  частотам  его  свободных  колебаний.  К  диагностируемым  характеристикам  отнесем,  например,  коэффициенты  жесткостей  пружин.

При  решении  прямой  задачи  было  получено  частотное  уравнение  (4).  Преобразуем  его  к  виду:

    (6)

в  котором 

  Рассмотрим  метод  решения  задачи.  Если  известны  три  собственные  частоты  ,    и  ,  то  подставляя  их  в  уравнение  (6),  получим  систему  уравнений: 

  (7)

Из  системы  (7)  можно  определить  жесткости  пружин  механической  системы.

Пример  2.  Известны  собственные  частоты  =0,536,  =1,185,  =1,819  колебаний  механической  системы  с  тремя  грузами,  массы  которых  =2,  =3,  =1.  Определить  соответствующие  коэффициенты  жесткостей  ,    и    пружин,  соединяющих  грузы.

Решение.  Подставим  заданные  значения  частот  колебаний  и  масс  грузов  в  систему  (7),  получим:

Из  последней  системы  с  помощью  ЭВМ  найдем  коэффициенты  жесткостей  пружин.  Программная  реализация  решения  в  пакете  Maple:

>  print([LABEL  REFERENCE  NOT  SUPPORTED]);  #  input  placeholder

> 

>  print([LABEL  REFERENCE  NOT  SUPPORTED]);  #  input  placeholder

> 

>  print([LABEL  REFERENCE  NOT  SUPPORTED]);  #  input  placeholder

> 

>  print([LABEL  REFERENCE  NOT  SUPPORTED]);  #  input  placeholder

> 

>  print([LABEL  REFERENCE  NOT  SUPPORTED]);  #  input  placeholder

> 

>  print([LABEL  REFERENCE  NOT  SUPPORTED]);  #  input  placeholder

Таким  образом,  получаем,  что  коэффициенты  жесткостей  пружин,  соответствующие  заданным  частотам  колебаний  механической  системы,  следующие:  ,  ,  .

Заметим,  что  коэффициенты  жесткостей  пружин  определены  верно,  так  как  именно  при  указанных  жесткостях  и  заданных  массах  грузов  при  решении  прямой  задачи  получаются  исходные  частоты  колебаний  механической  системы.

Список  литературы:

1.Блехман  И.И.  Вибрационная  механика.  М.:  Наука,  1994.  —  400  с. 

2.Прочность,  устойчивость,  колебания.  Справочник  в  3-х  т.  /  Под  ред.  И.А.  Биргера  и  Я.Г.  Пановко.  М.:  Машиностроение,  —  1968.  —  Т.  1.  —  831  с.

3.Cафина  Г.Ф.  Акустическое  диагностирование  механических  систем.  Ч.  1.  Уфа:  РИЦ  БашГУ,  2013.  —  109  с.

4.Тимошенко  С.П.  Колебания  в  инженерном  деле.  М.:  Физматгиз,  1959.  —  440  с.

5.Яблонский  А.А.,  Норейко  С.С.  Курс  теории  колебаний.  М.:  Лань,  2003.  —  256  с.