Статья опубликована в рамках: XXIX Международной научно-практической конференции «Естественные и математические науки в современном мире» (Россия, г. Новосибирск, 01 апреля 2015 г.)
Наука: Физика
Секция: Лазерная физика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
УПРАВЛЕНИЕ ИНФОРМАЦИОННОЙ СВЕРТКОЙ КОДИРОВАННЫХ ИМПУЛЬСОВ ПРИ ОБРАБОТКЕ ИЗОБРАЖЕНИЙ
Русанова Инна Александровна
ст. преподаватель кафедры образовательных технологий в физике Казанского федерального университета, РФ, г. Казань
E-mail:
MANAGEMENT INFORMATION CONVOLUTION CODED PULSES
IN IMAGE PROCESSING
Inna Rusanova
teacher the department of educational technology in physics of Kazan federal university, Russia, Kazan
АННОТАЦИЯ
Рассмотрена операция свертки двухимпульсного возбуждения среды с фазовой памятью кодированными импульсами, позволяющими управлять распределением q-битов в пределах неоднородно уширенной линии резонансного перехода, разрабатывать логические элементы и создавать эффективные алгоритмы кодирования информации.
ABSTRACT
The operation of the convolution of the two-pulse excitation of the medium with a phase memory by the coded pulses, allowing to operate the distribution of qubits within the inhomogeneous broadened line of a resonant transition, to develop the logic elements leading and to create effective information coding algorithms.
Ключевые слова: фотонное эхо; оптический эхо-процессор; эхо-голография; квантовая информация; кубит; оптическая обработка информации; обработка изображения; логические элементы.
Keywords: photon echo; optical an echo-processor; echo-holography; quantum information; qubit; optical processing information; processing of images; logic gate.
Введение
Разработка оптических эхо-процессоров позволит осуществить эффективные способы записи и воспроизведения информации. При их создании представляет интерес эхо-голографическая обработка информации. Основными достоинствами оптических запоминающих устройств на основе фотонного эха являются: высокая плотность записи информации; возможность многократного использования резонансной среды для записи; быстродействие и быстрый прямой доступ к ячейкам памяти; возможность записи и считывания информации в реальном масштабе времени [2; 4—6].
Возможности квантовых систем передачи и преобразования информации зависят от сверхплотного кодирования квантовой информации и квантовых алгоритмов, позволяющих более эффективно решать какие-либо задачи. Физическими системами, реализующими q-биты, могут быть любые объекты, имеющие два квантовых состояния: поляризационные состояния фотонов, спиновые состояния ядер и др. Актуальной проблемой на сегодняшний день является организация управления отдельными q-битами и взаимодействия между ними, обеспечивая при этом достаточно большое время декогеренции [3]. В связи с этим интерес представляет исследование оптимизации процессов записи и преобразования информации в оптических эхо-процессорах для разработки логических элементов квантовых компьютеров. Носителем этой информации являются переходные динамические решетки населенностей и поляризаций резонансной среды, которые можно представить как пространственно-частотное распределение q-битов в пределах неоднородноуширенной линии резонансного перехода. В работе использован ранее развитый теоретико-информационный метод исследования квантовых информационных процессов в резонансных средах с фазовой памятью на основе идей Шеннона и алгоритмической теории информации Колмогорова [1; 7—9].
Обработка и преобразование квантовой информации
Информация, полученная и обработанная в квантовых системах, в значительной степени отличается от классической информации. Количество передаваемой классической информации можно увеличить за счет квантового канала связи, безошибочно передающего любое квантовое состояние [3].
Рассмотрим схему записи и воспроизведения явления первичного фотонного эха (ПФЭ), заключающегося в генерируемом эхо-сигнале двухуровневой резонансной средой с фазовой памятью после двухимпульсного воздействия (Рис. 1). Формирование отклика фотонного эха происходит в два основных этапа: расфазирование осциллирующих дипольных моментов оптических центров и их последующее сфазирование, приводящее к возникновению макроскопической поляризации среды, наблюдаемой в виде когерентного отклика.
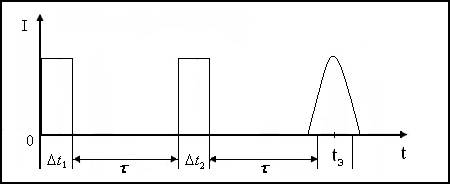
Рисунок 1. Генерирование эхо-сигнала двухуровневой резонансной средой с фазовой памятью после двухимпульсного воздействия в явлении первичного фотонного эха
Кодируемая информация может быть внесена как во временную форму, поляризацию возбуждающего импульса, так и в волновой фронт. В данной работе информация задается на транспаранте с различной кодировкой. Рассмотрим оптические переходные процессы на временах, близких к времени необратимой релаксации среды, при условии относительно большого неоднородного уширения оптических переходов ![]() , позволяющего реализовывать высокую скорость записи и считывания информации (
, позволяющего реализовывать высокую скорость записи и считывания информации (![]() ,
, ![]() ) [2; 7; 8]. Исследуем преобразование количества классической информации, заложенной в кодовый объектный лазерный импульс при его воздействии на систему двухуровневых атомов. Уравнение для одночастичной матрицы плотности запишем в виде
) [2; 7; 8]. Исследуем преобразование количества классической информации, заложенной в кодовый объектный лазерный импульс при его воздействии на систему двухуровневых атомов. Уравнение для одночастичной матрицы плотности запишем в виде
![]() , (1)
, (1)
где ![]() ,
, ![]() и
и ![]() — гамильтонианы атома и среды,
— гамильтонианы атома и среды,
![]() — оператор их взаимодействия,
— оператор их взаимодействия,
![]() — оператор взаимодействия атома с полем излучения. Полагая, что до воздействия объектного импульса атом находился в основном состоянии, для матричных элементов матрицы плотности получим
— оператор взаимодействия атома с полем излучения. Полагая, что до воздействия объектного импульса атом находился в основном состоянии, для матричных элементов матрицы плотности получим
 (4)
(4)
где ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() . (2)
. (2)
После подачи возбуждающего импульса ![]() :
:
![]() , (3)
, (3)
![]() . (4)
. (4)
Информация, заложенная в некоторой структуре, становится потенциальной (структурной). В резонансной среде носителем потенциальной информации являются переходные динамические решетки, описываемые матрицей плотности ![]() , а именно амплитудно-фазовая структура матрицы плотности содержит в себе структурную информацию. Используя ранее развитый теоретико-информационный метод исследования квантовых информационных процессов в резонансных средах и решения для матрицы плотности, при взаимодействии атома с отдельной Фурье — компонентой поля импульса с последующим усреднением по всем частотам, определим количество структурной информации
, а именно амплитудно-фазовая структура матрицы плотности содержит в себе структурную информацию. Используя ранее развитый теоретико-информационный метод исследования квантовых информационных процессов в резонансных средах и решения для матрицы плотности, при взаимодействии атома с отдельной Фурье — компонентой поля импульса с последующим усреднением по всем частотам, определим количество структурной информации ![]() , приходящуюся на отдельную изохромату неоднородно уширенной линии резонансного перехода системы двухуровневых атомов как [7; 8]:
, приходящуюся на отдельную изохромату неоднородно уширенной линии резонансного перехода системы двухуровневых атомов как [7; 8]:
 (5)
(5)
где: ![]() — функция распределения по частотам Фурье — спектра объектного импульса, нормированная на импульс единичной площади,
— функция распределения по частотам Фурье — спектра объектного импульса, нормированная на импульс единичной площади,
![]() — функция распределения по частотам неоднородноуширенной линии резонансного перехода,
— функция распределения по частотам неоднородноуширенной линии резонансного перехода,
 - сумма матричных элементов
- сумма матричных элементов ![]() , при
, при ![]() — эрмитов оператор, с матричными элементами
— эрмитов оператор, с матричными элементами ![]() .
.
В случае реализации операции свертки двухимпульсного возбуждения среды с фазовой памятью, интерес представляет эффективность обработки и преобразования информации в квантовую информацию, в момент времени после подачи второго возбуждающего кодированного импульса (Рис. 2) от площадей возбуждающих импульсов.

Рисунок 2. Зависимость информационной свертки от площадей первого объектного ![]() и второго референтного
и второго референтного ![]() возбуждающих импульсов, с заданной кодировкой транспарантов.
возбуждающих импульсов, с заданной кодировкой транспарантов.
При воздействии второго кодированного импульса, резонансная система переходит в суперпозиционное состояние и наблюдается восстановление когерентности в системе. Путем подбора алгоритма кодирования информации (изображения транспаранта), закладываемой в волновой фронт лазерных импульсов, при двухимпульсном воздействии возможно управление информационной сверткой, что приводит к увеличению квантовой информации среды, уменьшению влияния шумов в квантовом канале связи и построению квантовых алгоритмов при выполнении логических элементов в эхо-процессорах.
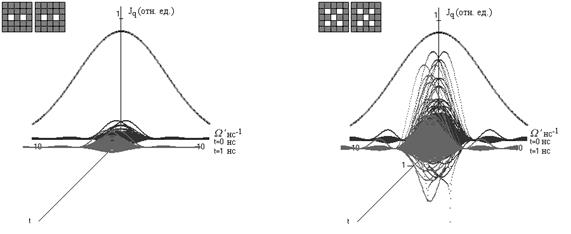
Рисунок 3. Временная эволюция распределения квантовых битов ![]() информационной свертки в пределах неоднородноуширенной линии (
информационной свертки в пределах неоднородноуширенной линии (![]() — момент времени после воздействия второго лазерного импульса с заданной кодировкой транспаранта)
— момент времени после воздействия второго лазерного импульса с заданной кодировкой транспаранта)
На эффективность распределения квантовых битов информационной свертки кодированных импульсов в пределах неоднородного уширения (Рис. 3) оказывает влияние время поперечной обратимой релаксации ![]() , что связано с восстановлением когерентности в системе. Путем подбора алгоритма кодирования информации (изображения), закладываемой в волновой фронт лазерных импульсов, при двухимпульсном воздействии возможно управление информационной сверткой, что приводит к увеличению квантовой информации среды, уменьшению влияния шумов в квантовом канале связи и построению квантовых алгоритмов при выполнении логических элементов в эхо-процессорах [8].
, что связано с восстановлением когерентности в системе. Путем подбора алгоритма кодирования информации (изображения), закладываемой в волновой фронт лазерных импульсов, при двухимпульсном воздействии возможно управление информационной сверткой, что приводит к увеличению квантовой информации среды, уменьшению влияния шумов в квантовом канале связи и построению квантовых алгоритмов при выполнении логических элементов в эхо-процессорах [8].
Список литературы:
1.Колмогоров А.Н. Теория информации и теория алгоритмов. М.: Наука, 1987.
2.Нефедьев Л.А., Самарцев В.В. // ЖПС. — 1987. — № 47 (4). — p. 640.
3.Холево А.С. // УМН. — 1998. — № 53 (6). — p. 193.
4.Kroll S., Tidlund P. // Appl. Optics. — 1993. — v. 32. — p. 7233.
5.Mitsunaga M., Yano R., Uesugi N. // Opt. Lett. — 1991. — № 16. — c. 1890.
6.Mossberg T.W. // Opt. Lett. — 1992. — № 17. — p. 535.
7.Nefed’ev L.A., Rusanova I.А. // Opt. Spektrosk. — 2001. — № 90. — p. 1000.
8.Rusanova I.А. // Quantum electronics. — 2013. — № 43 (7). — p. 651.
9.Shannon C.E. Works on Theory of Information and Cybernetics (Collected Works) Moscow, Inostrannaya Literatura, 1963.
дипломов


Оставить комментарий