Статья опубликована в рамках: XXV Международной научно-практической конференции «Естественные и математические науки в современном мире» (Россия, г. Новосибирск, 03 декабря 2014 г.)
Наука: Физика
Секция: Динамика, прочность машин, приборов и аппаратуры
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
ОПРЕДЕЛЕНИЕ КИНЕТИЧЕСКОЙ ЭНЕРГИИ ВИБРАЦИОННОЙ МАШИНЫ С ДВУМЯ УПРАВЛЯЕМЫМИ ТРЕХДЕБАЛАНСНЫМИ ВИБРОВОЗБУДИТЕЛЯМИ
Черевко Александр Николаевич
канд. техн. наук, зав. кафедрой теоретической механики, доцент Полтавского национального технического университета, Украина, г. Полтава
E-mail:
DETERMINATION OF THE KINETIC ENERGY OF VIBRATING MACHINES WITH TWO CONTROL THREE UNBALANCES EXITERS
Alexandr Cherevko
candidate of Science, Head of Theoretical Mechanics department, assistant professor of Poltava National Technical University, Ukraine, Poltava
АННОТАЦИЯ
Управляемые дебалансные вибровозбудители — основа технологических машин будущего. Генератор колебаний позволяет получать разнообразные нестационарные вибрационные поля переменной структуры. Рассматриваются вопросы, связанные с построением математической модели вибрационной машины с двумя трехдебалансными вибровозбудителями. Для ее составления используются уравнения Лагранжа второго рода. В результате проведенных исследований была определена кинетическая энергия дебалансных валов и неподвижных дебалансов.
ABSTRACT
Controlled unbalance vibration exciters — the basis of machinery technology of the future. The oscillator produces a variety of non-stationary vibrational fields of variable structure. Problems associated with the construction of a mathematical model of the vibrating machine with two three unbalances exciters. For it is made using the Lagrange equations of the second kind. As a result of the research was to determine the kinetic energy of the unbalanced shafts and fixed eccentric weight.
Ключевые слова: дебаланс; вибровозбудитель; математическая модель; кинетическая энергия.
Keywords: eccentric weight; vibration exciter; mathematical model; the kinetic energy.
Моделирование вибрационной машины с управляемыми винтовыми колебаниями рабочего органа представляет собой довольно сложную задачу, связанную с необходимостью описывать свободные движения механической системы.
Свободное движение твердого тела определяется шестью обобщенными координатами, в качестве которых выступают декартовые координаты центра масс тела и углы Эйлера.
Использование при построении математической модели углов Эйлера не совсем удобно [1]. В исследованиях будет использоваться подвижная система, названная проф. Сердюком Л.И. вибрационной [2].
Направим оси координат следующим образом: ось ![]() параллельно дебалансным валам через центр масс подвижного корпуса, ось
параллельно дебалансным валам через центр масс подвижного корпуса, ось ![]() — перпендикулярно к ней вверх, а ось
— перпендикулярно к ней вверх, а ось ![]() — горизонтально. Эти оси совпадают с главными центральными осями подвижного корпуса (рис. 1) машины.
— горизонтально. Эти оси совпадают с главными центральными осями подвижного корпуса (рис. 1) машины.

Рисунок 1. Расчетная схема блока вибровозбудителей
Неподвижные дебалансы 2 и 5 размещены в плоскости ![]() . Подвеска подвижного корпуса выполняется на уровни нижней грани. Подвижные дебалансы перемещаются вдоль дебалансных валов в противоположные стороны (1,3) и (4,6) и поворачиваются от уравновешенного состояния на угол
. Подвеска подвижного корпуса выполняется на уровни нижней грани. Подвижные дебалансы перемещаются вдоль дебалансных валов в противоположные стороны (1,3) и (4,6) и поворачиваются от уравновешенного состояния на угол ![]() по часовой стрелке (1, 4, 6) и против — (3), если смотреть навстречу оси
по часовой стрелке (1, 4, 6) и против — (3), если смотреть навстречу оси ![]() .
.
Используем такие обобщенные координаты:
![]() ,
, ![]() ,
, ![]() — декартовые координаты, которые определяют перемещение центра масс подвижного корпуса машины вдоль соответствующих координатных осей;
— декартовые координаты, которые определяют перемещение центра масс подвижного корпуса машины вдоль соответствующих координатных осей;
![]() — угол, который определяет поворот подвижного корпуса в горизонтальной плоскости вокруг оси
— угол, который определяет поворот подвижного корпуса в горизонтальной плоскости вокруг оси ![]() ;
;
![]() — угол, который определяет поворот подвижного корпуса в вертикальной профильной плоскости вокруг оси
— угол, который определяет поворот подвижного корпуса в вертикальной профильной плоскости вокруг оси ![]() ;
;
![]() — угол, который определяет поворот подвижного корпуса в вертикальной фронтальной плоскости вокруг оси
— угол, который определяет поворот подвижного корпуса в вертикальной фронтальной плоскости вокруг оси ![]() ;
;
![]() — угол, который определяет поворот дебалансного вала относительно собственной оси;
— угол, который определяет поворот дебалансного вала относительно собственной оси;
![]() ,
, ![]() ,
, ![]() — декартовые координаты, которые определяют перемещение центра масс обрабатываемой среды, вдоль соответствующих координатных осей;
— декартовые координаты, которые определяют перемещение центра масс обрабатываемой среды, вдоль соответствующих координатных осей;
![]() ;
; ![]() ;
; ![]() — декартовые координаты, которые определяют перемещение центра масс обрабатываемой среды.
— декартовые координаты, которые определяют перемещение центра масс обрабатываемой среды.
В процессе моделирования вибрационной машины с учетом влияния обрабатываемой среды на движение рабочего органа ограничимся исследованием движения центра масс загрузки согласно теоремы о движении центра масс механической системы [3]. Модель среды в форме представлена в виде одной массы (массы системы), сосредоточенной в центре масс загрузки. С формой она взаимодействует по трем взаимно перпендикулярным направлениям соответствующими связями, которые моделируют жесткость, вязкость и пластичность среды. Основной особенностью такой модели есть то, что она позволяет учитывать изменение реологических свойств среды во время виброобработки.
Для составления математической модели сложной механической системы воспользуемся последовательностью действий, которая определяется уравнениями Лагранжа второго рода
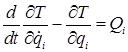
где: ![]() — кинетическая энергия системы;
— кинетическая энергия системы;
![]() — обобщенная координата системы;
— обобщенная координата системы;
![]() — обобщенная скорость системы;
— обобщенная скорость системы;
![]() — обобщенная сила системы.
— обобщенная сила системы.
Определим кинетическую энергию системы как сумму кинетических энергий обрабатываемой среды, корпуса машины, дебалансных валов и дебалансов.
1. Кинетическая энергия корпуса машины.
Корпус машины выполняет свободное движение в пространстве. По теореме Кенига кинетическая энергия твердого тела равна сумме кинетической энергии его поступательного движения вместе с центром масс и кинетической энергии вращательного движения тела вокруг центра масс. Полюс ![]() совпадает с центром масс машины.
совпадает с центром масс машины.
![]() ;
;
где: ![]() — масса корпуса машины;
— масса корпуса машины;
![]() — скорость центра масс.
— скорость центра масс.
![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
;
![]() ;
;

2. Кинетическая энергия дебалансного вала 1.
Дебалансный вал 1 совершает сложное движение. Вращаясь вокруг собственной оси с угловой скоростью ![]() , вместе с корпусом совершает свободное движение:
, вместе с корпусом совершает свободное движение:
![]() .
.
где ![]() — абсолютная скорость центра масс дебалансного вала;
— абсолютная скорость центра масс дебалансного вала;
![]() .
.
 ;
;
где ![]() ,
, ![]() ,
, ![]() — координаты центра масс дебалансного вала;
— координаты центра масс дебалансного вала;
![]() ,
,![]() ,
,![]() .
.
 ;
;
![]() ;
;
 .
.
![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
![]() ;
;  .
.![]() ;
; ![]() .
.
![]() ;
;  .
.
 .
. ![]()

3. Кинетическая энергия дебалансного вала 2.
Дебалансный вал 2 совершает сложное движение. Вращаясь вокруг собственной оси с угловой скоростью ![]() , вместе с корпусом совершает свободное движение:
, вместе с корпусом совершает свободное движение:
![]() .
.
где ![]() — абсолютная скорость центра масс дебалансного вала;
— абсолютная скорость центра масс дебалансного вала;
![]() .
.
 ;
;
где ![]() ,
, ![]() ,
, ![]() — координаты центра масс дебалансного вала;
— координаты центра масс дебалансного вала;
![]() ,
,![]() ,
,![]() ;
;
 ;
;
![]() ;
;
 .
.
![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
![]() ;
;  .
.![]() ;
; ![]() .
.
![]() ;
;  .
.
 .
. ![]()

Определим сумму кинетических энергий двух валов:

Список литературы:
- Сердюк Л.И. Основы теории, расчет и конструирование управляемых вибрационных машин с дебалансными возбудителями: Автореф. дис. докт. техн. наук / Л.И. Сердюк; ХПИ. Харьков, 1991. — 48 с .
- Сердюк Л.І., Черевко О.М., Давиденко Ю.О. Керовані вібраційні машини з дебалансними збуджувачами (теорія, дослідження, конструювання): монографія / Л.І. Сердюк, О.М. Черевко, Ю.О. Давиденко, Полтава: ТОВ “АСМІ”, 2013. — 370 с.
- Яблонский А.А. Курс теоретической механики / Ч. II. Динамика: Учебник для техн. вузов. 6-е изд., испр. М.: Высш. шк., 1984. — 423 с.
дипломов


Оставить комментарий