Статья опубликована в рамках: XXVIII Международной научно-практической конференции «Естественные и математические науки в современном мире» (Россия, г. Новосибирск, 04 марта 2015 г.)
Наука: Физика
Секция: Теплофизика и теоретическая теплотехника
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
ПЕРВОЕ ПРИБЛИЖЕНИЕ ЗАДАЧИ О ПОЛЕ ДАВЛЕНИЯ В НЕОДНОРОДНОЙ ОРТОТРОПНОЙ ПОРИСТОЙ СРЕДЕ
Филиппов Александр Иванович
д-р техн. наук, заведующий кафедрой общей и теоретической физики, профессор Стерлитамакского филиала Башкирского Государственного Университета, РФ, г. Стерлитамак
E -mail: filippovai@rambler.ru
Губайдуллин Марат Радикович
аспирант кафедры общей и теоретической физики Стерлитамакского филиала Башкирского Государственного Университета, РФ, г. Стерлитамак
THE FIRST APPROXIMATION OF THE PROBLEM ABOUT PRESSURE FIELD IN AN ORTHOTROPIC NONHOMOGENEOUS POROUS MEDIUM
Filippov Alexander
dr. Tech. Sciences, Head of the Department of General and Theoretical Physics, Professor, Sterlitamak branch of the Bashkir State University, Russia, Sterlitamak
Gubaidullin Marat
PhD student, Department of General and Theoretical Physics, Sterlitamak branch of the Bashkir State University, Russia, Sterlitamak
АННОТАЦИЯ
Получено аналитическое выражение для первого коэффициента асимптотического разложения задачи о поле давления в неоднородной ортотропной пористой среде, решаемой с помощью модификации «в среднем точного» асимптотического метода. Для построения первого коэффициента использованы добавочные условия, которые найдены на основе требования тривиального решения осредненной задачи для остаточного члена.
ABSTRACT
An analytical expression for the first coefficient of the asymptotic expansion of the problem of the pressure field in an inhomogeneous orthotropic porous medium solved by modifying "the average exact" of the asymptotic method has been received. For the construction of the first coefficient additional conditions were used that were found on the basis of the requirements of the trivial solution of the averaged problem for the remainder term has been received.
Ключевые слова: поле давления; фильтрация; асимптотический метод; неоднородный ортотропный пласт.
Keywords: pressure field; filtering; asymptotic method; inhomogeneous orthotropic layer.
Задача о поле давления в ортотропных пластах имеет практическую значимость для нефтегазодобычи, гидрогеологии, подземного захоронения радиоактивных веществ [5], поскольку по построенным полям давления выявляют застойные зоны, зоны повышенного и пониженного пластового давления, проводят регулирование объемов закачки и отборов жидкости.
Существуют многочисленные решения подобных задач для однородных пористых пластов, однако реальные пласты неоднородны как по толщине, так и по простиранию. Здесь рассматривается задача о полях давления в высокопроницаемом ортотропном слое –h < zd < h, окруженном пористой средой 1, 2 с повышенной вертикальной проницаемостью (рис. 1). Такие пропластки встречаются как в условиях песчаных коллекторов, так и в карбонатных пластах. При закачке и отборе давление в пласте отклоняется от равновесного, величину возмущения в соответствующих пластах обозначим Рd, Р1d, Р2d. Определение этих возмущений является основной задачей фильтрационной гидродинамики. Решить эту задачу позволяет развитая авторами модификация «в среднем точного» асимптотического метода [1, 3—7]
Размерная постановка задачи о полях давления в неоднородных ортотропных пористых средах при линейном течении вдоль оси х содержит уравнения пьезопроводности в соответствующих областях.

Рисунок 1. Геометрия задачи о полях давления в неоднородных ортотропных пористых средах
Для простоты рассмотрим квазистационарный частный случай и пренебрежем горизонтальной проницаемостью настилающего и подстилающего пластов. В этих предположениях постановка задачи примет вид
|
|
(1) |
|
|
(2) |
|
|
(3) |
условия равенства давления
|
|
(4) |
и потоков на границах раздела высокопроницаемого пласта и окружающих проницаемых пород
|
|
(5) |
Рассмотрен режим постоянной депрессии
|
|
(6) |
Предполагается отсутствие возмущений давления на бесконечности
|
|
(7) |
и в начальный момент времени
|
|
(8) |
Задача записана в безразмерном виде с помощью следующих соотношений:
|
|
(9) |
Решение задачи представлено в виде асимптотического ряда по параметру e ![]() . Решение задачи в нулевом приближении представлено в [3] в виде
. Решение задачи в нулевом приближении представлено в [3] в виде
|
|
(10) |
|
|
(11) |
|
|
(12) |
Решение для первого коэффициента разложения осуществлено аналогично [1, 4—5] и имеет вид
|
|
(13) |
|
|
(14) |
|
|
(15) |
где
 ,
,![]() .
.
В справедливости полученных выражений нетрудно убедиться прямой подстановкой выражений в задачи для нулевого и первого коэффициентов, полученных из асимптотического представления исходной задачи.
На рис. 2 представлено сопоставление вертикальных распределений относительного давления в нулевом (пунктирные линии) и первом приближении (сплошные линии) при различных значениях безразмерного времени 1 - t = 1, 2 - Fo = 2. Значения параметров в расчетных формулах приняты равными x=1, k1 = k2 = 1, χ = χ2 =0.2, Χ=0.2.

Рисунок 2. Сопоставление вертикальных распределений относительного давления в нулевом (пунктирные линии) и первом приближении (сплошные линии) при значении безразмерной горизонтальной координаты x =1 и различных величинах безразмерного времени 1 - t = 1, 2 - 2
Список обозначений
h — полутолщины пласта, м; k — проницаемость, м2; t — безразмерное время; Р — безразмерное давление; P01 — характерный перепад давления, Па; Pd – размерное давление, Па; Q – дебит скважины, м3/с; td — время, с; z, x — безразмерные цилиндрические координаты; zd, xd — цилиндрические координаты, м; e — параметр асимптотического разложения; χ — пьезопроводность, м2/с; Индексы нижние: 0 — начальные значения параметров, 1 — номер среды, z, x — направление.
Индексы верхние (в скобках) — порядковый номер коэффициента асимптотического разложения. Обозначения математических символов — общепринятые.
Список литературы:
1.Ахметова О.В., Филиппов А.И., Филиппов И.М. Квазистационарные поля давления при линейной фильтрации в неоднородном анизотропном пласте в асимптотическом приближении. // Механика жидкости и газа. — 2012. — № 3. — С. 89—100.
2.Диткин В.А., Прудников А.П. Справочник по операционному исчислению. М.: Высшая школа, 1965. — 466 с.
3.Филиппов А.И., Ахметова О.В., Ковальский А.А., Губайдуллин М.Р. Поля давления в неоднородных ортотропных пористых средах // Математическое моделирование процессов и систем: Сборник трудов II Всероссийской научно–практической конференции с международным участием (Стерлитамак, 28—29 ноября 2013 г.). Стерлитамакский филиал БашГУ, 2013. — С. 165—169.
4.Филиппов А.И., Ахметова О.В., Филиппов И.М. Фильтрационное поле давления в неоднородном пласте при постоянном отборе // Инженерно-физический журнал. — 2012. — Т. 85, — № 1. — С. 3—17.
5.Филиппов А.И., Ахметова О.В., Заманова Г.Ф. Асимптотические представления упругих волновых полей в проницаемых пластах // Акустический журнал. — 2013. — Т. 59, — № 5, — С. 596—606.
6.Филиппов А.И., Ахметова О.В., Ковальский А.А., Заманова Г.Ф. Фильтрационные волны в слабо анизотропной среде // Вестник Башкирского университета. — 2013. — Т. 18. — № 4. — С. 1004—1005.
7.Чекалюк Э.Б. Основы пьезометрии залежей нефти и газа. Киев: ГИТЛ УССР, 1965. — 286 с.
дипломов


 ,
, 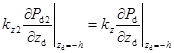 .
. ,
,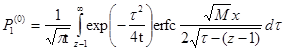 ,
, .
.
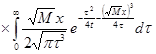 ,
, ,
, ,
,
Оставить комментарий