Статья опубликована в рамках: XXX Международной научно-практической конференции «Естественные и математические науки в современном мире» (Россия, г. Новосибирск, 06 мая 2015 г.)
Наука: Биология
Секция: Экология и природопользование
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
МОДЕЛИРОВАНИЕ ЭКОЛОГИЧЕСКИХ ПРОЦЕССОВ С ИСПОЛЬЗОВАНИЕМ ДИФФЕРЕНЦИАЛЬНЫХ УРАВНЕНИЙ С РАЗРЫВНЫМИ ПРАВЫМИ ЧАСТЯМИ
Аматов Михаил Александрович
канд. физ.-мат. наук, доцент кафедры математики Белгородского государственного национального исследовательского университета, РФ, г. Белгород.
E-mail: amatovma @yandex .ru
Аматова Галина Михайловна
канд. физ.-мат. наук, доцент кафедры педагогики и методики начального образования Белгородского государственного национального исследовательского университета, РФ, г. Белгород.
E-mail:
ENVIRONMENTAL PROCESS MODELING BY MEANS OF DIFFERENTIAL EQUATIONS WITH DISCONTINUOUS RIGHT-HAND SIDES
Mikhail Amatov
candidate of physical and mathematical sciences, docent, department of mathemaca,
Belgorod State National Research University, Russia, Belgorod
Galina Amatova
candidate of physical and mathematical sciences, docent, department of pedagogic and methods of elementary education, Belgorod State National Research University, Russia, Belgorod
АННОТАЦИЯ
В работе моделируется процесс взаимодействия биологических популяций, связанных отношениями продуцент-консумент-хищник с внутривидовой конкуренцией продуцентов. В предлагаемой модели используются дифференциальные уравнения с разрывными правыми частями, специальная методика их «склеивания» и авторская программа интегрирования. Полученная модель позволяет установить зависимость численностей популяций указанного типа от параметров системы.
Abstract
The paper presents an interaction model for biological populations of ‘producer-consumer-predator’ type with intraspecific competition between producers. Presented model makes use of differential equations with discontinuous right-hand sides with a special ‘adhesion’ technique and the authors’ integration program. The model allows to establish a dependency of the populations’ size on system parameters.
Ключевые слова: популяционные волны; продуцент-консумент-хищник; предельные циклы; скользящие режимы.
Keywords: population waves, producer-consumer-predator, limit cycles, slide mode.
Одним из основных направлений развития классической экологии является исследование процессов взаимодействия биологических популяций разных видов. Первые успехи в математическом моделировании этих процессов относятся к первой половине XX века. С тех пор и до настоящего времени это направление активно развивается. Для математического описания динамики численностей различных популяций, чаще всего, используются обыкновенные дифференциальные уравнения или дифференциальные уравнения в частных производных. Авторы данной статьи в течение ряда лет занимаются разработкой моделей взаимодействия трех популяций, используя дифференциальные уравнения с разрывными правыми частями.
Так, в работах [1; 2; 3] определены, строго математически доказаны и биологически обоснованы условия возникновения устойчивых колебаний численностей трех популяций, связанных трофическими отношениями. Найденные описанным образом предельные циклы мало отличаются от эллипса, колебания численностей, как правило, носят почти гармонический характер, а амплитуды их не содержат резких скачков.
Однако не любые три популяции, связанные трофическими отношениями, попадают под ранее исследованные случаи, поскольку амплитуда колебаний численностей некоторых популяций в определенные моменты времени может возрастать или убывать скачкообразно. В природе ярким таким примером являются нашествия саранчи Locusta migratoria или миграция огромных скоплений леммингов Lemmini. «Регулярные циклы численности, такие как у рыси и зайца или леммингов, представляются парадоксальными и загадочными», — замечает Ю. Одум [7, с. 49].
Далее, проанализируем причины, приводящие, по нашему мнению, к резким скачкам численности саранчи. Саранча живет в пустынях и полуаридных зонах, где между различными видами растительности ведется жесточайшая конкурентная борьба за каждый клочок плодородной земли у редких водоемов. Естественными врагами саранчи, являются «некоторые птицы и млекопитающие: розовые скворцы, аисты, чайки, грачи, вороны с ожесточением преследуют саранчу, а галки, жаворонки, кроме того, уничтожают еще яички, выкапывая кубышки из земли» [6].
Иначе говоря, растительная пища саранчи является в экологической системе продуцентом, подверженным внутривидовой конкуренции, а сама саранча — консументом, поедаемым хищниками. Аналогичную зависимость можно установить для леммингов и целого ряда других биологических популяций.
В данной статье рассмотрим моделирование взаимодействия биологических популяций в системе «продуцент-консумен-хищник» при внутривидовой конкуренции продуцента.
Система дифференциальных уравнений, описывающая динамику численностей таких популяций, представлена в монографии А.Д. Базыкина [5] и имеет вид:
 (1)
(1)
Однако вопрос о существовании в ней предельных циклов и других, устойчивых с биологической точки зрения колебательных режимов остался открытым.
Используя методику, описанную авторами в работах [1; 2; 3], заменим систему (1) кусочно-непрерывной системой дифференциальных уравнений, имеющей разрыв на плоскости ![]() , которая в области
, которая в области ![]() задается уравнениями (2), а в области
задается уравнениями (2), а в области ![]() уравнениями (3).
уравнениями (3).
 (2),
(2),
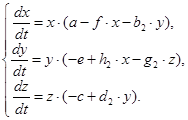 (3).
(3).
В работе [2] (для случая ![]() ) показано, что при
) показано, что при ![]() на плоскости
на плоскости ![]() существует непустая полоса скользящих движений:
существует непустая полоса скользящих движений:  . А поскольку член
. А поскольку член ![]() первого уравнения системы, отвечающий за конкуренцию продуцентов, не входит в последние уравнения системы (2—3), то
первого уравнения системы, отвечающий за конкуренцию продуцентов, не входит в последние уравнения системы (2—3), то ![]() является областью скользящих движений и для нее.
является областью скользящих движений и для нее.
Если в системе (2—3) положить ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , то в ней возникает предельный цикл, начинающийся в точке
, то в ней возникает предельный цикл, начинающийся в точке ![]() и изображенный на рисунке 1.
и изображенный на рисунке 1.

Рисунок. 1. Предельный цикл системы (2—3), область скользящих движений затемнена
Для доказательства существования значений параметров системы (2—3), при которых в ней имеют место устойчивые в биологическом смысле колебания, использовались программы для построения траекторий кусочно-непрерывных систем дифференциальных уравнений, описанные нами в работе [4].
Анализируя поведение траекторий по рис. 1, легко заметить, что промежутки колебаний с малыми амплитудами сменяются промежутками с резко возрастающими амплитудами. Рассмотрим по рис. 2, как происходят колебания численности консумента.

Рисунок 2. Колебания численности консумента
На изображении отчетливо видно, как промежутки (α; β) с малыми колебаниями амплитуды сменяются резкими ее скачками на участках (β; γ).
Здесь важно заметить, что системы уравнений (2—3) никак не учитывают внешние факторы: климат, солнечную активность, случайные флуктуации биотических и абиотических условий среды, морфологические изменения особей и многие другие. А значит, есть все основания утверждать, что скачкообразные изменения амплитуды колебаний консумента являются для рассматриваемой системы внутренним свойством и присущи ей изначально.
А вот как пишет об этом Ю. Одум: «Если будет доказано, что случайные и иные климатические факторы не являются основной причиной резких колебаний численности, то вполне естественно искать причины этих колебаний в самих популяциях («внутренние факторы»). Имеются некоторые данные, свидетельствующие о том, что, по-видимому, существуют какие-то механизмы, которые могут действовать сопряжено с изменениями погоды или других физических факторов» [7, с. 50].
Предлагаемая нами модель позволяет обосновать предположения Ю. Одума о том, что в случае наложения на внутренние скачки амплитуды колебаний численностей популяций каких-либо из указанных или иных внешних факторов происходит резкий взрывообразный рост популяции консумента.
Проведенное исследование позволяет сделать ряд выводов.
1. Необходимым условием установления устойчивых режимов в рассматриваемых экосистемах является зависимость коэффициентов уравнений от фазовых переменных, то есть от численностей этих популяций.
2. Резкие скачки численностей являются свойством, внутренне присущим всем экосистемам, в которых численность продуцента по каким-либо причинам (в частности из за внутривидовой конкуренции) остается на низком уровне.
3. Такие факторы как морфологические изменения, климатические условия, солнечная активность и т.п. могут только усиливать эффект резкого возрастания численности таких популяций.
Список литературы:
1.Аматова Г.М. Исследование модели взаимодействия трех популяций, связанных трофическими отношениями / Г.М. Аматова, М.A. Аматов, И.С. Кузнецова, С.А. Кунгурцев, Н.А. Чеканов // Экологические системы и приборы. — 2009. — № 7. — С. 31—40.
2.Аматова Г.М. Исследование модели взаимодействия трех популяций, связанных трофическими отношениями / Г.М. Аматова, М.A. Аматов, С.А. Кунгурцев // Экологические системы и приборы. — 2011. — № 12. — С. 41—54.
3.Аматов М.А Исследование математической модели динамики численностей трех взаимодействующих популяций / М.A. Аматов, Г.М. Аматова, И.С. Кузнецова // Вопросы современной науки и практики. Университет им. В.И. Вернадского. Тамбов, 2009. — С. 65—77.
4.Аматов М.А. Применение математического пакета MAPLE к интегрированию систем дифференциальных уравнений с кусочно-непрерывными правыми частями / М.A. Аматов, Г.М. Аматова, О.А. Ишкова, И.С. Кузнецова, Н.А. Чеканов // Вестник Херсонского национального технического университета. — 2009. — № 2(35). — С. 19—24.
5.Базыкин А.Д. Нелинейная динамика взаимодействующих популяций. Москва-Ижевск: РХД, 2003. — 367 с.
6. Ингеницкий И. Саранча. Энциклопедия Брокгауза и Эфрона [Электронный ресурс] / И. Ингеницкий. [Электронный ресурс] — Режим доступа. — URL: http://libbabr.com/?book=4571 (дата обращения: 04.01.2015).
7.Одум Ю. Экология в 2-х т. Т. 2 / Ю. Одум. М.: Мир, 1986. — 376 с.
дипломов


Оставить комментарий