ЧИСЛЕННОЕ ИССЛЕДОВАНИЕ МГД УПРАВЛЕНИЯ
СВЕРХЗВУКОВЫМ ПОТОКОМ В СРЕДЕ OPENFOAM

Ряховский Алексей Игоревич

аспират, кафедра «Высшая математика»,

Санкт-Петербургский Политехнический Университет,

РФ, г. Санкт-Петербург

E-mail: alexey.i.ryakhovskiy@mail.ioffe.ru

Шмидт Александр Александрович

д-р физ.-мат. наук, заведующий сектором численного моделирования,

Физико-технический институт им. А.Ф. Иоффе,

РФ, г. Санкт-Петербург

OPENFOAM NUMERICAL SIMULATION OF MHD SUPERSONIC FLOW CONTROL

Alexey Ryakhovskiy

рhd student, Department of Mathematics Saint-Petersburg Polytechnic University,

Russia, Saint-Petersburg

Alexander Schmidt

doctor of Physics and Mathematics, head of Numerical Modeling Department

Ioffe Institute,

Russia, Saint-Petersburg

АННОТАЦИЯ

Решена задача численного моделирования сверхзвукового обтекания твердого тела в форме конуса со скругленной вершиной при наличии постоянного магнитного поля. Задача решалась с использованием интегрированной среды численного моделирования OpenFOAM. На основе центральных разностных схем разработан солвер, позволяющий рассчитывать сверхзвуковые МГД течения в ограниченном диапазоне чисел Стюарта. Показана возможность управления формой ударной волны при помощи магнитного поля, генерируемого катушкой с током.

ABSTRACT

A numerical simulation of supersonic flow around a spherically blunted cone in presence of constant magnetic flied is carried out. The solution was obtained using OpenFOAM numerical simulation toolbox. The solver suitable for modeling supersonic MHD flows within limited range of Stuart number is developed based on the central difference schemes. The possibility of controlling a shock wave configuration with a magnetic field is demonstrated.

Ключевые слова: магнитная гидродинамика; управление потоком; свехзвуковые течения; численное моделирование; метод конечных элементов; центральные разностные схемы.

Keywords: magnetohydrodynamics; supersonic flows; numerical simulation; finite volumes method; central difference schemes.

Введение.

Проблема управления ударно-волновыми конфигурациями немеханическими способами является актуальной для аэрокосмического приборостроения. Термодинамические нагрузки, испытываемые летательными аппаратами при входе в атмосферу, могут привести к повреждению и в некоторых случаях даже разрушению дорогостоящего оборудования. Для решения данной проблемы было предложено несколько концепций, одной из наиболее перспективных среди которых является использование магнитного поля для воздействия на набегающий поток ионизованного газа [1]. Существуют также исследования по разработке систему искусственной ионизации газа в потоке для усиления интенсивности МГД взаимодействия [2]. В силу дороговизны и сложности соответствующих натурных экспериментов в данной области, математическое моделирование становится важным инструментом исследований. Проприетарные системы численного моделирования предлагают ограниченную функциональность для решения задач подобного типа, не предоставляя доступа к исходному коду солверов и термодинамических моделей. По этим причинам нами был сделан выбор в пользу открытой интегрированной платформы для численного моделирования OpenFOAM. Свободный доступ к коду этого инструментария позволяет модифицировать и дополнять имеющиеся солверы, давая возможность оптимизировать метод решения в зависимости от задачи.

Постановка задачи.

Рассматривается сверхзвуковое обтекание твердого тела в форме конуса с закругленной вершиной потоком слабо ионизированного газа. В качестве газа набегающего потока были рассмотрены воздух и CO₂, составляющие атмосферы Земли и Марса соответственно. Заданная температура потока 250 К-300 К является характерной для верхних слоев атмосферы. Скорость звука в таких условиях составляет приблизительно 250–300 м/c. Число Маха в расчетах находится в пределах 3–4. Внутри обтекаемого тела располагается катушка с током, создающая постоянное магнитное поле. Параметры создаваемого магнитного поля были взяты таким образом, чтобы модуль индукции в районе носа обтекаемого тела равнялся ~1 Тесла. Небольшое магнитное число Рейнолдса позволяет нам пренебрегать индуцируемым электрическим полем. Интенсивность МГД взаимодействия определяется Числом Стюарта (St) [3, с. 224], которое в нашей задаче принимает значения от 0 до 0.4.

Обтекаемое тело представляет собой конус со сферически закругленной вершиной. Радиус основания конуса – 1 м. Угол раствора – 120°.

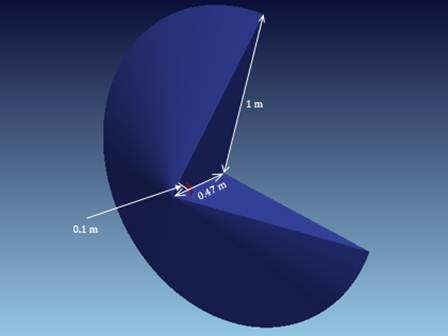
Рисунок 1. Геометрия обтекаемого тела

Таблица 1.

Термофизические параметры

Решается система уравнений магнитной гидродинамики для невязкого газа с условием постоянности магнитного поля.

                                                    (1)

В нашем случае F – объемная сила Лоренца, Q – мощность джоулева нагрева. Эти величины зависят от скорости потока и индукции магнитного поля.

Разработка солвера.

Стандартный инструментарий OpenFOAM предлагает несколько различных солверов для расчета сверхзвукового течения, однако, не все из них подходят для решения нашей задачи. Часть из них, например, sonicFoam и его модификации, решают систему уравнений Навье-Стокса в переменных скорость-давление (т. н. pressure based солверы). Такой подход сопряжен с появлением нефизических особенностей решения в области ударного слоя: главным образом появлением пиков профилей физических характеристик (т. н. overshoot). По этим причинам для нашей работы был выбран солвер rhoCentralFoam. Он относится к т. н. density based солверам, т. е. ищет решение системы в переменных скорость-плотность. Данный солвер основан на центральных разностных схемах Курганова и Тадмора [4]. При использовании rhoCentralFoam в нашей задаче без МГД взаимодействия были получены профили термофизических характеристик, качественно совпадающие с теоретическими ожиданиями.

Так как в стандартном наборе средств OpenFOAM отсутствует необходимый нам солвер для сверхзвуковых МГД течений сжимаемого газа, недостающие МГД слагаемые были добавлены нами в rhoCentralFoam. Разностные схемы для них были заимствованы из статьи Балбаса и Тадмора [5], в которой предложена МГД модификация для схем Курганова.

Численное решение.

В виду того, что рассматриваемый летательный аппарат имеет осевую симметрию, мы можем свести задачу к двумерной постановке. Расчетная область в таком случае представляет собой сектор цилиндра с вырезанным сектором обтекаемого тела. Вычислительная сетка сгущена в области носа обтекаемого тела для более точного расчета фронта ударной волны и эффекта МГД взаимодействия. При недостаточном (< 25) количестве расчетных ячеек по толщине ударного слоя наблюдаются нарушения гладкости рядом с границей, соответствующей обтекаемому объекту. Размерность использованной расчетной сетки: 576000 ячеек.

Для поиска стационарного решения в начальный момент времени задается однородное распределение скорости, температуры и плотности потока. На боковых сторонах сектора расчетной области для всех характеристик задается условие цилиндрической симметрии (wedge). На границах, соответствующих обтекаемому объекту заданы условия нулевой составляющей нормальной скорости (slip). При задании граничного условия для температуры на обтекаемом теле использовались два подхода. В первом случае задавалась постоянное значение температуры, что позволяло оценить влияние МГД взаимодействия на тепловой поток через границу. В другом случае ставилось условие нулевого потока и вычислялось значение температуры поверхности, с помощью которой можно было бы вычислить реальное значение теплового потока при наличии реального значения температуры объекта. На торцах расчетной области ставятся условия входа и выхода (inletOutlet).

Рисунок 2. Геометрия рассчетной области и граничные условия

Разработанный нами солвер является устойчивым при условии St < 0.25. Высокая интенсивности МГД взаимодействия (превышение локальным числом Стюарта в некоторых областях значения 0.35) приводит расхождению решения.

В результате проведенных расчетов были получены пространственные распределения термодинамических параметров потока. На представленных рисунках заметна разница между потоками в отсутствии и присутствии магнитного поля. Приведенные профили температуры и давления на передней поверхности обтекаемого тела демонстрируют понижение термофизических характеристик при наличии МГД взаимодействия, в особенности в областях, где модуль индукции генерируемого магнитного поля достигает наибольших значений.

Рисунок 3. Слева – распределение продольной скорости потока, справа – профили температуры на поверхности обтекаемого тела в присутствии и отсутствии магнитного поля

 Вид численно полученных профилей совпадает с теоретическими ожиданиями. Изменение расстояния между обтекаемым телом и фронтом ударной волны в присутствии магнитного поля также соответствует теоретической оценке [6].

Заключение.

В ходе исследования был разработан солвер для задач, связанных с МГД управлением сверхзвуковым обтеканием затупленных объектов. С помощью созданного солвера были полученные численные результаты для потоков с числом Маха 3–4, интенсивность МГД взаимодействия в которых не превышает . Была также продемонстрирована эффективность центральных разностных схем Балбаса-Тадмора в решении подобных задач. В будущем планируется сравнение рассмотренного подхода с другими способами решения, например, методами годуновского типа. Кроме того, необходимо усовершенствовать термофизическую модель и улучшить устойчивость разработанного солвера для обеспечения применимости к более широкому спектру задач.

Список литературы:

1. Jarvinen P.O. On the use of magnetohydrodynamics during high speed re-entry // Avco Research Note 463 – 1964.
2. Nishihara M. et al. MHD supersonic boundary layer control using pulsed discharge ionization // 43rd AIAA Aerospace Sciences Meeting and Exhibit. – 2005. – С. 2005.
3. Mitchner M., Kruger C. H. Partially ionized gases. – New York: Wiley, 1973. – Т. 8.
4. Kurganov A., Tadmor E. New high-resolution central schemes for nonlinear conservation laws and convection–diffusion equations // Journal of Computational Physics. – 2000. – Т. 160. – № 1. – P. 241–282.
5. Balbás J., Tadmor E., Wu C.C. Non-oscillatory central schemes for one-and two-dimensional MHD equations: I // Journal of Computational Physics. – 2004. – Т. 201. – № 1. – С. 261–285.
6. Farris M.H., Russell C.T. Determining the standoff distance of the bow shock: Mach number dependence and use of models // Journal of geophysical research. – 1994. – Т. 99. – № A9. – С. 17681.