Статья опубликована в рамках: XXXIV Международной научно-практической конференции «Личность, семья и общество: вопросы педагогики и психологии» (Россия, г. Новосибирск, 13 ноября 2013 г.)
Наука: Педагогика
Секция: Педагогика высшей профессиональной школы
Скачать книгу(-и): Сборник статей конференции, Сборник статей конференции часть II
- Условия публикаций
- Все статьи конференции
дипломов
ИСПОЛЬЗОВАНИЕ МЕТОДА МОЗГОВОГО ШТУРМА ПРИ ОБУЧЕНИИ СТУДЕНТОВ РЕШЕНИЮ ЗАДАЧ (НА ПРИМЕРЕ ТЕМЫ «ЛИНИИ ВТОРОГО ПОРЯДКА»)
Вакуленко Евгений Геннадьевич
преподаватель, Славянский сельскохозяйственный техникум, студент магистратуры, филиал Кубанского государственного университета, г. Славянске-на-Кубани,
Е-mail: sklifasik@gmail.com
Чернышева Ульяна Александровна
доцент, канд. пед. наук, Кубанский государственный университет, филиал в г. Славянске-на-Кубани
Е-mail:
USE OF BRAINSTORMING AT TRAINING OF STUDENTS IN THE SOLUTION OF TASKS (ON THE EXAMPLE OF THE SUBJECT «LINES OF THE SECOND ORDER»)
Vakulenko Evgeny Gennadevich
teacher, Slavyansk agricultural technical school, Slavyansk-on-Kuban student of a magistracy, branch of the Kuban state university in Slavyansk-on-Kuban
Tchernysheva Uliana Alexandrovna
associate professor, candidate of pedagogical sciences, branch of the Kuban state university in Slavyansk-on-Kuban
АННОТАЦИЯ
Статья посвящена применению метода мозгового штурма при обучении студентов математике. Рассмотрено соответствие этапов организации метода мозгового штурма классическим этапам решения математических задач. Приведен пример применения метода при организации обучения студентов решению конкретной задачи по теме «Линии второго порядка». Статья полезна студентам и преподавателям.
ABSTRACT
Article is devoted to application of brainstorming at training students in mathematics. Compliance of stages of the organization of a method of brain storm to classical stages of the solution of mathematical tasks is considered. The example of application of a method is given at the organization of training of students to the solution of a specific task of the subject "Lines of the Second Order". Article is useful to students and teachers.
Ключевые слова: метод мозгового штурма; студенты; обучение; решение задач; линии второго порядка.
Keywords: brainstorming; students; training; solution of tasks; lines of the second order.
Одной из эффективных технологий решения нестандартных задач является метод мозгового штурма. Метод мозгового штурма — это оперативный метод решения проблемы на основе стимулирования творческой активности, при котором участникам обсуждения предлагают высказывать как можно большее количество вариантов решения, в том числе самых фантастичных. Затем из общего числа высказанных идей отбирают наиболее удачные, которые могут быть использованы на практике.

Рисунок 1. Соответствие между этапами мозгового штурма и классическими этапами решения задачи
Этапы проведения мозгового штурма вполне согласуются с этапами классических схем решения задачи по Фридману и Пойа (см. рис. 1).
Метод мозгового штурма подразумевает поиск решения нестандартной задачи, но чаще всего нестандартные задачи сводятся к ряду ключевых задач, которые решаются по определенному алгоритму.
Рассмотрим методику организации обучения студентов решению задач, в основу которой положены технология алгоритмизации и метод мозгового штурма, на примере темы «Линии второго порядка».
На первом этапе нами были выделены ключевые задачи по теме и проведена их классификация (см. рис. 2).

Рисунок 2. Классификация задач по теме «Линии второго порядка»
Далее были составлены блок-схемы и алгоритмические предписания для решения этих задач методом алгоритмизации.
Обучив студентов решению ключевых задач по алгоритмам, необходимо переходить к задачам более высокого уровня сложности. Метод мозгового штурма, как уже было сказано выше, хорошо подходит для решения такого рода задач. При использовании этого метода происходит стимуляция мыслительной деятельности студентов, повышается их интерес к предмету.
Первые два этапа организации решения проблемы методом мозгового штурма, объявление правил и разминка, занимают немного времени, но играют большую роль в подготовке к мозговому штурму. Когда студенты полностью готовы узнать задачу, которую им предстоит решить, можно приступить к основному процессу проведения мозгового штурма. Желательно формулировку задачи раздать каждому на листе, чтоб у каждого возникло чувство ответственности, что это именно его задача и только от него зависит исход её решения. Если нет такой возможности, то можно написать формулировку задачи на доске или на большом листе бумаги. Оценка и выбор идей — самый важный этап проведения штурма. Необходимо отказываться от неоптимальных вариантов решения задачи и оставлять самые лучшие идеи, из которых можно составить план решения нестандартной задачи.
Проиллюстрируем пример применения метода мозгового штурма при решении конкретной задачи. Рассмотрим, например, такую задачу.
Постановка задачи
Составить уравнение гиперболы, зная уравнения ее асимптот: ![]() и уравнение одной из ее касательных:
и уравнение одной из ее касательных: ![]() .
.
Продвижение идеи.
1. После пятиминутного размышления над решением задачи, каждый по очереди начинает говорить свою оригинальную идею для решения задачи или её части. Так как ![]() — асимптоты, то
— асимптоты, то ![]() , откуда
, откуда ![]() .
.
Если среди высказанных на 1-ом круге идей нет подходящей мысли для начала решения данной задачи, учителю следует дать направление для размышления; подсказка может быть такой: «Какие параметры гиперболы можно найти, зная уравнения её асимптот», и снова следует дать возможность по очереди каждому высказаться. Как только студенты поймут, что необходимо найти отношение полуосей, то переходим ко 2-му кругу высказывания идей.
2. На 2-ом круге студенты должны прийти к выводу, что нужно найти точки касания — общие точки гиперболы и касательной. Уравнение касательной к эллипсу имеет вид ![]() , откуда
, откуда ![]() , где точки
, где точки ![]() — координаты точки касания.
— координаты точки касания.
3. На 3-ем круге, учитывая, что по условию касательная имеет уравнение ![]() нужно определить зависимость между координатами точки касания и параметрами гиперболы. Сравнив два уравнения одной и той же касательной, получим:
нужно определить зависимость между координатами точки касания и параметрами гиперболы. Сравнив два уравнения одной и той же касательной, получим: ![]() . С учетом что
. С учетом что ![]() , можно выразить координаты так:
, можно выразить координаты так: ![]() .
.
4. На 4ом круге – требуется обосновать идею подстановки найденных значений ![]() и
и ![]() в уравнение гиперболы, после чего получим:
в уравнение гиперболы, после чего получим:

Тогда ![]() . Отсюда уравнение гиперболы: х2/4 – y2 = 1 .
. Отсюда уравнение гиперболы: х2/4 – y2 = 1 .
Запись ответа
Уравнение гиперболы заданной ее асимптотами ![]() и уравнением одной ее касательной
и уравнением одной ее касательной ![]() имеет вид: х2/4 – y2 = 1.
имеет вид: х2/4 – y2 = 1.
Решение задачи можно проверить в разработанной нами средствами Delphi программе «Решение задач о линиях второго порядка» (рис. 3).
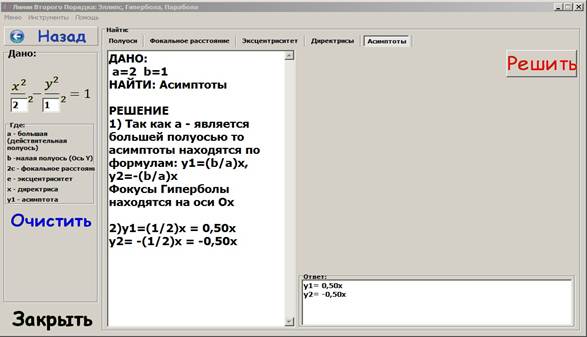
Рисунок 3. Проверка решения посредством программы «Решение задач о линиях второго порядка»
Далее полезно продемонстрировать студентам рисунок к данной задаче, выполненный с помощью программного пакета Maple 5 (рис. 4).

Рисунок 4. Рисунок к задаче, выполненный посредством Maple 5
Практическая значимость разработанных методических рекомендаций для проведения занятий заключается в том, что они могут найти прямое применение на практике, и не только при обучении студентов теме «Линии второго порядка», но и при изучении других разделов математики. Как показала проведенная нами апробация, применение описанной методики приводит к повышению эффективности обучения студентов решению задач.
Список литературы:
1.Гин А.А. Бескровная Атака. Технологии проведения учебного мозгового штурма / А.А. Гин // Педагогика + ТРИЗ. — № 3. Мн. : ПолиБиг, 1997. — 64 с.
2.Пойа Д. Как решать задачу: пособие для учителей / пер. с англ. В. Звонарёвой, Д. Белла; под ред. Ю. Гайдука. 2-е изд. М.: Учпедгиз, 1961. — 207 с.
3.Сборник задач по геометрии : учеб. пособие для студ. физ.-мат. фак. пед. ин-тов. В 2-х ч. Ч. 2. / Под. ред Л.С. Атанасяна. М. : Просвещение, 1975. — 176 с.
4.Фридман Л.М. Как научиться решать задачи: книга для учащихся старших классов средней школы / Л.М. Фридман, Е.Н. Турецкий. 3-е изд., дораб. М.: Просвещение, 1989. — 192 с.
дипломов


Оставить комментарий