ПОСТРОЕНИЕ  СИСТЕМ  УПРАВЛЕНИЯ  С  ПОВЫШЕННЫМ  ПОТЕНЦИАЛОМ  РОБАСТНОЙ  УСТОЙЧИВОСТИ  ДЛЯ  ОБЪЕКТОВ  С  ОДНИМ  ВХОДОМ  И  ОДНИМ  ВЫХОДОМ

Галимова  Ризагуль  Фаритовна

магистр  2  курса  Евразийского  национального  университета  им.  Л.Н.  Гумилева,  Республика  Казахстан,  г.  Астана

Email:rizagul1990@mail.ru

Сатыбалдина  Дана  Каримтаевна

канд.  техн.  наук,  доцент  Евразийского  национального  университета  им.  Л.Н.  Гумилева,  Республика  Казахстан,  г.  Астана

В  настоящее  время  наиболее  актуальной  в  современной  теории  управления  является  проблема  построения  робастных  систем  управления.  Большое  внимание  уделяется  построению  регуляторов,  обеспечивающих  системы  автоматического/автоматизированного  управления  робастной  устойчивостью  и/или  робастностью  по  качеству.  Большинство  реальных  систем  автоматического  управления  на  данный  момент  функционирует  в  условиях  той  или  иной  неопределенности  параметров  объекта  и  дрейфа  их  характеристик  в  больших  пределах  [3,  5,  6].  Таким  образом,  возникает  необходимость  в  разработке  моделей  и  методов  анализа  и  синтеза  систем,  имеющих  неограниченно  расширяемую  область  устойчивого  движения  при  наличии  внешних  и  внутренних  возмущений. 

В  данной  статье  предложены  методы  построения  систем  управления  с  повышенным  потенциалом  робастной  устойчивости  в  классе  трехпараметрических  структурно-устойчивых  отображений  (катастрофа  ласточкин  хвост)  для  объектов  с  одним  входом  и  одним  выходом.  Для  исследования  устойчивости  нами  была  использована  линейная  аппроксимация  и  алгебраический  критерий  Гурвица  [1,  2].

Предположим,  что  система  управления  обладает  единственным  входом  и  единственным  выходом  и  имеет  скалярный  закон  управления  и  описывается  уравнением  состояния  в  стандартной  форме: 

                                         (1)

где 

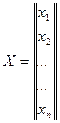
Закон  управления    представим  в  форме  трёхпараметрических  структурно-устойчивых  отображений  (катастрофа  ласточкин  хвост) 

                (2)

Систему  (1)  в  развернутом  виде  можно  записать  следующим  образом:        

      (3)

Стационарные  состояния  этой  системы  можно  определить  решением  уравнения:

                               (4)

Где  из  (4)  можно  получить  стационарные  состояния: 

        (5)

Другие  стационарные  состояния  имеют  вид  [3,  6]:

  (6)

При  :  два  вещественных  корня,  если  ,  и  ни  одного  вещественного  корня,  если  ;

При  :  два  вещественных  корня,  если  ,  четыре  вещественных  корня,  если    и  ни  одного  вещественного  корня,  если  .

при  (7)

  при    (8)

Исследование  устойчивости  данных  стационарных  состояний  (6),(7),(8)  проводится  на  основе  линейной  аппроксимации  [5]  и  алгебраического  критерия  Гурвица.  Для  этого  необходимо  разложить  нелинейные  члены  в  системе  уравнений  (3)  вокруг  стационарных  состояний    и,  ограничиваясь,  членами  первого  приближения  получим                          

  (9)

Дифференциальному  уравнению  (9)  соответствует  характеристическое  уравнение 

,                (10)

где 

Воспользовавшись  критерием  Гурвица  можно  получить  условия  устойчивости  стационарных  состояний  (6),(7),(8).  Для  этого  построим  матрицу  Гурвица  и  определители  Гурвица.

                                         (11)

    ,        ,             (12)

Для  выполнения  условия  устойчивости  по  Гурвицу  [5]  и  следовательно,  для  того  чтобы  вещественные  части  всех  корней  характеристического  уравнения  (10)  имели  отрицательный  знак  необходимо  и  достаточно,  чтобы  все  n  диагональных  миноров  (12)  матрицы  Гурвица  (11)  были  положительными.  Это  означает,  что 

В  свою  очередь,  характеристическое  уравнение  для  состояния  (5)  приобретает  вид: 

                                (13)

Рассмотрим  условия  положительности  диагональных  миноров  определителя  Гурвица  (11)  характеристического  уравнения  (13)  для  системы  1-го,  2-го,  3-го  и  n-го  порядков.

При    т.е.  .

При    условия  устойчивости    т.е.  .

При    матрица  Гурвица  записывается  в  виде:

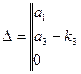
Условия  устойчивости: 

При    второе  и  третье  условия  будут  выполняться,  если    при  любом  изменении    в  пределах  .  Далее  можно  рассмотреть  устойчивость  стационарного  состояния  (5)  для  системы  n-го  порядка,  изначально  предполагая,  что  .  Коэффициенты  характеристического  уравнения:  .

Условия  устойчивости:    при    т.е. 

Рассмотрим  условия  устойчивости  стационарного  состояния  (6),  лежащие  на  поверхности  сепаратрисы.  При  этом  характеристическое  уравнения  преобразуются  к  виду: 

Условия  устойчивости  стационарного  состояния  (6)  получим,  построив  матрицу  Гурвица.

В  ходе  исследования  устойчивости  стационарного  состояния  (6),  эти  точки  являются  точками,  лежащими  на  поверхности,  образующие  сепаратрису  катастрофы,  которые  делят  пространство  на  открытые  области  с  качественным  одинаковым  поведением,  где  характеристическое  уравнение  преобразуется  также  к  виду:,  так  как  величина  .

На  основании  вышеизложенного  можно  сделать  следующий  вывод,  что  устойчивость  системы  на  поверхности,  образующей  сепаратрису  катастроф  от  управлений  не  зависит  и  непосредственно  определяется  устойчивостью  или  неустойчивостью  линейного  объекта  управления  при  заданных  значениях  параметров  объекта  управления.

Далее  исследуем  устойчивость  стационарных  состояний  (7),  где  характеристическое  уравнение  принимает  вид: 

                          (14)

Рассмотрим  условия  положительности  диагональных  миноров  определителя  Гурвица  (11)  для  характеристического  уравнения  (14)  для  системы  1-го,  2-го.  3-го  и  n-го  порядков  при  . 

При      т.е.    

При  .  Условия  устойчивости    и    т.е.  ,    или 

При  .  В  этом  случае,  матрица  Гурвица  записывается  в  виде:

Условия  устойчивости:

В  результате  всех  вышеизложенных  вычислений,  приходим  к  выводу,  что  система  управления  с  единственным  входом  и  единственным  выходом  со  скалярным  законом  управления  заданным  в  форме  трехпараметрических  структурно-устойчивых  отображений  (катастрофа  ласточкин  хвост)  позволяет  увеличить  область  робастной  устойчивости.

Список  литературы:

1.Ашимов  А.А.,  Бейсенби  М.А.  Структурно-устойчивые  отображения  в  построении  систем  управления  с  повышенным  потенциалом  робастной  устойчивости.  //  Труды  международной  конференции  «Проблемы  информатики  и  управления»,  Бишкек,  19—22  сентября  2000  г.,  —  с.  147—152.

2.Бейсенби  М.А.,  Ержанов  Б.А.,  Системы  управления  с  повышенным  потенциалом  робастной  устойчивости.  Астана:2002,  —  164  с.

3.Бесекерский  В.А.,  Небылов  А.В.  Робастные  системы  автоматического  управления.  Москва:  Наука,  1983  —  239  с.

4.Гильмор  Р.  Прикладная  теория  катастроф.  М.:  Мир,  1981. 

5.Техническая  кибернетика.  Теория  автоматического  регулирования.  //  Под  ред.  В.В.  Солодовникова.  М.:  Машиностроение.  Кн.  1.  1967.  —  768  с.

6.Томпсон  Дж.,  Майкл  Т.  Неустойчивости  и  катастрофы  в  науке  и  технике.  М.:  Мир,  1985  —  254  с.