Статья опубликована в рамках: LIV Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 25 января 2016 г.)
Наука: Технические науки
Секция: Строительство и архитектура
Скачать книгу(-и): Сборник статей конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
НОВЫЙ ПОДХОД В ТЕОРИИ ДЕФОРМАЦИИ БАЛКИ
Алдабергенов Абай Капанович
канд. техн. наук, проф. кафедры Энергетики и машиностроения
Костанайского инженерно-экономического университета,
Республика Казахстан, г. Костанай
E-mail: al.abai.41@mail.ru
NEW APPROACH IN THE THEORY OF DEFORMATION OF BEAMS
Abai Aldabergenov
сandidate of Technical Sciences
professor of the Department of Энергетики и Mechanical Engineering
of Kostanai Engineering-Economic University,
Kazakhstan, Kostanai
АННОТАЦИЯ
В работе впервые выведены универсальные формулы для определения констант интегрирования. Утверждение о том, что для балок с большим числом участков применение метода непосредственного интегрирования считается неудобным, опровергается. Это – научная новизна работы.
ABSTRACT
In work for the first time derived universal formulas to determine the constants of integration. The statement that for beams with a large number of plots application of the method of direct integration is disproved. It is a scientific novelty of the work.
Ключевые слова: балка; деформация; изгиб; уравнение; нагрузка.
Keywords: beam; deformation; bending; the equation; load.
На сегодня решение дифференциального уравнения изогнутой оси балки
(![]() ) [1, с. 205]:
) [1, с. 205]:
![]() –
– ![]() (1)
(1)
проводится двумя известными методами: метод непосредственного интегрирования и метод начальных параметров. Как известно, для балок, состоящих из большого числа участков, число постоянных интегрирования будет велико и вычисления их сопряжены со значительными трудностями. Поэтому считается, что применение первого метода в этих случаях неудобным. Сведения объема вычислительных работ к минимуму всегда является актуальной проблемой. Она требует дополнительного исследования. В данной работе будет показано, что указанные выше трудности сильно преувеличены. Для уменьшения числа постоянных интегрирования до двух был предложен второй метод. Особенностью этого метода является то, что его универсальные уравнения получены со вводом дополнительных условий [2, с. 339]. Любой метод, полученный с вводом каких бы то ни было условий надо считать некорректным подходом. Следовательно, по методу начальных параметров остаются вопросы относительно обоснованности ввода этих дополнительных условий.
Рассмотрим балку, показанную на рисунке 1. Начало координат общее для всех участков поместим на левом конце балки.

Рисунок 1. Изгиб балки
Выражения изгибающих моментов на участках балки запишутся так:
![]() ;
; ![]() ;
;  ;
;
![]() ;
; ![]() . (2)
. (2)
После интегрирования уравнения (1), записанного с учетом (2), для отдельных участков будем иметь:
а) ![]() ; б)
; б) ![]()
в) ![]() ;
;
г)  ;
;
д) ![]() . (3)
. (3)
Для определения постоянных интегрирования используем условия задачи в местах гладкого и непрерывного сопряжения участков:
1) при х = 0 ![]() ; 2) при х = а
; 2) при х = а ![]() ; 3) при х = в
; 3) при х = в ![]() ;
;
4) при х = с ![]() . 5) при
. 5) при ![]()
![]() . (4)
. (4)
Из условий (4) с учетом (3) находим:
![]() ;
; ![]() ;
;  ;
;
 ;
; 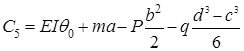 . (5)
. (5)
Обратите особое внимание на формулу для определения постоянного интегрирования последнего участка (5). В ней полностью сохранены формулы для определения константов предыдущих участков. Это означает, что постоянные данного участка можно найти из формулы последнего участка, учитывая лишь левые от него силы. Поэтому ее назовем универсальной формулой для постоянных интегрирования. При этом все эти постоянные выражаются через константу (угол поворота) первого участка. Таким образом, остается неизвестным единственная постоянная ![]() . После анализа формул системы (5) можно их обобщить и в общем виде записать так:
. После анализа формул системы (5) можно их обобщить и в общем виде записать так:
 , (6)
, (6)
где: ![]() номер участка, для которого определяется постоянное интегрирования;
номер участка, для которого определяется постоянное интегрирования; ![]() номер нагрузки. Правильность этой формулы подтверждена на случаях, когда на балку действуют несколько сосредоточенных моментов, сил и распределенных нагрузок.
номер нагрузки. Правильность этой формулы подтверждена на случаях, когда на балку действуют несколько сосредоточенных моментов, сил и распределенных нагрузок.
Внося значения постоянных (5) в уравнения (3),получим:
a) ![]() ; б)
; б) ![]() ;
;
b) ![]() ;
;
c) ![]() ;
;
d) ![]()
 . (7)
. (7)
Проинтегрируем систему уравнений (7) еще раз. Появятся дополнительно пять постоянных ![]() .
.
![]() ;
;
![]() ;
;
 ;
;

![]() ;
;

 .
.
Используя условия на стыках участков находятся постоянные![]() . Не повторяя рассуждений, совершенно аналогичных тем, какие были высказаны при нахождении постоянных
. Не повторяя рассуждений, совершенно аналогичных тем, какие были высказаны при нахождении постоянных ![]() , запишем:
, запишем:
 . (9)
. (9)
Замечено, что между постоянными интегрирования отдельных участков существует строгая взаимосвязь. А в формулах для определения постоянных интегрирования (6) и (9) наблюдаются устойчивые закономерности: а) в формулах для данного участка полностью сохраняются нагрузки предыдущих участков; б) каждый вид нагрузки входит в эти уравнения в виде слагаемого определенного типа; в) в формулах содержатся только те силы, которые расположены на левее рассматриваемого участка. В практических расчетах нет необходимости в вычислении этих коэффициентов. Например, после ввода констант ![]() по формуле (5) в уравнения (3) они сами упорядочатся и в окончательных уравнениях остается только постоянное
по формуле (5) в уравнения (3) они сами упорядочатся и в окончательных уравнениях остается только постоянное ![]() .
.
Таким образом, в работе получены универсальные формулы для определения констант интегрирования (6) и (9). По этим формулам можно вычислить постоянные интегрирования любого уравнения (участка). При любом количестве участков балки число постоянных будет равно двум (по деформациям) ![]() и
и ![]() , что сильно облегчает решение задачи. Отсюда следует, что методом непосредственного интегрирования можно пользоваться для любой балки, не зависимо от количества участков. Такое утверждение приводится впервые, и, по мнению автора, может быть рассмотрено, как научное открытие (научная новизна).
, что сильно облегчает решение задачи. Отсюда следует, что методом непосредственного интегрирования можно пользоваться для любой балки, не зависимо от количества участков. Такое утверждение приводится впервые, и, по мнению автора, может быть рассмотрено, как научное открытие (научная новизна).
Список литературы:
1. Алдабергенов А.К. Сопротивленире материалов с основами теории упругости. – Алматы: Рауан, 1994. – 468 с.
2. Писаренко Г.С. Сопротивление материалов. – Киев: Из-во тех. литературы,1963. – 792 с.
дипломов


Оставить комментарий