ЗАДАЧИ УПРАВЛЕНИЯ КОСМИЧЕСКИМ АППАРАТОМ С СОЛНЕЧНЫМ ПАРУСОМ

PROBLEMS OF SOLAR SAIL SPACECRAFT CONTROL

Elena Polyakhova

candidate of Physical and Mathematical Sciences, Assistant Professor, Saint-Petersburg State University,

Russia, Saint-Petersburg

Vladimir Korolev

candidate of Physical and Mathematical Sciences, Assistant Professor,

Saint-Petersburg State University,

Russia, Saint-Petersburg

Работа выполнена при финансовой поддержке Программы проведения фундаментальных исследований СПбГУ по приоритетным направлениям (грант 6.37.341.2015).

АННОТАЦИЯ

Специфика управления солнечным парусом космического аппарата состоит во взаимосвязи поступательного и вращательного движений всей конструкции. Чтобы управлять движением, необходимо менять размеры или ориентацию паруса относительно потока солнечных лучей.

ABSTRACT

Specificity of solar sail spacecraft control is in conjunction of its translational and rotational motions. To control the movement of the spacecraft, it is necessary to change the size or orientation of the sail in the sunlight flow.

Ключевые слова: космическая динамика; световое давление; солнечный парус; управление.

Keywords: spaceflight dynamics; radiation pressure; solar sail; control.

Принцип движения космических аппаратов (КА) под солнечным парусом базируется на эффекте светового давления, который открыл и измерил экспериментально П.Н. Лебедев в 1899 г. Впервые гипотеза о световом давлении была высказана еще Кеплером для объяснения отклонения хвостов от ядра кометы, пролетающей вблизи Солнца. Сама возможность использовать этот эффект для космических полётов была выдвинута Ф.А. Цандером [20] в 1924 г. Он рассмотрел конструкции солнечных парусов и пытался разработать основы теории движения в космосе таких объектов [1; 13; 15].

Пусть парус представляет собой зеркало, которое обладает идеальными свойствами [18]. Установим его в плоскость, перпендикулярную солнечным лучам. Тогда сила давления светового потока направлена вдоль излучения. Набегающие фотоны дважды обменяются импульсом с парусом: при поглощении и при излучении обратно. Зеркало в свою очередь передаёт это силовое воздействие КА.

Если повернем плоский зеркальный парус (рис. 1) под углом  к лучам потока, то импульс, передаваемый солнечному парусу со стороны фотонов, будет направлен перпендикулярно светоотражающей поверхности. Часть импульса, направленную параллельно парусу, фотоны сохранят у себя, так что парусу достанется меньше, чем при полном раскрытии к лучам. Величина светового давления упадет, а направление давления будет совпадать с нормалью к парусу, отложенной с теневой его стороны.

Если солнечный парус сделан из черного материала, то его тяга оказывается в два раза меньше идеально зеркального. Вдобавок в этом случае сила будет направлена не по нормали к поверхности, а по направлению потока солнечных лучей. Реальный парус отражает лишь часть падающих на него лучей, поэтому его эффективность лежит между идеальным и черным парусами, а также зависит от его положения.

Поворачивая парус, мы получаем возможность управлять направлением вектора тяги [1; 2; 19; 24]. Однако за это приходится платить ее величиной, так как если нормаль плоского паруса перпендикулярна потоку лучей, то парус вообще не даст никакой тяги. Ускорение, которое сообщает КА поток солнечных лучей, зависит также от отношения площади паруса к массе всей конструкции.

Рисунок 1. Формирование силы светового давления на солнечный парус

В силу своей специфики солнечный парус может использоваться прежде всего для полетов в околосолнечном пространстве. Раскрытие паруса на круговой гелиоцентрической орбите приведет к тому, что световое давление частично скомпенсирует притяжение Солнца. Это дает основание говорить о математической модели фотогравитационного поля [10; 18]. Например, для ускорения 1 мм/с² на расстоянии Земли от Солнца космическому аппарату массой 500 кг потребуется парус площадью 5 гектаров в полном раскрытии к лучам. Для сравнения отметим, что гравитационное притяжение к Солнцу дает ускорение на орбите Земли 6 мм/с². Масса паруса должна входить в те самые 500 кг общей массы спутника. Можно использовать полиэфирную пленку с коэффициентом отражения 0,85 при соответствующем напылении [15].

Если космический аппарат со сложенным солнечным парусом уже доставлен на орбиту движения вокруг Земли или Солнца, то его раскрытие обеспечит КА практически неограниченным запасом энергии. Однако у паруса есть один недостаток: в отличие от реактивных двигателей, мы не можем использовать его тягу в любом направлении с одинаковой эффективностью. Необходимо ориентировать парус специальным образом так, чтобы добиться желаемого изменения параметров орбиты. Повернув парус под углом, чтобы фотоны отскакивали назад относительно направления орбитального движения, мы получим небольшую силу, постепенно ускоряющую КА, то есть сможем двигаться по раскручивающейся спирали. При развороте паруса в другую сторону получим торможение и уменьшение расстояния до Солнца.

Чтобы изменить наклон плоскости орбиты КА, необходимо направить отражаемый солнечный лучик перпендикулярно начальной плоскости. Кроме того, вытянутую эллиптическую орбиту можно повернуть, изменяя долготу перицентра относительно центрального тела, чтобы сделать ее ближе к орбите астероида или кометы, встречи с которыми необходимо осуществить [5; 27].

Еще более интересные маневры можно выполнять с помощью солнечного паруса в околоземном пространстве. Направление светового излучения в этом случае не совпадает с направлением на центр притяжения. В течение года Земля совершает полный оборот относительно Солнца. Запасаясь терпением, можно дождаться оптимального для маневра времени года и перевести КА с помощью паруса на желаемую орбиту.

Первые практические разработки солнечного парусника были начаты в семидесятых годах ХХ века. Намечавшаяся на 1986 год перспектива полета КА под солнечным парусом для встречи с кометой Галлея не состоялась. Основная трудность состояла в упаковке гигантского полотнища в контейнер для вывода в космос и развертывания в рабочее положение уже на орбите. Позднее была признана удачной конструкция разрезного паруса наподобие вертолетного винта, каждая лопасть которого раскатывается из контейнера радиально. Благодаря многочисленным разработкам можно выбирать из огромного разнообразия моделей парусов (рис. 2). Это сплошные пленочные паруса (круглые, квадратные, веерные), паруса-парашюты, надувные баллоны, паруса типа вертолетного винта, лепестковые паруса типа «ромашки» и «подсолнуха», паруса сотовой конструкции на базе отдельных зеркальных модулей, системы пленочных передаточных зеркал и другие.

Отметим три основных проблемы:

·     развертывание паруса большой площади в рабочее положение,

·     жесточайший лимит на полную массу корабля с парусом,

·     обеспечение требуемой ориентации паруса в полете.

Только при условии разрешения всех проблем можно говорить о реальности космической миссии. При этом необходимо обеспечить достаточно сложное управление самим парусом, изменяя нужным образом его положение.

Эффективность обычных парусов всегда связана с углом их ориентации по отношению к лучам. В системе зеркал можно устанавливать такой ход лучей, чтобы направления падающего и отраженного световых потоков мало зависели друг от друга.

Рисунок 2. Разнообразие моделей парусов

Специфика управления солнечным парусом состоит во взаимосвязи поступательного и вращательного движений всей конструкции [9; 23]. Чтобы управлять тягой, необходимо менять ориентацию паруса, что требует работы микродвигателей. Самой выгодной представляется конструкция паруса, которая сама обеспечивала бы контроль за установкой нужной ориентации и управление для ее сохранения. В этом плане одним из перспективных вариантов солнечного паруса является двухстворчатая конструкция, предложенная с участием одного из авторов статьи [13–15]. Построив такое двухстворчатое зеркало паруса определенных пропорций (рис. 3), мы получим саморегулирующуюся по ориентации на Солнце конструкцию.

Силы давления  светового потока пропорциональны площади  поверхности элемента паруса и коэффициенту отражения . Они зависят от расстояния  до Солнца и направления вектора нормали  к поверхности элемента

                                                  (1)

Устойчивость обеспечивают моменты сил (1) относительно центра масс, которые меняют величину при малых отклонениях от нужного направления

.                                                      (2)

Главный вектор момента (2) сил давления, действующих на все элементы, будет отличен от нуля, если элементы имеют разные площади или углы относительного расположения. Это определяет возможность возврата в нужное направление или использование для разворота и создания нового расположения основного корпуса КА для ориентации в нужном направлении. Расположение элементов относительно корпуса можно менять с помощью двигателей, если поддерживать их работоспособность на основе солнечных батарей.

Рисунок 3. Схема расположения управляемой конструкции

Решение перечисленных проблем открывает интересные перспективы. Разумно управляя солнечным парусом, можно разогнать КА около Земли до второй космической скорости и выйти в межпланетное пространство для космического путешествия [1; 5; 6; 13; 27]. Маневры, которые космический аппарат может выполнить с помощью солнечного паруса, достаточно разнообразны. Однако, они повторяют спектр маневров, которые осуществимы с помощью других двигательных установок. Представляют интерес уникальные свойства парусов. К ним следует отнести возможность функционирования паруса в околосолнечных областях, где он одновременно может играть роль не только энергетической установки, но и экрана, который защищает приборный отсек от перегрева. Такая конструкция окажется незаменимой для проведения исследования физики околосолнечного пространства [24] и наблюдения за солнечными пятнами с близкого расстояния.

Имеется также возможность создания орбиты, синхронной с осевым вращением Солнца, то есть гелиосинхронной орбиты. Раскрытие паруса КА при этом уменьшит притяжение и спутник зависает над солнечным пятном по аналогии с полетом геостационарного над одной и той же точкой Земли. Возрастание эффективности солнечного паруса при приближении к Солнцу позволяет считать его перспективным на таком маршруте.

Что касается околоземных космических маневров, то здесь возможности еще более разнообразны. Например, уникальная роль паруса может состоять в его применении как сборщика космического мусора и техногенных отходов с околоземных спутниковых орбит. Проблема очистки орбит давно уже является актуальной. На геостационарной орбите плотность размещения приближается к критической, но КА с солнечным парусом сможет оказать неоценимую услугу по ее очистке, чтобы спутники не мешали друг другу работать. Специальный космический аппарат сможет забирать в контейнер спутник с густо населенной орбиты для доставки на другую, которая пока более свободна. Другой вариант применения предполагает возможность передать или прикрепить аналог парашюта, который будет ускорять сход с орбиты для прекратившего работу КА благодаря торможению при действии потока света и усилит сопротивление атмосферы уже на больших расстояниях до поверхности Земли.

Еще более успешной и полезной может быть использование солнечного паруса для вывода КА на геосинхронную стационарную широтную орбиту и дальнейшего устойчивого функционирования (рис. 4). Плоскость такой орбиты параллельна плоскости экватора, но находится на ненулевой широте.

Рисунок 4. Геосинхронная стационарная широтная орбита

На таких широтных орбитах можно формировать новые комплексы для размещения спутниковых систем теле- или радиосвязи. После создания солнечного паруса, который сможет успешно функционировать на орбите сколь угодно долго, можно предусмотреть возможность замены для обновления некоторых элементов аппаратуры при обслуживании системы КА [5; 6].

Технология крупногабаритных конструкций отражателей солнечного света в сторону поверхности Земли только зарождается [15]. Зато перспективы таких орбитальных устройств заманчивы. Солнечные рефлекторы смогут вечером и ночью освещать большие города (рис. 5). Не меньше нуждаются в освещении заполярные регионы, населенность которых достаточно велика. Добрую службу в будущем может сослужить отраженный свет и в случае стихийных бедствий (землетрясений, наводнений или крупных аварий), когда космическое освещение будет играть не менее важную роль, чем оперативная связь, осуществляемая сегодня с помощью спутников.

Рисунок 5. Использование отражателей солнечного света

Создание полноценного солнечного парусника остается делом будущего. Для этого потребуются сложные конструкторские решения и космические технологии [1]. Особой задачей становится управление КА с использованием солнечного паруса в качестве двигательных установок малой тяги.

Теория оптимального управления приводит к сложным задачам решения дополнительно полученных уравнений математических моделей, которые могут использовать принцип максимума Понтрягина или уравнение Беллмана для различных условий. Существуют аналитические и численные методы исследования, которые получают точные или приближенные решения [6; 8; 10].

Уравнения движения КА в центральном гравитационном поле с учетом возмущений могут быть записаны в различном виде при выборе декартовых, сферических или цилиндрических координат, кеплеровых элементов или канонических переменных. В случае движения при сохранении начальной плоскости орбиты можно также использовать полярные координаты :

                                  (3)

Здесь  – радиальная и трансверсальная компоненты ускорения, которые зависят от закона управления  углом установки элементов паруса по отношению к потоку солнечных лучей и величины удельного давления света  на соответствующем удалении от Солнца.

Алгоритмы управления многочисленны и разнообразны, так как они определяются параметрами начальной и конечной орбит или назначением маневра. Движение в центральном гравитационном поле имеет решение, которое при отсутствии возмущающих сил определяется начальными значениями радиус-вектора, вектора скорости и гравитационным параметром центрального тела. Они определяют постоянные параметры орбиты, которые называются кеплеровыми элементами . Здесь перечислены: большая полуось , эксцентриситет эллипса , наклон плоскости орбиты , долгота восходящего узла , долгота перицентра  и средняя аномалия  в начальный момент времени . Кеплеровы элементы орбиты для возмущенного движения КА будут функциями времени, которые называют оскулирующими элементами.

Это позволяет вычислять декартовы координаты  и скорости  в абсолютной системе координат для невозмущенного движения в произвольный заданный момент времени  с учетом обозначений

                                      (4)

по формулам [4; 2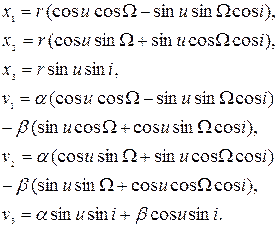5]

                               (5)

Время движения между двумя точками орбиты можно определить из последнего уравнения (4), которое называют уравнением Кеплера. Для нахождения изменений оскулирующих элементов возмущенного движения можно использовать дифференциальные уравнения Эйлера

              (6)

Здесь правые части уравнений определяются текущими значениями элементов и проекциями P_i на оси орбитальной системы координат ускорения, вызванного действием возмущающих сил.

Изменения декартовых координат при движении КА в пространственном случае можно описывать уравнениями второго порядка

                    (7)

которые можно переписать в виде системы шести уравнений первого порядка в нормальной форме. Здесь x – декартовы координаты, r – модуль радиус-вектора, U – силовая функция возмущений, m – гравитационный параметр,  – непотенциальные ускорения, вызванные действием возмущающих сил.

Кроме сил гравитационного взаимодействия и светового давления можно учитывать влияние сопротивления атмосферы при движении в окрестности Земли, тягу двигателей на активных участках траектории и другие возмущения.

Направление вектора тяги и моменты относительно основного корпуса КА можно менять при условии, что величина поверхности солнечного паруса и расположение элементов паруса относительно аппарата может изменяться с использованием дополнительных устройств [3; 7; 22]. Тогда можно выбирать управление в процессе маневрирования наилучшим образом.

В случае, когда основными действующими силами можно считать силы гравитационного взаимодействия с Солнцем и световое давление на парус, можно использовать модель фотогравитационного центрального поля для определения перелетов к астероидам или планетам.

Если рассматривается движение в окрестности Земли, то направления двух основных сил не совпадают, но можно в первом приближении полагать, что световой поток определяет постоянную по величине силу, которая проходит коллинеарно прямой, которая проходит через два главных тела системы в рамках ограниченной задачи трех тел [8; 10; 19], а затем учитывать поправки для управления ориентацией благодаря изменениям углового положения или формы паруса. Таким образом в уравнения движения будет входить постоянное возмущение, которое легко учитывать. Особый интерес представляет случай размещения КА в окрестности точек либрации Эйлера-Лагранжа, где малые силы возмущений будут определять характер движения и условия устойчивости.

Список литературы:

1. Егоров В.А. Помазанов М.В. Солнечный парус: принципы конструкции. Управление и перелеты к астероидам. – М.: Препринты ИПМ им. М.В. Келдыша, 1997, 087.
2. Карпасюк И.В., Шмыров А.С. Управление космическим аппаратом с солнечным парусом на низкоширотной околокруговой орбите // Вестник С.-Петерб. ун-та. Сер. 1. 1999. Вып. 4, № 22. – С. 89–93.
3. Королев В.С. Об управлении движением механической системы при переменном распределении массы тел // Известия РАЕН, серия МММИУ, 2000, т. 4. С. 108–117.
4. Королев В.С. Определение движения навигационных спутников с учетом возмущений // Вестн. С-Петерб. ун-та. Серия 10. 2004. Вып. 3–4. С. 39–46.
5. Королев В.С. Задачи оптимального инспектирования астероидов космическим аппаратом // Избранные труды конференции по механике «Шестые Поляховские чтения». – М. 2012. С. 123–126.
6. Королев В.С. Оптимальные траектории перехода космических аппаратов между заданными орбитами различного типа // Технические науки – от теории к практике. 2014, № 32, С. 62–70.
7. Меркулов И.А., Хоромский И.А. Влияние параметров экрана на оценку эффективности солнечного паруса // Труды II чтений, посвященных развитию идей Ф.А. Цандера. – М., 1974, С. 55–63.
8. Новоселов В.С. Аналитическая теория оптимизации в гравитационных полях. – Л.: изд. ЛГУ, 1972, 317 с.
9. Новоселов В.С., Королев В.С. Аналитическая механика управляемой системы. – СПб.: изд. СПбГУ, 2005, 298 с.
10. Новоселов В.С., Королев В.С., Поляхова Е.Н., Шмыров А.С. Аналитические и качественные методы исследования вырожденных случаев, возмущенных и управляемых гамильтоновых систем // Отчет НИР № 96-01-609, РФФИ, 1996.
11. Поляхова Е.Н. Долгопериодические возмущения искусственных спутников под действием светового давления // Вестник Ленингр. Ун-та, 1970, № 7, С. 144–152.
12. Поляхова Е.Н. Определение возмущающих моментов сил давления солнечной радиации, действующей на тело вращения // Труды АО ЛГУ, 1972, № 29, С. 152–163.
13. Поляхова Е.Н. Космический полет с солнечным парусом: проблемы и перспективы. – М.: Наука, 1986. – 304 с.
14. Поляхова Е.Н., Гриневицкая Л.К. Построение приближенного решения уравнений геоцентрического движения космического аппарата с солнечным парусом // Вестник Ленингр. Ун-та, 1973, № 7, С. 134–143.
15. Поляхова Е.Н., Коблик В.В. Солнечный парус – фантастика или реальность космоплавания? – М.: ЛЕНАРД, 2016. – 228 с.
16. Поляхова Е.Н., Королев В.С. Уточнение алгоритма определения моментов прохождения тени для ИСЗ // Труды конференции «Процессы управления и устойчивость». – СПб, СПбГУ, 2004. – С. 192–194.
17. Поляхова Е.Н., Старков В.Н., Степенко Н.А. Полеты космического аппарата с солнечным парусом вне плоскости эклиптики // Материалы III конференции «Устойчивость и процессы управления». – СПб.: СПбУ, 2015. – С. 91–92.
18. Поляхова Е.Н., Шмыров А.С. Физическая модель сил давления световой радиации на плоскость и сферу. Вестник С-Петерб. ун-та. Серия 1. 1994. № 2. – С. 87–104.
19. Поляхова Е.Н., Шмыров А.С., Шмыров В.А. О задаче стабилизации орбитального движения космического аппарата с солнечным парусом в окрестности L1 // Материалы III конференции «Устойчивость и процессы управления». – СПб.: СПбУ, 2015. – С. 149–150.
20. Цандер Ф.А. Об использовании силы давления света для полетов в межпланетном пространстве // «Проблемы полета при помощи реактивных аппаратов. Межпланетные полеты». – М., 1961. – С. 361–381.
21. Forward R.L. Light-Levitated Geostationary Cylindrical Orbits. Journal of the Astronautical Sciences, vol. 29, № 981, Р. 73–80.
22. Forward R.L. Light-Levitated Geostationary Cylindrical Orbits: Correction and Expansion. Journal of the Astronautical Sciences, vol. 38, № 3, 1990, Р. 335–353.
23. Kirpichnikov S.N., Kirpichnikova E.S., Polyakhova E.N., Shmyrov A.S. Planar heliocentric roto-translatory motion of a spacecraft with a solar sail of complex shape // Celestial Mechanics and Dynamical Astronomy, vol. 63, № 3-4, 1996, Р. 255–269.
24. Koblik V.V., Polyakhova E.N., Sokolov L.L., Shmyrov A.S. Controlled solar sailing transfer flights into near-sun orbits under restrictions on sail temperature // Cosmic Research, vol. 34, № 6, 1996, Р. 572–578.
25. Korolev V.S. Problems of spacecraft multi-impulse trajectories modeling // International Conference «Stability and Control Processes», 2015, Р. 91–94.
26. Korolev V.S., Pototskaya I.Yu. Integration of dynamical systems and stability of solution on a part of the variables // Applied Mathematical Sciences, vol. 9 (15), 2015, Р. 721–728.
27. Martyusheva A., Oskina K., Petrov N., Polyakhova   E. Solar radiation pressure influence in motion of asteroids, including near-earth objects // International Conference on Mechanics “Seventh Polyakhov's Reading”, 2015. С. 7106756.
28. Polyakhova E.N., Starkov V.N., Stepenko N.A. Solar sailing out of ecliptic plane // “Stability and Control Processes”, 2015, P. 65–68.