Статья опубликована в рамках: LX Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 25 июля 2016 г.)
Наука: Технические науки
Секция: Машиностроение и машиноведение
Скачать книгу(-и): Сборник статей конференции
дипломов
К МЕТОДИКЕ СОСТАВЛЕНИЯ УРАВНЕНИЯ КИНЕТИЧЕСКОЙ ЭНЕРГИИ РЫЧАЖНОГО РОТОРНОГО МЕХАНИЗМА С ЦЕНТРОБЕЖНЫМ УПРУГИМ ЭЛЕМЕНТОМ
TO THE TECHNIQUE OF DRAWING UP THE EQUATION OF KINETIC ENERGY OF THE LEVER ROTOR MECHANISM WITH THE CENTRIFUGAL ELASTIC ELEMENT
Sayranbek Akhmetov
doctor of Science, professor of Mekhanika department,
Euroasian national university of name L.N. Gumilev,
Kazakhstan, Astana
Nurken Akhmetov
doctor of Science, associate professor, dean of Oil faculty of the
Atyrau instituteof oil and gas,
Kazakhstan, Atyrau
Dana Mukhambetalina
сandidate of Science, associate professor of Mekhanika department, Euroasian national university of name L.N. Gumilev,
Kazakhstan, Astana
Zhamal Isenova
senior teacher of Mekhanika department,
Euroasian national university of name L.N. Gumilev,
Kazakhstan, Astana
АННОТАЦИЯ
Рассмотрен частный случай составления уравнения кинетической энергии рычажного механизма, с центробежным упругим элементом вращающегося вокруг горизонтальной оси. Разработанная обобщающая расчетная схема динамической модели позволяет при составлении уравнении кинетической энергии предусмотреть все возможные случаи сложного движения центробежных элементов, что впоследствии дает возможность исследовать ранее не изученные свойства муфт центробежного типа в качестве механических датчиков в приводах машин.
ABSTRACT
The special case of drawing up the equation of kinetic energy of the lever mechanism with a centrifugal elastic element is considered. The generalizing settlement scheme of dynamic model is developed. The model allows to provide by drawing up the equation of kinetic energy all chances of the difficult movement of her centrifugal elements. It gives subsequently the chance to investigate earlier not studied properties of centrifugal couplings as mechanical sensors in drives of cars.
Ключевые слова: обобщенная динамическая модель, центробежный механизм, кривошип, шатун, упругий ползун, кулиса, двигатель, муфта, рабочая машина, обобщающая координата, обобщающая сила.
Keywords: the generalized dynamic model, the centrifugal mechanism, crank, rod, the elastic ram, the coulisse, the engine, the coupling, the working machine, the generalizing coordinate, the generalizing force.
На основе аналитического обзора литературы разработана обобщенная динамическая модель центробежного механизма, предусматривающая возможность анализировать различные случаи движения и динамической нагруженности, учитывающая особенности работ центробежных муфт на малых оборотах и при больших крутящих моментах при применении их в качестве механических датчиков в приводах технологических машин.
Для того, чтобы учесть такие технические свойства, модель должна быть представлена в виде системы двигатель-муфта-рабочая машина и содержать элементы, как это показано на рис. 1. Центробежный механизм муфты включает в себя вращающийся вокруг горизонтальной оси ведущую и ведомую части. Первая, из которых, представляет собой центробежный сдвоенный кривошипно-шатунный механизм (КШМ) с упругими ползунами 3, которые кинематический связаны с ведомой частью, выполненной в виде дисковой кулисы 4, посредством диаметрально расположенных в ней направляющих пазов 5. Двигатель 1, муфта и рабочая машина 2 расположены соосно. При этом, момент двигателя Мд передается к ведомой части посредством центрального кривошипа 6 и шарнирно связанных с ними шатуном 7 и ползуном 3.
Для работы данной системы в качестве механического датчика нагрузки жесткости упругих элементов (пружин) 8 устанавливаются прямо пропорционально к значению момента сопротивления Мс на валу рабочей машины 2, необходимого для привода его движущих частей в обычном режиме работы.
При превышении Мс установленной (регулируемой) величины усилие кривошипа 6, преодолевая сопротивления упругих элементов 8 передается через шатуны 7 к ползунам 3, перемещая их вдоль направляющих пазов 5 до тех пор, пока не произойдет сцепление с внутренней поверхностью полого шкива (на схеме не показан), посредством которого будет осуществляться обратная кинематическая связь с контролируемым источником нагрузки (например, заслонка, взаимодействующая с дозируемым материалом, или долото, взаимодействующее в горной породой и т. п.).

Рисунок 1. Обобщающая расчетная схема динамической модели рычажного центробежного кривошипно-ползунного механизма
с упругими элементами
В обычном режиме система работает как обычная упругая муфта для передачи момента между валами ведущей и ведомой частей муфты. В этом случае контакт (сцепление) между шкивом и ползунами 3 не произойдет, так как последние, после незначительного перемещения вдоль направляющих пазов 5, занимают в них определенное положение в пределах размеров их длины.
С учетом последующего всестороннего изучения предложенной модели центробежного механизма необходимо построить методику анализа динамики центробежного механизма следующим образом: в начале рассматривается расчетная схема обобщенной динамической модели с учетом масс кривошипа mк, шатуна mш и ползуна mп, и только после этого, на основе полученных результатов обосновываются частные случаи модели.
Сложность нагружения в данной конструктивно-динамической модели центробежного механизма муфты состоит в том, что при вращении КШМ с упругим ползуном вокруг оси, перпендикулярной к вертикальной плоскости, углы между силами тяжестей и инерции звеньев (составных элементов) меняются в зависимости от положения угла поворота (j0+wt) направляющего паза 5 кулисы 4. Кроме того, в некоторых случаях соотношения параметров системы, особенно в переходных режимах пуска и торможения возникает относительное колебательное движение ползуна 3 по направляющему пазу 5, обусловленное появлением силы трения между ними, величина и направление которой колеблются в зависимости от соотношения между кориолисовой силы и силы тяжести ползуна.

Рисунок 2. Расчетная схема центробежного кривошипно-шатунного механизма с упругим ползуном при вращении
их в вертикальной плоскости
В общей постановке задачи, для исследования модели будем рассматривать расчетную схему, показанную на рис. 2. Данная система динамически нагружена с учетом вышеуказанных особенностей ее движения, и она расположена в удобном для анализа в фазовой плоскости положении.
Приводим некоторые особенности составления уравнение движения системы в форме Лагранжа. Для чего отдельно рассматриваем составляющие выводимого уравнения кинетической энергии.
Уравнение движения КШМ в обычном случае характеризуется тем, что кривошип вращается вокруг неподвижной точки, а ползун движется возвратно-поступательно по неподвижной направляющей. В нашем случае, когда, вся система вращается относительно неподвижной точки, и процесс вращения осуществляется посредством подвижного направляющего и связанных с ним КШМ, координаты центров тяжестей его составных элементов, т. е. кривошипа, шатуна и ползуна находятся несколько иначе. Поэтому, в начале проверим возможность выражения массы звеньев через величину плотности, так как это упрощает расчеты переменных координат центров тяжестей звеньев. Для этого вводим некую переменную координату центра масс системы  . Тогда переменные координаты кривошипа, шатуна и ползуна соответственно будут
. Тогда переменные координаты кривошипа, шатуна и ползуна соответственно будут 
В обычном случае кинетическая энергия КШМ выражается следующими зависимостями [4]:
· для кривошипа
 ; (1)
; (1)
· для шатуна
 ; (2)
; (2)
· для ползуна
 ; (3)
; (3)
где: mk, mш, mп – массы кривошипа, шатуна и ползуна соответственно, кг;
rк, rш, кп – обобщенные координаты кривошипа, шатуна и ползуна соответственно, м;
a – угол между кривошипом и направляющей кулисой, град.;
l – безразмерная величина ( l= rк / lш);
lш – длина шатуна, м.
В данном случае движения КШМ, по сравнению с обычным случаем, координаты a, y, r, lш, l оставляем без изменения. Отличающей особенностью будет появление координаты (φ0+ωt), и в связи с этим сложное движение ползуна (вращательное движение вместе с направляющей и поступательное – по направляющей).
Уравнение кинетической энергии можно выразить относительно плотности звеньев. Тогда координаты центра тяжести выражаем через величину  :
:
 (4)
(4)

Элементарная масса кривошипа
 , (5)
, (5)
где: p – плотность материала кривошипа, кг/м3.
Тогда, элементарная кинетическая энергия
,  (6)
(6)
отсюда
 (7)
(7)
Из уравнения (7) видно, что кинетическую энергию любого звена КШМ можно получить путем интегрирования переменной координаты rm по длине звена относительно его плотности. Это показывает целесообразность применения этого способа определения кинетической энергии в сложных случаях движения КШМ (рис. 2).
Учитывая вышеизложенное, получим кинетическую энергию кривошипа в рассматриваемом случае движения:
· координаты 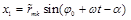 и
и  ,
,
следовательно
,  (8)
(8)
где: φ0 – начальный угол поворота системы;
ω – угловая скорость системы.
Полагая, что координаты центра тяжестей находятся в серединах звеньев, находим координаты центра тяжести шатуна АВ:
 (9)
(9)
 (10)
(10)
Решая (9 и 10) относительно φ0, ω и ψ получим
. 
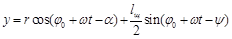 (11)
(11)
Из уравнения (11) можно еще раз легко проверить правильность определения кинетической энергии КШМ в нашем случае. Для этого в уравнении (11) координату ( φ0+ω t) необходимо выразить через π/2, а угол ψ и расстояние lш соответственно через координаты α и λ. Затем, определив их производные, разложив в ряд и отбросив малые параметры можно получить выражение в квадратной скобке уравнения (2) для определения кинетической энергии в обычном случае.
Следует отметить, что разложение в ряд дает точные результаты лишь в том случае если
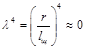 , (12)
, (12)
т. е. если выполняется условие  .
.
Если λ ближе к 1 или λ³ ≥ 1, как например, в нашем случае, то необходимо произвести полный расчет. В нашем случае, полагая, что λ ≥ 1 уравнение (11) можно записать в виде:
 ;
;
 (13)
(13)
Скорость движения шатуна в координатах:
 ;
;
 , (14)
, (14)
где: ψ – угол между шатуном и направляющей кулисой.
Преобразуем координаты в уравнении (14) относительно α :




и полагая что  (15)
(15)
получим:
 (16)
(16)
 (17)
(17)
Кинетическая энергия шатуна АВ определяется по формуле:
 (18)
(18)
где: γ – угол между главным вектором скорости ползуна  и ее составляющей
и ее составляющей  , выражающую скорость относительного движения.
, выражающую скорость относительного движения.
Произведения, выражающие последнее слагаемое в квадратной скобке уравнения (18) преобразуем относительно cos(γ+α) и cos(γ+ψ), затем, выразив cosγ и sinγ через отношение скоростей  , последнее вводим в данное уравнение как переменный безразмерный коэффициент
, последнее вводим в данное уравнение как переменный безразмерный коэффициент  , равный
, равный
 (19)
(19)
Тогда уравнение (18) примет вид
 , (20)
, (20)
Откуда
 (21)
(21)
Координаты центра масс ползуна, т. е. точки В:
 и
и 
Скорость центра масс ползуна в проекциях на ось ОХУ:

 (22)
(22)
Суммарная скорость ползуна:
После необходимого преобразования получим выражение кинетической энергии ползуна
 . (23)
. (23)
Для определения кинетической энергии КШМ необходимо сложить уравнения (8), (20) и (23).
Для определения обобщенных сил, составляем уравнение равновесия моментов относительно опоры О находим реакцию Nt между ползуном и его направляющим:
 .(24)
.(24)
Работа обобщенных сил КШМ в целом вычисляется по формуле:
 (25)
(25)
Работа обобщенных сил элементов КШМ:
· кривошипа
 (26)
(26)
· шатуна
 (27)
(27)
- ползуна
 ; (28)
; (28)
- трения
 (29)
(29)
где: f – коэффициент трения;
sign – знак, показывающий переменность значения слагаемых выражений в квадратной скобке, так как оно меняет свою величину в зависимости от времени;
- упругости пружины
 , (30)
, (30)
где: с – жесткость пружины.
Суммируя работы обобщенных сил и выводя общий множитель за скобку можно определить обобщенную силу КШМ – Qa, затем, ввиду громоздкости и трудоемкости подсчета, выполнив необходимые компьютерные вычисления условия уравнения Лагранжа [3]:
 ,(31)
,(31)
определяем искомое уравнение движения.
Предложенная нами методика вывода уравнения сложной системы движения в виде такой модели (рис. 1), в общей постановке задачи раньше никем не рассматривалась [1; 2]. На основании полученной модели и предложенной общей методики составления можно рассматривать частные случаи движения системы, исключая те или иные элементы, которые обуславливаются в зависимости от цели и задачи прикладного характера. Поэтому, учитывая указанные в начале статьи прикладные стороны цели и задачи исследовании, а также ожидаемое приложение исследуемой динамической модели центробежного механизма муфты, рассматриваем частные случаи движения и нагружения этой системы, обусловленные двумя режимами работы в ней.
Можно выделить два частных случая, соответствующие к двум режимам работы системы:
Случай 1 – когда система, помимо того, как передавать крутящий момент между ведущим и ведомым валами привода машин, одновременно применяется в качестве механического датчика нагрузки, т. е. когда обычная муфта параллельно применяется в качественно новом назначении. Этот случай характеризуется условием
 ; (32)
; (32)
Случай 2 – когда система работает в качестве обычной упругой центробежной муфты для соединения ведущего и ведомого валов и передает между ними крутящий момент в приводе машин. Это характеризуется условием
 (33)
(33)
В первом случае суммарная масса кривошипа mk и шатуна mш превышает массу ползуна mп. Причем, в силу необходимости обеспечения оптимальных соотношении конструкции массы mк и mш ограничиваются обеспечением лишь необходимой и достаточной прочности КШМ муфты. Поэтому сравнительно малой массой ползуна можно пренебречь. Следовательно, сложную систему (рис. 1.) можно представить без учета ползуна в виде замкнутого треугольного контура ОАВ на рис. 2 с переменной координатой центра масс в переходных режимах и постоянной координатой в установившемся режиме. Поскольку, центробежная сила инерции ползуна Фзи кориолисовая сила Фки в данном случае будут отсутствовать, система является мало динамичной и условие (32) будет использоваться в качестве ограничения при расчете и обосновании параметров муфты для работы ее в режиме механического датчика нагрузки. Случай характеризуется малой угловой скоростью валов и большим крутящим моментом.
Во втором случае масса ползуна mш преобладает суммарные массы кривошипа mk и шатуна mш. Особенностью случая характеризуется тем, что имея свойства первого случая, а именно, при средних оборотах вращения и достаточно большом крутящем моменте, в системе возникает кориолисовая сила инерции Фки при относительном движении ползуна вдоль направляющего паза кулисы, а также появляется центробежная сила инерции во всех режимах движения системы. Несомненно, в данном случае система представляет собой динамически сложно нагруженный объект исследования. Поэтому исследование динамики данной системы следует вести на основе рассмотрения условия (33), которое исключает из системы кривошип и шатун. Тогда сложная система (рис. 1) превращается в более упрощенную систему, как это показана на рис. 3.
Интерпретируя условия двух случаев представления динамической системы, на основе разностороннего анализа ее динамики можно разработать методику расчета параметров муфты с упругим центробежным рычажным кривошипно-ползунным механизмом для работы ее в качестве механического датчика нагрузки с учетом случаев (32) и (33).

Рисунок 3. Упрощенная динамическая модель упругого центробежного рычажного кривошипно-ползунного механизма муфты
Список литературы:
1. Ахметов С.М. Обоснование параметров движения ротора с центробежным упругим рычажно-ползунным механизмом / Материалы I Респ. съезда по теорет. и прикл. механике: – Часть 1. – Алматы, 1996. – С. 61–62.
2. Ахметов С.М., Кенжегалиев А.М. Некоторые особенности движения горизонтального ротора с центробежным упругим ползуном // НЖ «Поиск» - научное приложение к международному журналу «Вестник высшей школы Казахстана», 1995, № 5. – С. 117–119.
3. Кожевников С.Н. Динамика машин с упругими звеньями. – Киев: Ан УССР, 1961. – 367 с.
4. Левитский Д.Н. Уравновешивание балансированных станков-качалок. – Проблемы машиностроения и надежности машин, 1995, № 4, – С. 103–106.
дипломов


Оставить комментарий