ИССЛЕДОВАНИЕ однородности искажений частотных коэффициентов ДКП матрицы, вносимых Jpeg-сжатием и медианной фильтрацией цифровых изображений

Статья опубликована в рамках: VIII Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 19 марта 2012 г.)

Наука: Технические науки

Секция: Информатика, вычислительная техника и управление

Скачать книгу(-и): Сборник статей конференции

Библиографическое описание:

Коваленко М.П. ИССЛЕДОВАНИЕ однородности искажений частотных коэффициентов ДКП матрицы, вносимых Jpeg-сжатием и медианной фильтрацией цифровых изображений // Технические науки - от теории к практике: сб. ст. по матер. VIII междунар. науч.-практ. конф. – Новосибирск: СибАК, 2012.

Условия публикаций
Все статьи конференции

Проголосовать за статью

Дипломы участников

У данной статьи нет
дипломов

Статья опубликована в рамках:

Международной заочной научно-практической конференции «ТЕХНИЧЕСКИЕ НАУКИ: ТЕОРЕТИЧЕСКИЕ И ПРИКЛАДНЫЕ АСПЕКТЫ» (Россия, г.Новосибирск, 19 марта 2012г.)

Выходные данные сборника:

«ТЕХНИЧЕСКИЕ НАУКИ: ТЕОРЕТИЧЕСКИЕ И ПРИКЛАДНЫЕ АСПЕКТЫ»: материалы международной заочной научно-практической конференции. (19 марта 2012 г.)

ИССЛЕДОВАНИЕ однородности искажений частотных коэффициентов ДКП матрицы, вносимых Jpeg-сжатием и медианной фильтрацией цифровых изображений

Коваленко Михаил Павлович

аспирант, инженер-программист, МОУ «ИИФ», г. Серпухов

E-mail:

Введение

Стеганографические алгоритмы, производящие встраивание скрываемой информации в частотную область изображений, получили широкое распространение в силу некоторых выгодных отличий от остальных стеганографических алгоритмов. К сильным сторонам данного вида алгоритмов, прежде всего, следует отнести возможность встраивать информацию в изображения-контейнеры, сжатые форматом JPEG, который является одним из наиболее распространенных форматов хранения и передачи мультимедиаконтента на сегодняшний день. Также к преимуществам данного вида алгоритмов можно отнести и достаточно хорошую устойчивость к различного рода внешним воздействиям или атакам на изображение-контейнер.

Частотные свойства матрицы ДКП коэффициентов

В основе большинства стеганографических алгоритмов частотной области лежит дискретно-косинусное преобразование (ДКП). Такие алгоритмы предварительно разбивают исходное изображение-контейнер на блоки, как правило, размером 8×8 пикселей, в дальнейшем подвергающиеся ДКП, результатом которого является матрица коэффициентов, представленная на рисунке 1.

Рисунок 1 – Матрица ДКП коэффициентов

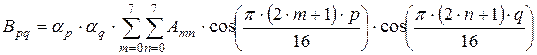, (1)

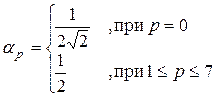и 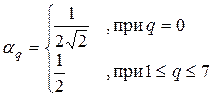, (2-3)

где 0£p£7; 0£q£7; A – матрица, подвергаемая ДКП; B– матрица ДКП коэффициентов.

В ДКП матрице, вычисляемой для блоков размером 8×8 пикселей по формулам 1—3, коэффициенты низкочастотных компонент располагаются ближе к верхнему левому углу, в то время как коэффициенты высокочастотных компонент сгруппированы в правой нижней части матрицы. Низкочастотные коэффициенты содержат преобладающую часть энергии изображения, в то время как высокочастотные компоненты наиболее уязвимы для внешних воздействий [3]. Поэтому авторы большинства алгоритмов считают пригодными для встраивания только среднечастотные коэффициенты. При этом не малую роль играет учет статистических свойств их искажений, вносимых такими преобразованиями цифровых изображений, как, например, Jpeg-сжатие или медианная фильтрация. Исследованию одного из таких свойств, а именно однородности искажений, и посвящена данная работа.

Анализ однородности искажений частотных коэффициентов ДКП матрицы, вносимых Jpeg-сжатием и медианной фильтрацией цифровых изображений

Одним из критериев для проверки однородности двух выборок X₁, X₂, ..., X_m и Y₁, Y₂, ..., Y_n из n и m числовых результатов наблюдений является критерий U-Манна-Уитни [1]. Статистика U Манна-Уитни определяется как число пар (X_i, Y_j) таких, что X_i<Y_j, среди всех m×n пар, и вычисляется по следующей формуле [4]:

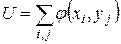, (4)

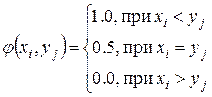. (5)

Ясно, что U может принимать значения от 0 до m×n.

Если объемы выборок больше 20, то распределение U статистики быстро сходится к нормальному [5], имеющему следующие математическое ожидание и среднеквадратическое отклонение [2]:

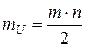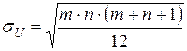, . (6)

В случае же, когда объемы обоих выборок совпадают, будем иметь:

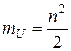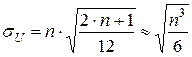, . (7)

Проверим однородность искажений частотных коэффициентов ДКП матрицы, вносимых в цифровые изображения JPEG-сжатием с потерями, выполненным при помощи пакета программ StirMark Benchmark 4.0.129 (JPEG Quality level=90). Используемые для этого изображения представлены на рисунке 2.

Описание: 1063311461 Описание: 1063680841 Описание: 1008652591 Описание: 1008134617

Рисунок 2 – Участвующие в проверке однородности искажений частотных коэффициентов ДКП матрицы изображения

При этом 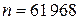, , 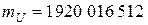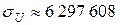. Тогда на уровне значимости 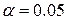значение статистики Uдолжно быть в диапазоне от 1 919 621 609 до 1 920 411 415.

В ходе вычислений, результаты которых представлены в таблице 1, было установлено, что статистически одинаково вели себя коэффициенты 23 и 31, 24 и 35, 25 и 29, 29 и 42, 30 и 31.

Таблица 1

Полученные при JPEG-сжатии значения статистики U

i	j	U_ij	i	j	U_ij	i	j	U_ij
21	22	1901752724	22	29	1926376115	23	37	1916088062
21	23	1905006601	22	30	1925274158	23	38	1915288595
21	24	1904665335	22	31	1924722840	23	39	1918951138
21	25	1906306079	22	32	1930608554	23	40	1918981641
21	26	1898968741	22	33	1919217841	23	41	1918783311

Продолжение Табл.1

i	j	U_ij	i	j	U_ij	i	j	U_ij
21	27	1899076811	22	34	1916959667	23	42	1921479082
21	28	1911020926	22	35	1922437473	24	25	1923571392
21	29	1906503183	22	36	1927685687	24	26	1914898573
21	30	1905101107	22	37	1921166482	24	27	1915882425
21	31	1905336728	22	38	1920459484	24	28	1927833686
21	32	1911575226	22	39	1923908472	24	29	1924165555
21	33	1899648263	22	40	1923962432	24	30	1922879101
21	34	1896958400	22	41	1923682724	24	31	1922629961
21	35	1902428194	22	42	1926635300	24	32	1927499351
21	36	1906972862	23	24	1917627516	24	33	1917903967
21	37	1900403386	23	25	1921609983	24	34	1914925981
21	38	1899040797	23	26	1912458470	24	35	1920278187
21	39	1903331607	23	27	1913889038	24	36	1924836378
21	40	1903509574	23	28	1925864408	24	37	1918639094
21	41	1903165075	23	29	1921785082	24	38	1918349514
21	42	1904962876	23	30	1920432558	24	39	1921369166
22	23	1924459483	23	31	1920146214	24	40	1921497114
22	24	1921208095	23	32	1926201269	24	41	1921863966
22	25	1926061380	23	33	1914720762	24	42	1924269350
22	26	1916076809	23	34	1912017665	25	26	1910966538
22	27	1917990916	23	35	1917601356	25	27	1911903739
22	28	1930353330	23	36	1922855655	25	28	1924138407
25	29	1919855491	26	41	1927853583	28	40	1912853146
25	30	1918510268	26	42	1930587324	28	41	1911821274
25	31	1918347056	27	28	1933627352	28	42	1914800343
25	32	1924663763	27	29	1928642726	29	30	1918951301
25	33	1912642884	27	30	1927545887	29	31	1918476803
25	34	1909885125	27	31	1926912160	29	32	1925651206
25	35	1915590626	27	32	1933443157	29	33	1912323846
25	36	1920874628	27	33	1921289082	29	34	1910113499
25	37	1913998524	27	34	1918801003	29	35	1915860490
25	38	1913076640	27	35	1925285534	29	36	1921530188
25	39	1917068752	27	36	1930018750	29	37	1914446760
25	40	1916906226	27	37	1923291192	29	38	1913562648
25	41	1916632927	27	38	1922411110	29	39	1917361534
25	42	1919272136	27	39	1925462622	29	40	1917555459
26	27	1921337791	27	40	1926034960	29	41	1916750371
26	28	1933966392	27	41	1925799148	29	42	1919950996
26	29	1930069440	27	42	1928768486	30	31	1919633692
26	30	1928728429	28	29	1915423948	30	32	1926639945
26	31	1928196786	28	30	1914323477	30	33	1913378146

Продолжение Табл.1

i	j	U_ij	i	j	U_ij	i	j	U_ij
26	32	1933415667	28	31	1914189830	30	34	1911017520
26	33	1923603227	28	32	1921328431	30	35	1916755685
26	34	1920589588	28	33	1907746736	30	36	1922549030
26	35	1926370726	28	34	1905418200	30	37	1915341429
26	36	1930985430	28	35	1910902841	30	38	1914363281
26	37	1924735851	28	36	1916751387	30	39	1918424625
26	38	1924583373	28	37	1909385548	30	40	1918501300
26	39	1927198581	28	38	1908471508	30	41	1917729925
26	40	1927452381	28	39	1913346133	30	42	1920759654
31	32	1926547960	33	35	1923824388	35	42	1924201037
31	33	1914137882	33	36	1929287309	36	37	1912725187
31	34	1911732437	33	37	1922387811	36	38	1911669818
31	35	1917313818	33	38	1921680890	36	39	1915928969
31	36	1922891122	33	39	1925152675	36	40	1915932312
31	37	1915963359	33	40	1925317192	36	41	1915043176
31	38	1915054409	33	41	1924838573	36	42	1918040311
31	39	1918830630	33	42	1928137355	37	38	1919093014
31	40	1918975903	34	35	1926054265	37	39	1922925259
31	41	1918438077	34	36	1931729343	37	40	1922980068
31	42	1921353342	34	37	1924747247	37	41	1922229836
32	33	1907264857	34	38	1923858790	37	42	1925617794
32	34	1904748696	34	39	1927332609	38	39	1923924962
32	35	1909872480	34	40	1927584271	38	40	1924032335
32	36	1915574176	34	41	1926941928	38	41	1923105244
32	37	1908375450	34	42	1930312134	38	42	1926597706
32	38	1907431669	35	36	1925970717	39	40	1920150528
32	39	1911732611	35	37	1918478687	39	41	1919300420
32	40	1911842472	35	38	1917697660	39	42	1922437350
32	41	1910921064	35	39	1922175160	40	41	1919269234
32	42	1913576648	35	40	1921751150	40	42	1922391196
33	34	1917837557	35	41	1920759050	41	42	1923445286

Итак, только для 5 из 162 пар частотных коэффициентов были получены значения статистики U, которые могут свидетельствовать о статистической схожести поведения. Проверим однородность их искажений, вносимых медианной фильтрацией, выполненной при помощи пакета программ StirMark Benchmark 4.0.129 (размер окна фильтра равен 1).

Таблица 2

Полученные при медианной фильтрации значения статистики U

I	j	U_ij	i	J	U_ij	i	j	U_ij
23	31	461245102	25	29	1915697033	30	31	1918118644
24	35	3407282604	29	42	457820809	—	&‐	—

В ходе указанной проверки, результаты которой представлены в таблице 2, было установлено, что частотные коэффициенты подвержены статистически не однородным искажениям.

Выводы

Частотные коэффициенты ДКП матрицы на уровне значимости 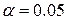подвержены статистически не однородным искажениям.

Список литературы:

1. Борисова Е. В. Формирование и математическая обработка данных в социологии: Учебное пособие. 1-е изд. – Тверь: ТГТУ, 2006. – 120 с.

2. Гайдышев И. Анализ и обработка данных: специальный справочник. – СПб: Питер, 2001. – 752 с.

3. Конахович Г. Ф., Пузыренко А.Ю. Компьютерная стеганография: Теория и практика. – М.: МК-Пресс, 2006. – 283 с.

4. Шитиков В. К., Розенберг Г. С., Зинченко Т. Д. Количественная гидроэкология: методы системной идентификации. – Тольятти: ИЭВБ РАН, 2003. – 463 с.

5. Электронный учебник StatSoft: U критерий Манна-Уитни [электронный ресурс] – Режим доступа. – URL: – www.statsoft.ru/home/portal/ applications/medicine/manna_uitni.htm

Проголосовать за статью

Дипломы участников

У данной статьи нет
дипломов

Оставить комментарий