Статья опубликована в рамках: VIII Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 19 марта 2012 г.)
Наука: Технические науки
Секция: Строительство и архитектура
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
РАСЧЕТ НЕСУЩЕЙ СПОСОБНОСТИ НЕРАЗРЕЗНЫХ ЖЕЛЕЗОБЕТОННЫХ БАЛОК С ИСПОЛЬЗОВАНИЕМ ДЕФОРМАЦИОННОЙ МОДЕЛИ С ЭКСТРЕМАЛЬНЫМ КРИТЕРИЕМ ПРОЧНОСТИ
Шкурупий Александр Анатолиевич
канд. техн. наук, доцент, Полтавский национальный технический университет имени Юрия Кондратюка, г. Полтава, Украина
Е-mail: shbm@ukr.net
Лазарева Елена Николаевна
Аспирант,Полтавский национальный технический университет имени Юрия Кондратюка, г. Полтава, Украина
Постановка проблемы и задачи исследования.Статически неопределимые железобетонные конструкции (ЖБК), в частности неразрезные балки, достаточно широко применяются в различных зданиях и сооружениях как несущие конструкции. Поэтому исследование их работы и совершенствование методики расчета таких конструкций является достаточно важным вопросом в нынешней тенденции развития железобетона.
Применение деформационной модели (ДМ) для расчета прочности и несущей способности ЖБК и их элементов, а также для подбора арматуры в растянутой или сжатой зонах нормального сечения, дает возможность более точно учесть напряженно-деформированное состояние (НДС) на разных стадиях их работы, в том числе и в предельном состоянии. Как отмечено в работах [9, 10], деформационная модель с экстремальным критерием прочности (ДМ с ЭКП) имеет значительные преимущества перед существующими ДМ, которые нуждаются в совершенствовании, особенно для расчета статически неопределимых ЖБК. ДМ с ЭКП является существенно новым подходом для расчета прочности и несущей способности ЖБК и их элементов. Она основана на уравнениях механики деформированного твердого тела (МДТТ) и при учете нисходящей ветви полной диаграммы сжатия (ПДС) бетона, которая отображает процесс снижения несущей способности в результате роста степени его разрушения, и зон упрочнения диаграмм арматурных сталей в сочетании с оптимизационными и численными методами дает возможность аналитически получить характеристики НДС элемента ЖБК в нормальном сечении.
ПолнотаДМ с ЭКП обуславливает необходимость тщательного контроля значений всех предельных параметров НДС элементов ЖБК, в особенности напряжение в растянутой .gif) и сжатой арматуре, поскольку расчетные зависимости существенно отличаются в диапазонах ее упругой и не упругой работы, прежде всего в переармированных конструкциях. Поэтому ограниченный контроль параметров НДС может привести к результатам, которые не отвечают действительности. На основе ДМ с ЭКП и разработанной оптимизационной методики [9, 10] можно решать широкий круг задач при расчете ЖБК (балок, колонн, рам и т. п.). Она дает возможность рассчитывать прочность железобетонных элементов (ЖБЭ) в нормальном сечении при использовании широкого спектра классов прочности бетона на сжатие (
и сжатой арматуре, поскольку расчетные зависимости существенно отличаются в диапазонах ее упругой и не упругой работы, прежде всего в переармированных конструкциях. Поэтому ограниченный контроль параметров НДС может привести к результатам, которые не отвечают действительности. На основе ДМ с ЭКП и разработанной оптимизационной методики [9, 10] можно решать широкий круг задач при расчете ЖБК (балок, колонн, рам и т. п.). Она дает возможность рассчитывать прочность железобетонных элементов (ЖБЭ) в нормальном сечении при использовании широкого спектра классов прочности бетона на сжатие (.gif) ), в том числе и высокопрочных бетонов [8].
), в том числе и высокопрочных бетонов [8].
Исходя из вышеизложенного, проведение теоретических и экспериментальных исследований для изучения работы статически неопределимых ЖБК с учетом перераспределения усилий при образовании в характерных сечениях условных пластических шарниров [7] и определения значений соответствующих им изгибающих моментов, а также предельной нагрузки с использованием метода предельного равновесия [1] является актуальной задачей.
Выделение не решенных ранее частей общей проблемы, которым посвящается статья.Для расчета прочности нормальных сечений ЖБЭ необходимо дополнительное условие. Таким условием может быть условие прочности по бетону
.gif) MACROBUTTON MTPlaceRef \* MERGEFORMAT SEQ MTEqn \h \* MERGEFORMAT ( SEQ MTEqn \c \* Arabic \* MERGEFORMAT 1)
MACROBUTTON MTPlaceRef \* MERGEFORMAT SEQ MTEqn \h \* MERGEFORMAT ( SEQ MTEqn \c \* Arabic \* MERGEFORMAT 1)
и условие прочности по арматуре
.gif) , MACROBUTTON MTPlaceRef \* MERGEFORMAT SEQ MTEqn \h \* MERGEFORMAT ( SEQ MTEqn \c \* Arabic \* MERGEFORMAT 2)
, MACROBUTTON MTPlaceRef \* MERGEFORMAT SEQ MTEqn \h \* MERGEFORMAT ( SEQ MTEqn \c \* Arabic \* MERGEFORMAT 2)
где соответственно .gif) – деформации наиболее сжатого волокна бетона и растянутой арматуры ЖБЭ, которые возникают от внешней нагрузки,
– деформации наиболее сжатого волокна бетона и растянутой арматуры ЖБЭ, которые возникают от внешней нагрузки, .gif) – предельные деформации наиболее сжатого волокна бетона и растянутой арматуры.
– предельные деформации наиболее сжатого волокна бетона и растянутой арматуры.
На сегодняшний день, ни одна из существующих ДМ, кроме ДМ с ЭКП, не дает возможности рассчитывать прочность и несущую способность ЖБК и их элементов, которые работают на различные виды деформирования (изгиб, центральное и внецентренное сжатие или растяжение и т. п.) без наперед заданного значения .gif) [2, 3, 12]. Они нуждаются в данных экспериментальных исследований, в том числе и экспериментальном определении
[2, 3, 12]. Они нуждаются в данных экспериментальных исследований, в том числе и экспериментальном определении .gif) . В действительности,
. В действительности, .gif) является критериальной характеристикой, которая зависит от многих факторов, основными из которых являются: класс прочности бетона на сжатие, форма поперечного сечения, класс арматурной стали и ее расположение по сечению. Только ДМ с ЭКП дает возможность аналитически получить величину
является критериальной характеристикой, которая зависит от многих факторов, основными из которых являются: класс прочности бетона на сжатие, форма поперечного сечения, класс арматурной стали и ее расположение по сечению. Только ДМ с ЭКП дает возможность аналитически получить величину .gif) в результате расчета с использованием методики приведенной в работах [9, 10].
в результате расчета с использованием методики приведенной в работах [9, 10].
Целью работы является расчет прочности и несущей способности неразрезных железобетонных балок с использованием ДМ с ЭКП из бетонов разной прочности на сжатие, армированных стержневой арматурой, загруженных сосредоточенными силами в пролетах и сравнение результатов расчетов с экспериментальными данными, приведенными в работах [4, 5, 6].
Изложение основного материала. Теоретические исследования ограничивались задачей расчета прочности и несущей способности железобетонных неразрезных балок с применением ДМ с ЭКП, оптимизационных и численных методов [10], а также метода предельного равновесия [1].
Расчетные положения приведены в работе [9]. Состояние разрушения нормального сечения описывается расчетными схемами усилий и деформаций, которые приведены на рисунке 1.

Рис. 1 – Расчетные схемы для расчета прочности нормального сечения ЖБЭ
Расчетные зависимости:
- Физические:
а) для бетона – ПДС представлена в виде аппроксимации рекомендованной в нормах [2, 12] (рис. 2, а)
 MACROBUTTON MTPlaceRef \* MERGEFORMAT SEQ MTEqn \h \* MERGEFORMAT ( SEQ MTEqn \c \* Arabic \* MERGEFORMAT 3)
MACROBUTTON MTPlaceRef \* MERGEFORMAT SEQ MTEqn \h \* MERGEFORMAT ( SEQ MTEqn \c \* Arabic \* MERGEFORMAT 3)
где уровень деформации  и параметр деформативно-прочностныхсвойств бетона
и параметр деформативно-прочностныхсвойств бетона 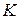 определяются по формулам
определяются по формулам
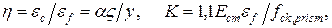 MACROBUTTON MTPlaceRef \* MERGEFORMAT SEQ MTEqn \h \* MERGEFORMAT ( SEQ MTEqn \c \* Arabic \* MERGEFORMAT 4)
MACROBUTTON MTPlaceRef \* MERGEFORMAT SEQ MTEqn \h \* MERGEFORMAT ( SEQ MTEqn \c \* Arabic \* MERGEFORMAT 4)
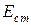 – начальный модуль упругости бетона (
– начальный модуль упругости бетона ( );
);
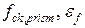 – напряжение и деформация в максимуме кривой
– напряжение и деформация в максимуме кривой 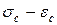 (рис. 2, а)
(рис. 2, а)
 .
.
Аналитические выражения для 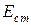 и
и .gif) приведенные в работе [8].
приведенные в работе [8].
Деформация .gif) определяется по формуле
определяется по формуле
.gif) MACROBUTTON MTPlaceRef \* MERGEFORMAT SEQ MTEqn \h \* MERGEFORMAT ( SEQ MTEqn \c \* Arabic \* MERGEFORMAT 5)
MACROBUTTON MTPlaceRef \* MERGEFORMAT SEQ MTEqn \h \* MERGEFORMAT ( SEQ MTEqn \c \* Arabic \* MERGEFORMAT 5)
б) для арматуры аналитические выражения диаграммы растяжения (сжатию) разделены на два известных типа: с физическим пределом текучести .gif) и с условным пределом текучести
и с условным пределом текучести 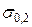 (рис. 3). На интервале ВС (рис. 3 а)
(рис. 3). На интервале ВС (рис. 3 а) 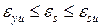 зона упрочнения аппроксимируется параболой
зона упрочнения аппроксимируется параболой
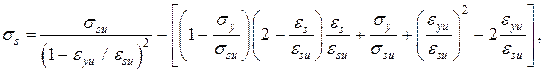 MACROBUTTON MTPlaceRef \* MERGEFORMAT SEQ MTEqn \h \* MERGEFORMAT ( SEQ MTEqn \c \* Arabic \* MERGEFORMAT 6)
MACROBUTTON MTPlaceRef \* MERGEFORMAT SEQ MTEqn \h \* MERGEFORMAT ( SEQ MTEqn \c \* Arabic \* MERGEFORMAT 6)
где 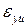 – деформация в конце площадки текучести (точка В)
– деформация в конце площадки текучести (точка В)  – напряжение (предел прочности) и деформация в точке максимума С диаграммы
– напряжение (предел прочности) и деформация в точке максимума С диаграммы 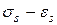 (рис. 3, а).
(рис. 3, а).
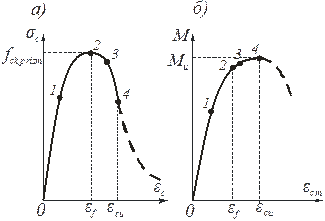
Рис. 2 – Допредельные (1,2,3) и предельное (4) состояния на диаграмме сжатия бетона (а) и кривой «момент в сечении – деформация сжатой грани бетона» (б)
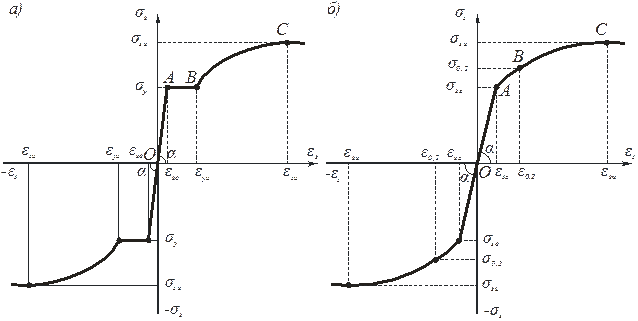
Рис. 3 – Диаграммы растяжения (сжатия) арматурных сталей с физическим (а) и условным (б) пределом текучести
Для арматуры с условным пределом текучести применяется линейно-двупараболическая аппроксимация диаграммы растяжения (сжатия) [10]
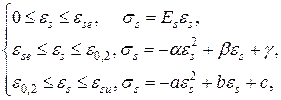 MACROBUTTON MTPlaceRef \* MERGEFORMAT SEQ MTEqn \h \* MERGEFORMAT ( SEQ MTEqn \c \* Arabic \* MERGEFORMAT 7)
MACROBUTTON MTPlaceRef \* MERGEFORMAT SEQ MTEqn \h \* MERGEFORMAT ( SEQ MTEqn \c \* Arabic \* MERGEFORMAT 7)
в которой
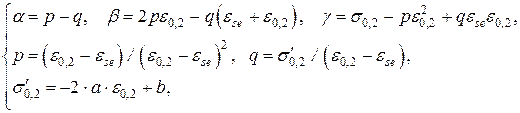 MACROBUTTON MTPlaceRef \* MERGEFORMAT SEQ MTEqn \h \* MERGEFORMAT ( SEQ MTEqn \c \* Arabic \* MERGEFORMAT 8)
MACROBUTTON MTPlaceRef \* MERGEFORMAT SEQ MTEqn \h \* MERGEFORMAT ( SEQ MTEqn \c \* Arabic \* MERGEFORMAT 8)
 MACROBUTTON MTPlaceRef \* MERGEFORMAT SEQ MTEqn \h \* MERGEFORMAT ( SEQ MTEqn \c \* Arabic \* MERGEFORMAT 9)
MACROBUTTON MTPlaceRef \* MERGEFORMAT SEQ MTEqn \h \* MERGEFORMAT ( SEQ MTEqn \c \* Arabic \* MERGEFORMAT 9)
где исходными параметрами арматуры являются: модуль упругости  , предел пропорциональности
, предел пропорциональности 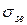 , условный предел текучести
, условный предел текучести 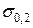 , предел прочности
, предел прочности 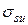 и соответствующие им деформации –
и соответствующие им деформации – 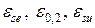 .
.
- Геометрические.Зависимости определялись с использованием гипотезы плоских сечений, что позволяет выразить через деформацию
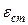 деформации сжатой зоны бетона
деформации сжатой зоны бетона 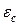 на уровне волокон с координатой
на уровне волокон с координатой 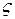 а также деформации растянутой и сжатой арматуры (рис. 1):
а также деформации растянутой и сжатой арматуры (рис. 1):
 ; MACROBUTTON MTPlaceRef \* MERGEFORMAT SEQ MTEqn \h \* MERGEFORMAT ( SEQ MTEqn \c \* Arabic \* MERGEFORMAT 10)
; MACROBUTTON MTPlaceRef \* MERGEFORMAT SEQ MTEqn \h \* MERGEFORMAT ( SEQ MTEqn \c \* Arabic \* MERGEFORMAT 10)
 ; MACROBUTTON MTPlaceRef \* MERGEFORMAT SEQ MTEqn \h \* MERGEFORMAT ( SEQ MTEqn \c \* Arabic \* MERGEFORMAT 11)
; MACROBUTTON MTPlaceRef \* MERGEFORMAT SEQ MTEqn \h \* MERGEFORMAT ( SEQ MTEqn \c \* Arabic \* MERGEFORMAT 11)
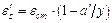 , MACROBUTTON MTPlaceRef \* MERGEFORMAT SEQ MTEqn \h \* MERGEFORMAT ( SEQ MTEqn \c \* Arabic \* MERGEFORMAT 12)
, MACROBUTTON MTPlaceRef \* MERGEFORMAT SEQ MTEqn \h \* MERGEFORMAT ( SEQ MTEqn \c \* Arabic \* MERGEFORMAT 12)
где 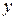 – высота сжатой зоны бетона,
– высота сжатой зоны бетона, 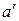 – расстояние от равнодействующей в арматуре сжатой зоны бетона до ближайшей грани сечения,
– расстояние от равнодействующей в арматуре сжатой зоны бетона до ближайшей грани сечения, 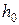 – рабочая высота сечения. Приняв обозначение
– рабочая высота сечения. Приняв обозначение 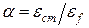 , получим, что
, получим, что  , где
, где 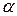 – относительная деформация сжатой грани бетона ЖБЭ в нормальном сечении.
– относительная деформация сжатой грани бетона ЖБЭ в нормальном сечении.
- Уравнения равновесия.
 , MACROBUTTON MTPlaceRef \* MERGEFORMAT SEQ MTEqn \h \* MERGEFORMAT ( SEQ MTEqn \c \* Arabic \* MERGEFORMAT 13)
, MACROBUTTON MTPlaceRef \* MERGEFORMAT SEQ MTEqn \h \* MERGEFORMAT ( SEQ MTEqn \c \* Arabic \* MERGEFORMAT 13)
 . MACROBUTTON MTPlaceRef \* MERGEFORMAT SEQ MTEqn \h \* MERGEFORMAT ( SEQ MTEqn \c \* Arabic \* MERGEFORMAT 14)
. MACROBUTTON MTPlaceRef \* MERGEFORMAT SEQ MTEqn \h \* MERGEFORMAT ( SEQ MTEqn \c \* Arabic \* MERGEFORMAT 14)
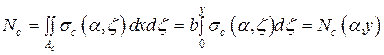 , MACROBUTTON MTPlaceRef \* MERGEFORMAT SEQ MTEqn \h \* MERGEFORMAT ( SEQ MTEqn \c \* Arabic \* MERGEFORMAT 15)
, MACROBUTTON MTPlaceRef \* MERGEFORMAT SEQ MTEqn \h \* MERGEFORMAT ( SEQ MTEqn \c \* Arabic \* MERGEFORMAT 15)
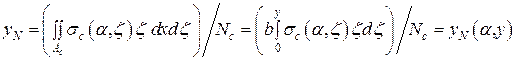 MACROBUTTON MTPlaceRef \* MERGEFORMAT SEQ MTEqn \h \* MERGEFORMAT ( SEQ MTEqn \c \* Arabic \* MERGEFORMAT 16)
MACROBUTTON MTPlaceRef \* MERGEFORMAT SEQ MTEqn \h \* MERGEFORMAT ( SEQ MTEqn \c \* Arabic \* MERGEFORMAT 16)
Используя зависимости (3)-(14), с учетом (15) и (16) получим систему уравнений с неизвестными 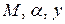 . Для определения неизвестных используем (13), (14) и дополнительное условие (17) в виде ЭКП нормального сечения элемента ЖБК (рис. 2, б)
. Для определения неизвестных используем (13), (14) и дополнительное условие (17) в виде ЭКП нормального сечения элемента ЖБК (рис. 2, б)
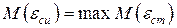 . MACROBUTTON MTPlaceRef \* MERGEFORMAT SEQ MTEqn \h \* MERGEFORMAT ( SEQ MTEqn \c \* Arabic \* MERGEFORMAT 17)
. MACROBUTTON MTPlaceRef \* MERGEFORMAT SEQ MTEqn \h \* MERGEFORMAT ( SEQ MTEqn \c \* Arabic \* MERGEFORMAT 17)
В результате получим оптимизационную задачу нелинейного математического программирования на условный экстремум с целевой функцией (17) при ограничениях-равенствах (13), (14) которая решается с использованием ПЭВМ по специально разработанной авторами прикладной программе в OS Windows.
Теоретические расчеты прочности железобетонных неразрезных балок сравнивались с экспериментальными данными исследований [4, 5, 6], которые проводились на балках с соотношением длины пролета 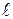 к высоте сечения
к высоте сечения  больше 10. Сечения балки имели прямоугольную форму с постоянными геометрическими размерами по всей длине. Данное условие дает возможность пренебрегать влиянием поперечных сил при расчете прочности и несущей способности балки. Шаг хомутов принимался таким образом, что балки разрушались по нормальными сечениям.
больше 10. Сечения балки имели прямоугольную форму с постоянными геометрическими размерами по всей длине. Данное условие дает возможность пренебрегать влиянием поперечных сил при расчете прочности и несущей способности балки. Шаг хомутов принимался таким образом, что балки разрушались по нормальными сечениям.
В работах [4, 5] использовались балки с 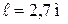 в качестве продольной арматуры использовались высокопрочные арматурные стержни класса А-IV, марки 80С с условным пределом текучести.
в качестве продольной арматуры использовались высокопрочные арматурные стержни класса А-IV, марки 80С с условным пределом текучести.
В работе [6] балки имели пролеты по 3 м с размерами поперечного сечения 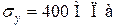 . В качестве продольной арматуры использовались арматурные стержни класса А-III (марки 35ГС) с минимальным значением предела текучести. Призменная прочность бетона для железобетонных неразрезных балок этой серии составляла
. В качестве продольной арматуры использовались арматурные стержни класса А-III (марки 35ГС) с минимальным значением предела текучести. Призменная прочность бетона для железобетонных неразрезных балок этой серии составляла 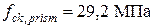 а начальный модуль упругости –
а начальный модуль упругости – 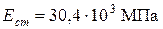 .
.
Расчетная схема неразрезных балок [4, 5, 6] изображена на рисунке 4, где  – интенсивность равномерно распределенной нагрузки от собственного веса конструкции,
– интенсивность равномерно распределенной нагрузки от собственного веса конструкции, 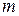 – коэффициент соотношения между сосредоточеннымисилами.
– коэффициент соотношения между сосредоточеннымисилами.

Рис. 4 Расчетная схема балки
Для сравнения теоретических расчетов несущей способности неразрезных балок, полученных по предлагаемой методике с использованием метода предельного равновесия [1], с экспериментальными данными, использовались те же физико-механические характеристики материалов, геометрические размеры, характер армирования сечений, которые приведены в работах [4, 5, 6]. Размещение расчетных сечений неразрезных балок и измерительных приборов, а также характер их армирования показано на рисунке 5.
В экспериментальных образцах приведенных в публикациях [4, 5] .gif) . В работе [6] для балок разных серий
. В работе [6] для балок разных серий 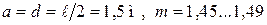 . Значения предельных изгибающих моментов в пролетах и на опоре (рис. 6) вычислены по методике ДМ с ЭКП с использованием специально разработанной авторами прикладной программы для ПЭВМ. Учитывая схему расположения нагрузки и исходя из равенства балочных моментов, значения теоретических предельных нагрузок определяли из зависимости
. Значения предельных изгибающих моментов в пролетах и на опоре (рис. 6) вычислены по методике ДМ с ЭКП с использованием специально разработанной авторами прикладной программы для ПЭВМ. Учитывая схему расположения нагрузки и исходя из равенства балочных моментов, значения теоретических предельных нагрузок определяли из зависимости
 . MACROBUTTON MTPlaceRef \* MERGEFORMAT SEQ MTEqn \h \* MERGEFORMAT ( SEQ MTEqn \c \* Arabic \* MERGEFORMAT 18)
. MACROBUTTON MTPlaceRef \* MERGEFORMAT SEQ MTEqn \h \* MERGEFORMAT ( SEQ MTEqn \c \* Arabic \* MERGEFORMAT 18)
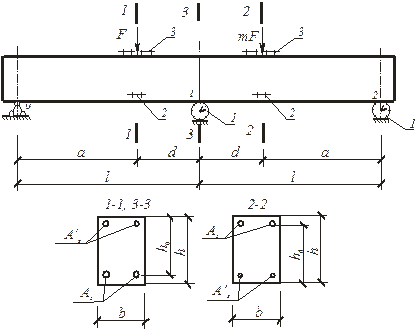
Рис. 5. Характер армирования и схема расположения измерительных приборов и расчетных сечений балок: 1 – кольцевой динамометр; 2–тензометр для арматуры (база 100 мм); 3 – тензометр для бетона (база 100 мм)
Используя метод предельного равновесия [1], получим предельные значения сосредоточенных сил в пролетах балки. Их величины в сравненнии с данными экспериментов опубликованных в работах [4, 5, 6] приведены в таблицах 1 и 2.
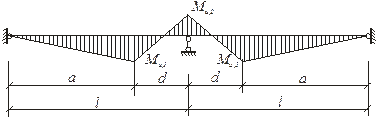
Рис. 6. Эпюра изгибающих моментов балки в предельном состоянии
По результатам расчетов, величины предельных изгибающих моментов в сечениях 1 и 2 для балок обеих серий (Б-4 и Б-5) [6] равняются соответственно 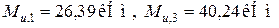 . Расчетные значения предельных изгибающих моментов на опоре 1 (сечение 3) разные, потому что в этом сечении различное продольное армирование балок серий Б-4 и Б-5. Их значения равняются
. Расчетные значения предельных изгибающих моментов на опоре 1 (сечение 3) разные, потому что в этом сечении различное продольное армирование балок серий Б-4 и Б-5. Их значения равняются 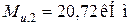 (Б-4) и
(Б-4) и 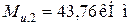 (Б-5).
(Б-5).
Таблица 1
Сопоставление теоретических и экспериментальных значений предельных нагрузок по данным приведенным в работе [6]
|
Серия экспериментальных балок [1] |
Экспериментальные значения предельной нагрузки, кН |
Расчетные значения предельной нагрузки, кН |
|
|
||
|
|
|
|
||||
|
Б-4 |
46,87 |
68,14 |
49,00 |
67,47 |
0,96 |
1,01 |
|
Б-5 |
66,37 |
98,60 |
64,36 |
82,83 |
1,03 |
1,19 |
|
Средняя относительная погрешность, % |
4,70 |
|||||
Таблица 2
Сопоставление экспериментальных и теоретических значений предельных изгибающих моментов и нагрузок по данным приведенным в работах [4, 5]
|
№ серии |
Шифр образца |
Опорный |
|
Пролетный |
|
|
|
|
||
|
|
|
|
|
|||||||
|
кНм |
кНм |
кН |
||||||||
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
|
I |
БОИ-1А |
47,1 |
36,74 |
1,28 |
34,6 |
36,42 |
0,95 |
110,5 |
101,7 |
1,09 |
|
БОИ-1Б |
42,8 |
36,11 |
1,19 |
38,7 |
37,88 |
1,02 |
112 |
103,5 |
1,08 |
|
|
БОИ-2А |
41,1 |
32,02 |
1,28 |
31,5 |
31,53 |
1,00 |
100 |
88,31 |
1,13 |
|
|
БОИ-2Б |
40,6 |
31,6 |
1,28 |
34,5 |
33,21 |
1,04 |
103,1 |
90,63 |
1,14 |
|
|
II |
БВИ-3А |
59 |
51,08 |
1,15 |
51 |
51,64 |
0,99 |
150,6 |
143,1 |
1,05 |
|
БВИ-3Б |
60,3 |
51,28 |
1,18 |
49 |
52,4 |
0,94 |
148,7 |
144,6 |
1,03 |
|
|
БВИ-4А |
35,4 |
30,56 |
1,16 |
30,9 |
30,96 |
1,00 |
93,7 |
85,73 |
1,09 |
|
|
БВИ-4Б |
33 |
30,64 |
1,08 |
29,3 |
32,19 |
0,91 |
88,3 |
87,86 |
1,00 |
|
|
III |
БВУ-5А |
54,5 |
44,14 |
1,23 |
41 |
46,02 |
0,89 |
136 |
126 |
1,08 |
|
Среднеарифметическое значение |
1,08 |
|||||||||
|
Среднеквадратичное отклонение |
0,039 |
|||||||||
|
Коэффициент вариации, % |
3,63 |
|||||||||
|
Коэффициент асимметрии |
– 0,13 |
|||||||||
|
Коэффициент эксцесса |
– 0,46 |
|||||||||
Выводы
- ДМ с ЭКП основывается на уравнениях МДТТ (статических, геометрических, физических), учитывает реальные диаграммы работы материалов и в сочетании с ЭКП дает возможность решать практические инженерные задачи.
- Такой подход в совокупности с численными и оптимизационными методами, позволяет анализировать полный комплекс предельных параметров нормальных сечений в стадии разрушения, дает возможность определить предельные значение изгибающих моментов в сечениях, в которых образуются условные пластические шарниры и с использованием метода предельного равновесия учитывать перераспределение усилий в статически неопределимых системах и определять предельные нагрузки.
- Статистический анализ сравнения теоретических и экспериментальных данных расчета прочности и несущей способности неразрезных железобетонных балок, которые приведены в таблицах 1 и 2 свидетельствуют о хорошей сходимости соотношений расчетных значений предельных нагрузок с экспериментальными.
Список литературы:
- Гвоздев А. А. Расчёт несущей способности конструкций по методу предельного равновесия. Сущностьметодаиегообоснование– М.: Госстройиздат, 1949. – 280 с.
- ДБН В.2.6-98:2009. Бетоннітазалізобетонніконструкції– К.: МінрегіонбудУкраїни, 2011. – 72 с.
- ДСТУ Б В.2.6-156: 2010. Конструкціїбудинківіспоруд. Бетоннітазалізобетонніконструкціїзважкогобетону– К.: МінрегіонбудУкраїни, 2010. – 168 с.
- Крылов С. М., Гуща Ю. П., Абаканов М.С. Несущая способность статически неопределимых железобетонных балок из бетонов прочностью до 90 МПа, армированных высокопрочной стержневой арматурой // Поведение бетонов и элементов железобетонных конструкций при воздействии различной длительности. Под ред. А. А. Гвоздева, С. М. Крылова – М.: НИИЖБ, 1980. – С. 102—119.
- Крылов С. М., Гуща Ю. П., Абаканов М. С. Перераспределение усилий в статически неопределимых железобетонных конструкциях, армированных сталями без площадки текучести // Прочность, жесткость и трещиностойкость железобетонных конструкций. – М.: НИИЖБ, 1979. – С. 171—186.
- Оатул А. А., Чирков В. П. Исследование естественного распределения усилий в неразрезных железобетонных балках с ненапрягаемой арматурой при длительном действии эксплуатационной нагрузки // Исследования по бетону и железобетону. Сборник трудов № 34 Челябинского политехнического института. – Челябинск: ЧОТУП, 1965. – С. 116—135.
- Тихий М., Ракосник Й. Расчёт железобетонных конструкций в пластической стадии. // Перераспределение усилий; пер. с чешск. – М.: Стройиздат, 1976. – 198 с.
- Шкурупій О. А, Бабич Є. М. Аналітичне визначення фізико-механічних характеристик бетону // Ресурсоекономні матеріали, конструкції, будівлі та споруди: Збірник наукових праць. – Рівне: НУВГП, 2011. – Вип. 21. – С. 401—407.
- Шкурупій О. А. Міцність залізобетонних конструкцій та їх елементів на основі деформаційної моделі з екстремальним критерієм // Будівельні конструкції: Міжвідомчий науково-технічний збірник наукових праць (будівництво). – Вып. 74: В 2-х кн.: Книга 1. – Київ, ДП НДІБК, 2011. – С. 605—614.
- Шкурупій О. А., Лазарєв Д. М. Використання чисельних і оптимізаційних методів для розрахунку міцності нормальних перерізів залізобетонних елементів на основі деформаційної моделі з екстремальним критерієм // Коммунальное хозяйство городов: сб. науч. тр. – Вып. 76. – К.: Техника, 2007. – С. 71—79.
- Шкурупій О.А., Лазарєва О.М. Розрахунок міцності статично невизначуваних залізобетонних конструкцій // Ресурсоекономні матеріали, конструкції, будівлі та споруди: збірник наукових праць – Рівне: НУВГП, 2011 – Вип.22. – С. 518—525.
- Eurocode 2: Design of Concrete Structures. EN 1992 – 1.1: General Rules and Rules for buildings. – Brussels: CEN, 2004.–226 p.
дипломов


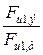

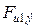

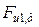


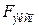

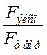

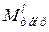
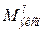
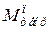
Оставить комментарий