МОДЕЛИРОВАНИЕ  ДИЭЛЕКТРИЧЕСКИХ  ЦИЛИНДРОВ  ДИФРАКЦИОННЫМ  МЕТОДОМ

Андросик  Андрей  Борисович

канд.  техн.  наук,  доцент  МГОУ,  г.  Москва

Воробьев  Сергей  Андреевич

канд.  техн.  наук,  профессор  МГОУ,  г.  Москва

Мировицкая  Светлана  Дмитриевна

канд.  техн.  наук,  доцент  МГОУ,  г.  Москва

E-mail: 

DIFFRACTION  METHOD  OF  MODELING  DIELECTRIC  CYLINDERS

Andrey  Androsik

Candidate  of  Technical  Sciences,  Associate  Professor  of  MSOU,  Moscow

Sergei  Vorobev

Candidate  of  Technical  Sciences,  Professor  of  MSOU,  Moscow

Svetlana  Mirovitskaya

Candidate  of  Technical  Sciences,  Associate  Professor  of  MSOU,  Moscow

Аннотация

Рассмотрены  особенности  расчета  картин  дифракции  на  диэлектрических  цилиндрах  различных  типов.

Abstract

The  peculiarities  of  calculation  of  pictures  of  diffraction  on  a  dielectric  cylinders  of  various  types  are  considered.

Ключевые  слова:  дифракция;  моделирование;  диэлектрический  цилиндр.

Keywords:  diffraction;  simulation;  dielectric  cylinder

Работа  посвящена  анализу  основ  теории  дифракции  плоских  волн  на  диэлектрических  цилиндрах,  на  основе  которого  создан  модифицированный  метод  [1,  с.  43,  2,  с.  124,  3,  с.  209].  Решение  задачи  дифракции  плоской  волны  на  круговом  металлическом  и  однородном  диэлектрическом  цилиндре  записывается  в  виде  разложения  по  цилиндрическим  функциям,  как  для  параллельной,  так  и  перпендикулярной  поляризации  волн  относительно  оси  цилиндра.  Базовой  моделью  является  однородный  цилиндр  без  оболочки  с  радиусом  R₁  и  показателем  преломления  диэлектрика  n₁,  на  который  падает  монохроматическая  волна  длиной  λ,  распространяющаяся  в  окружающем  пространстве  с  показателем  преломления  n₀.  Сформированная  картина  дифракции  наблюдается  в  дальней  зоне.  Интенсивность  излучения  I(a),  рассеянного  в  направлении  азимутального  угла  α  в  дальней  зоне  на  расстоянии  r  от  оси  металлического  цилиндра  много  большем,  чем  его  диаметр  ()  описывается  формулой

,

которая  получена  из  точного  решения  уравнений  Максвелла  с  соответствующими  граничными  условиями.  Для  случая  диэлектрического  цилиндра  поле  представляется  в  виде  двух  частных  решений  для  обеих  геометрических  зон:  вне  световода  и  внутри  него,  учитывающих  поляризацию  падающего  излучения

.

При  нормальном  падении  излучения  коэффициенты  в  выражениях  для  рассеянного  поля  имеют  вид:  поле  параллельно  XZ

,

поле  параллельно  YZ

.

Дифракционная  картина  для  диэлектрического  цилиндра  с  R₁=200  мкм  и  n₁=1,5818,  построенная  с  точностью  600  точек/градус  в  диапазоне  углов  a  =0-0,3  представлена  на  рис.  1.

В  случае  полого  диэлектрического  цилиндра  с  большим  наружным  диаметром  регулярный  участок  картины  рассеяния  незначителен  (α  ≈  0  –  0,25)  при  2R_{1  =}  1400  мкм,  2R₂  =  700  мкм,  и  n₁  =  1,6,  n₂  =  1,0  (рис.  2).  С  увеличением  угла  α  регулярность  пропадает,  а  перепады  интенсивности  увеличиваются.

Поведения  картин  принципиально  различно,  что  свидетельствует  о  весьма  высокой  зависимости  дифракционных  диаграмм  от  изменения  параметров  диэлектрического  цилиндра,  а,  следовательно,  чувствительности  дифракционного  метода  измерений  цилиндров. 

Особенности  явления  рассеяния  волн  диэлектрическим  цилиндром  при  облучении  его  двумя  плоскими  волнами,  распространяющимися  под  различными  углами.  Целесообразно  осуществлять  исследование  формы  поперечного  сечения  цилиндров  путем  зондирования  его  двумя  облучающими  пучками.  Рассмотрим  падение  на  цилиндр  перпендикулярно  оси  двух  синфазных  плоских  Е  —  поляризованных  волны  равной  амплитуды.  Направление  распространения  первой  плоской  волны  составляет  с  осью  0Х  азимутальный  угол  θ,  а  второй  волны  —  угол  (-θ).  Итак,  угол  между  направлениями  распространения  двух  волн  составляет  (2θ).  Диаграмма  рассеяния  (асимптотическое  поведение  рассеянного  суммарного  поля  в  дальней  зоне  при  большом  удалении  от  цилиндра)  представима  в  виде:

где: 

С  —  коэффициент,  зависящий  от  интенсивности  падающего  излучения,  угол  j  отсчитывается  от  положительного  направления  оси  ОХ.  Коэффициенты  b_m  для  двухслойного  цилиндра  с  радиусом  сердцевины  и  оболочки  R₂  и  R₁  и  показателями  преломления  сердцевины  и  оболочки  n₂  и  n₁  вычисляются  по  формулам 

,    .

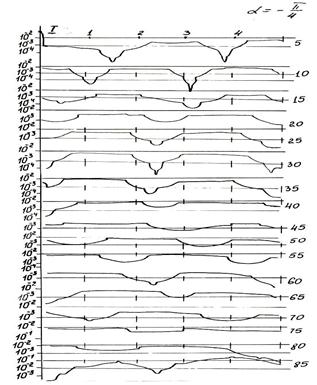
Модельные  исследования  облучения  двухслойных  диэлектрических  цилиндров  двумя  волнами  иллюстрируются  серией  кривых  рис.  3,  а-е  при  R₁  =  20  мкм,  R₂  =  15  мкм,  n₁  =  1,3  ,  n₂  =  1,6  с  точностью  вычисления  75  точек/градус  при  различных  углах  между  облучающими  пучками.

Анализ  кривых  показывает,  что  когда  угол  между  лучами  мал,  наблюдается  расширение  центрального  максимума.  Поведение  дифракционных  диаграмм  резко  меняется  при  добавлении  к  углу  α=  π/4  малых  величин:  Δα=π/100  и  Δα=π/200  (рис.  3,  в,  г).

При  анализе  случая  облучения  двухслойного  цилиндра  двумя  плоскими  волнами  установлено  следующее:  если  сердцевина  цилиндра  симметрична,  то  и  диаграмма  рассеяния  также  симметрична.  Если  же  форма  сердцевины  изменяется,  то  симметрия  диаграммы  пропадает.  Этим  предложенным  методом  легко  установить  концентричность  сердцевины  и  оболочки  прозрачного  диэлектрического  цилиндра.

Список  литературы:

1.Андросик  А.Б.,  Воробьев  С.А.,  Мировицкая  С.Д.  Волноводная  и  интегральная  фотоника.  М.:  МГОУ,  2011.  —  370  с.

2.Воробьев  С.А.,  Андросик  А.Б.,  Мировицкая  С.Д.  Вычислительная  фотоника.  Основы,  задачи,  методы  анализа.  —  Lambert  Academic  Publishing  —  2012  —  183  c.

3.Лазарев  Л.П.,  Мировицкая  С.Д.  Контроль  геометрических  и  оптических  параметров  волокон.  М.:  Радио  и  связь,  1988.  —  280  с.