Статья опубликована в рамках: XLI Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 24 декабря 2014 г.)
Наука: Технические науки
Секция: Информатика, вычислительная техника и управление
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
СИНТЕЗ ПРОГНОЗИРУЮЩЕЙ МОДЕЛИ ПО ЭКСПЕРЕМЕНТАЛЬНЫМ ДАННЫМ
Змеу Константин Виталиевич
канд. техн. наук, заведующий кафедрой Технологий промышленного производства Дальневосточного федерального университета, РФ, г. Владивосток
E -mail: k.zmeu@ieee.org
Ноткин Борис Сергеевич
канд. техн. наук, доцент кафедры Технологий промышленного производства Дальневосточного федерального университета, научный сотрудник Института автоматики и процессов управления ДВО РАН, РФ, г. Владивосток
Онча Юлия Густавовна
аспирант кафедры Технологий промышленного производства Дальневосточного федерального университета, РФ, г. Владивосток
SYNTHESIS OF A PREDICTIVE MODEL ON THE BASIS OF EXPERIMENTAL DATA
Konstantin Zmeu
candidate of Science, Head of Department of Industrial Production Technologies of Far Eastern Federal University, Russia, Vladivostok
Boris Notkin
candidate of Science, Associate Professor of Department of Industrial Production Technologies of Far Eastern Federal University, Researcher of Institute of Automation and Control Processes FEB RAS, Russia, Vladivostok
Yuliya Oncha
Postgraduate student, the Department of Industrial Production Technologies, Far Eastern Federal University, Russia, Vladivostok
АННОТАЦИЯ
В работе предложен способ линеаризации объекта на этапе идентификации для получения прогнозирующей модели. Представлены результаты сравнительных экспериментов, подтверждающие эффективность предложенного решения.
ABSTRACT
In this paper we propose a method of linearization of the plant on the stage of identification to obtain a predictive model. Displaying results comparative experiments, confirming the effectiveness of the proposed solutions.
Ключевые слова: идентификация; прогнозирующее управление; прогнозирующая модель.
Keywords : identification; model predictive control; predictive model.
При синтезе систем управления широкое распространение получил метод прогнозирующего управления [3; 7]. Прогнозирующее управление предложено в 70-х годах прошлого века. Впоследствии MPC было успешно применено в промышленности в сфере управления технологическими процессами [9; 11]. Основное преимущество прогнозирующего управления — это возможность управлять многомерными и многосвязными объектами со сложной структурой, включающей нелинейности, оптимизировать процессы в режиме реального времени в рамках ограничений на управляющие и управляемые переменные, учитывать параметрические неопределенности объекта и возмущающих воздействий [6; 10].
Основной принцип прогнозирующего управления состоит в использовании математической модели объекта управления, на основе которой на каждом интервале дискретности ![]() отыскивается такая последовательность управляющих воздействий
отыскивается такая последовательность управляющих воздействий ![]() на горизонте прогноза
на горизонте прогноза ![]() , которая будучи приложена к объекту, обеспечит максимальное совпадение последовательности прогнозируемых значений выхода
, которая будучи приложена к объекту, обеспечит максимальное совпадение последовательности прогнозируемых значений выхода ![]() с последовательностью егозаданных значений
с последовательностью егозаданных значений ![]() . При этом из всей последовательности управляющих воздействий применяется только первое
. При этом из всей последовательности управляющих воздействий применяется только первое ![]() , затем горизонт прогноза сдвигается и вычисления повторяются.
, затем горизонт прогноза сдвигается и вычисления повторяются.
Последовательность управляющих воздействий вычисляется путем минимизации целевой функции на каждом интервале управления ![]() .Одна из общих форм целевой функции имеет вид [4; 8]:
.Одна из общих форм целевой функции имеет вид [4; 8]:


где:![]() — горизонт прогноза;
— горизонт прогноза;
![]() — прогноз выхода объекта на момент времени j, сделанный в момент времени
— прогноз выхода объекта на момент времени j, сделанный в момент времени ![]() ;
;
![]() — заданный выход объекта;
— заданный выход объекта;
![]() — амплитуда управления;
— амплитуда управления;
![]() ,
, ![]() и
и ![]() — весовые коэффициенты.
— весовые коэффициенты.
Прогноз выхода объекта осуществляется на базе прогнозирующей модели:
![]() ,
,
где ![]() — текущее состояние объекта управления, которое для прогнозирующей модели принимается в качестве ее начального состояния.
— текущее состояние объекта управления, которое для прогнозирующей модели принимается в качестве ее начального состояния.
Классическая схема прогнозирующей модели представлена на рис. 1.

![]() Рисунок 1. структурная схема прогнозирующей модели
Рисунок 1. структурная схема прогнозирующей модели
В случаях, когда состояние объекта измерить невозможно, либо измерения сильно зашумлены, используются различные методы для оценки текущего состояния объекта ![]() . Один из распространенных методов оценки состояния — это использование фильтра Калмала, для синтеза которого необходимо знание математической модели объекта и статистических характеристик погрешности измерения.
. Один из распространенных методов оценки состояния — это использование фильтра Калмала, для синтеза которого необходимо знание математической модели объекта и статистических характеристик погрешности измерения.
В случаях, когда математическая модель объекта неизвестна или известна не полностью, возникает необходимость решения дополнительной задачи — идентификация объекта. В случае линейности объекта существуют общие подходы идентификации, однако для нелинейных объектов пока что разработаны подходы, подходящие для частных объектов [2].
В данной статье предложен способ, позволяющий синтезировать прогнозирующую модель без априорных знаний математической модели объекта, а только по выборке вход/выход объекта.
Материал статьи организован следующим образом. В разделе 1 рассматривается теоретическая (классическая) реализация синтеза прогнозирующей модели по известному математическому описанию объекта. На основе теоретического решения в разделе 2 описана предлагаемая практическая методика синтеза прогнозирующей модели по экспериментальным данным вход/выход объекта. В разделе 3 представлены результаты сравнительных экспериментов.
1. Классическая методика синтеза прогнозирующей модели
Для осуществления прогноза выхода динамического объекта необходимо знание полного вектора его текущего состояния. На практике, как правило, вектор состояния объекта измеряется частично, при этом его элементы, не подлежащие прямому измерению, могут быть получены косвенно, путем оценки.
Для оценки текущего состояния объекта рассмотрим нерекурсивыный фильтр. Этот фильтр позволяет оценить текущее состояние объекта ![]() по его известному математическому описанию, управлениям
по его известному математическому описанию, управлениям ![]() и выходам
и выходам ![]() ,
,![]() на некотором ретроспективном горизонте
на некотором ретроспективном горизонте ![]() , предшествующему моменту времени
, предшествующему моменту времени ![]() . Структурная схема прогнозирующей модели для этого случая представлена на рис. 2.
. Структурная схема прогнозирующей модели для этого случая представлена на рис. 2.
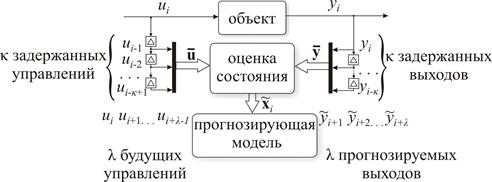
Рисунок 2. Структурная схема прогнозирующей модели
Далее представлено математического описание, синтеза нерекурсивного фильтра.
Пусть математическая модель объекта известна и представлена в дискретной форме пространства состояний:
|
|
(1) (2) |
где: ![]() — положительно определенные матрицы; в данном случае речь пойдет о SISO объекте.
— положительно определенные матрицы; в данном случае речь пойдет о SISO объекте.
Для оценки текущего состояния объекта воспользуемся доступной для измерения информацией о входах и выходах объекта на некотором предыдущем отрезке времени (ретроспективном горизонте), продолжительностью ![]() интервалов дискретности, как показано на рис. 3.
интервалов дискретности, как показано на рис. 3.
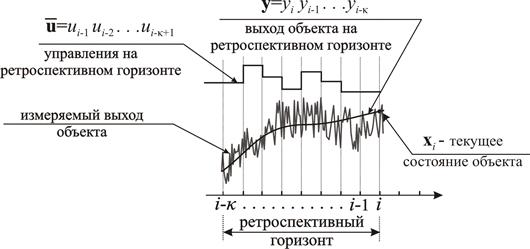
Рисунок 3. Оценка состояния
Величина ретроспективного горизонта κ, для линейного объекта должна быть не меньше, чем порядок этого объекта. На практике, обычно, ![]() выбирают существенно больше, что позволяет повысить обобщающие качества решения, функционирующего в условиях зашумленных входных данных.
выбирают существенно больше, что позволяет повысить обобщающие качества решения, функционирующего в условиях зашумленных входных данных.
С учетом того, что управления ![]() ,
,![]() известны, оценка состояния сводится к отысканию такого текущего состояния
известны, оценка состояния сводится к отысканию такого текущего состояния ![]() , при котором квадрат отклонения измеряемого выхода объекта
, при котором квадрат отклонения измеряемого выхода объекта ![]() ,
,![]() от восстановленного
от восстановленного ![]() ,
,![]() будет минимальный.
будет минимальный.
Минимизируемая целевая функция примет вид:
|
|
(3) |
где: ![]() — фактически измеряемый выход объекта
— фактически измеряемый выход объекта ![]() с учетом погрешности измерения
с учетом погрешности измерения ![]() ;
;
![]() — соответствующая оценка выхода объекта, выполненная с учетом известных управлений на горизонте прогноза
— соответствующая оценка выхода объекта, выполненная с учетом известных управлений на горизонте прогноза ![]() и зависящая от оценки текущего состояния
и зависящая от оценки текущего состояния ![]() объекта на этом отрезке времени.
объекта на этом отрезке времени.
Для того чтобы выразить оценку выхода динамической системы ![]() на ретроспективном горизонте
на ретроспективном горизонте
дипломов



Оставить комментарий