КИНЕТИЧЕСКАЯ  ЭНЕРГИЯ  НЕПОДВИЖНЫХ  ДЕБАЛАНСОВ  УПРАВЛЯЕМОЙ  ВИБРАЦИОННОЙ  МАШИНЫ

Черевко  Александр  Николаевич

канд.  техн.  наук,  зав.  кафедрой  теоретической  механики,  доцент  Полтавского  национального  технического  университета,  Украина,  г.  Полтава

E-mail: 

KINETIC  ENERGY  OF  THE  FIXED  UNBALANCES  THE  CONTROLED  VIBRATING  MACHINES

Alexandr  Cherevko

candidate  of  Science,  Head  of  Theoretical  Mechanics  department,  assistant  professor  of  Poltava  National  Technical  University,  Ukraine,  Poltava

АННОТАЦИЯ

Определяется  кинетическая  энергия  неподвижных  дебалансов  технологической  машины  с  двумя  управляемыми  дебалансными  вибровозбудителями.  Учитывается  их  сложное  движение  и  используются  вибрационные  оси.  Кинетическая  энергия  необходима  для  построения  математической  модели  на  основе  уравнений  Лагранжа  второго  рода.

ABSTRACT

Determined  by  the  kinetic  energy  of  the  fixed  unbalance  technological  machine  with  two  сontrolled  unbalanced  vibro-exciters.  Take  into  account  their  complex  motion  and  used  vibrating  axis.  Kinetic  energy  is  needed  to  build  a  mathematical  model  based  on  the  Lagrange  equations  of  the  second  kind.

Ключевые  слова:  дебаланс;  вибровозбудитель;  математическая  модель;  кинетическая  энергия.

Keywords:  eccentric  weight;  vibration  exciter;  mathematical  model;  the  kinetic  energy. 

Для  составления  математической  модели  сложной  механической  системы  воспользуемся  последовательностью  действий,  которая  определяется  уравнениями  Лагранжа  второго  рода  [2].

В  исследованиях  будет  использоваться  подвижная  система,  названная  проф.  Сердюком  Л.И.  вибрационной  [1].

где:    —  кинетическая  энергия  системы;

  —  обобщенная  координата  системы;

  —  обобщенная  скорость  системы;

  —  обобщенная  сила  системы.

Используем  такие  обобщенные  координаты:

,  ,    —  декартовые  координаты,  которые  определяют  перемещение  центра  масс  подвижного  корпуса  машины  вдоль  соответствующих  координатных  осей;

  —  угол,  который  определяет  поворот  подвижного  корпуса  в  горизонтальной  плоскости  вокруг  оси  ;

  —  угол,  который  определяет  поворот  подвижного  корпуса  в  вертикальной  профильной  плоскости  вокруг  оси  ;

  —  угол,  который  определяет  поворот  подвижного  корпуса  в  вертикальной  фронтальной  плоскости  вокруг  оси  ;

  —  угол,  который  определяет  поворот  дебалансного  вала  относительно  собственной  оси;

,    ,    —  декартовые  координаты,  которые  определяют  перемещение  центра  масс  обрабатываемой  среды,  вдоль  соответствующих  координатных  осей;

;  ;    —  декартовые  координаты,  которые  определяют  перемещение  центра  масс  обрабатываемой  среды.

Ранее  уже  была  определена  кинетическая  энергия  обрабатываемой  среды,корпуса  машины  и  дебалансных  валов.

Найдем  кинетическую  энергию  неподвижных  дебалансов.

Кинетическая  энергия  неподвижного  дебаланса  2.

Неподвижный  дебаланс  2  совершает  сложное  движение.  Вращаясь  вокруг  оси  дебалансного  вала  1  с  угловой  скоростью  ,  вместе  с  корпусом  совершает  свободное  движение:

.

где    —  абсолютная  скорость  центра  масс  дебаланса;

.

;

где  ,  ,    —  координаты  центра  масс  дебаланса;

,  ,  .

.    ;       .

.

;

;  ;  ;  .

;

;

;

Преобразуем  полученное  выражение

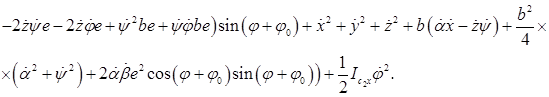
Кинетическая  энергия  неподвижного  дебаланса  5.

Неподвижный  дебаланс  5  совершает  сложное  движение.  Вращаясь  вокруг  оси  дебалансного  вала  2  с  угловой  скоростью  ,  вместе  с  корпусом  совершает  свободное  движение:

.

где    —  абсолютная  скорость  центра  масс  дебаланса;

.

;

где  ,  ,    —  координаты  центра  масс  дебаланса;

,,.

.    ;      

;

;

.         ;  ;  .

;

;

;

Преобразуем  полученное  выражение

Определим  кинетическую  энергию  неподвижных  дебалансов:

Учитывая  то,  что  неподвижные  дебалансы  одинаковые,  принимаем  следующие  обозначения:

Тогда:

Преобразуем  полученное  выражение:

где:

Кинетическая  энергия  неподвижных  дебалансов  имеет  вид:

Выводы

При  сложном  движении  вибрационной  машины  кинетическая  энергия  неподвижных  дебалансов  в  большей  степени  зависит  от  вращательного  движения,  чем  от  поступательного.

Список  литературы:

1.Сердюк  Л.І.,  Черевко  О.М.,  Давиденко  Ю.О.  Керовані  вібраційні  машини  з  дебалансними  збуджувачами  (теорія,  дослідження,  конструювання):  монографія  /  Л.І.  Сердюк,  О.М.  Черевко,  Ю.О.  Давиденко,  Полтава:  ТОВ  “АСМІ”,  2013.  —  370  с.

2.Яблонский  А.А.  Курс  теоретической  механики  /  Ч.  II.  Динамика:  Учебник  для  техн.  вузов.  6-е  изд.,  испр.  М.:  Высш.  шк.,  1984.  —  423  с.