Статья опубликована в рамках: XLVII Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 29 июня 2015 г.)
Наука: Технические науки
Секция: Информатика, вычислительная техника и управление
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
ПАРАМЕТРИЧЕСКАЯ ИДЕНТИФИКАЦИЯ И МОДЕЛИРОВАНИЕ ЭЛЕКТРОГИДРАВЛИЧЕСКОЙ СЛЕДЯЩЕЙ СИСТЕМЫ УПРАВЛЕНИЯ
Карапетьян Валерий Артёмович
канд. техн. наук, доцент
Севастопольского государственного университета,
РФ, г. Севастополь
PARAMETRIC IDENTIFICATION AND MODELING OF ELECTROHYDRAULIC SERVO CONTROL SYSTEM
Valery Karapetyan
candidate of Technical Sciences, Associate Professor of
Sevastopol State University,
Russia, Sevastopol
АННОТАЦИЯ
Описана процедура определение параметров передаточной функции силовой части гидропривода по данным эксперимента. Приведены результаты верификации модели электрогидравлической следящей системы путём компьютерного моделирования. Идентификация и моделирование проводились стандартными средствами пакета Matlab.
ABSTRACT
Procedure determination of parameters transfer function power part of a hydraulic actuator according to experiment is described. Results of verification model of the electrohydraulic servo system by computer modeling are given. Identification and modeling was conducted using the standard Matlab package.
Ключевые слова: идентификация; моделирование; следящая система; Matlab.
Keywords: identification; modeling; servo system; Matlab.
Постановка задачи и описание объекта исследования
Рассматривается следящая электрогидравлическая система управления, решающая задачу наведения объекта в горизонтальной плоскости. Исполнительным устройством следящей системы является силовой электрогидропривод (СЭГП) объемного регулирования [1; 4; 5]. Гидропривод предназначен для преобразования электрических сигналов управления во вращение вала гидромотора, механически связанного через редуктор с объектом управления — горизонтальной поворотной платформой.
Функциональная схема следящей системы управления с СЭГП [3] приведена на рисунке 1.

Рисунок 1. Функциональная схема СЭГП
Здесь приняты следующие обозначения:
· 1, 2 — вращающиеся трансформаторы, установленные в задающем устройстве и на выходном вале гидромотора;
· 3, 4 — измерительные тахогенераторы, связанные с задающим устройством и с выходным валом гидромотора;
· 5, 6 — электронный усилитель-сумматор и электрогидравлический усилитель (устройство управления гидронасосом);
· 7, 8 — гидронасос, гидромотор;
· 9, 10 — механический редуктор и объект управления (поворотная платформа).
пунктирными линиями обозначены механические связи, а сплошными — электрические и гидравлические связи;
· ![]() — угол поворота входного вала (задающего устройства);
— угол поворота входного вала (задающего устройства);
· ![]() — угол поворота вала гидромотора (выходного вала);
— угол поворота вала гидромотора (выходного вала);
· ![]() — сигнал принимающего вращающегося трансформатора, пропорциональный величине угла (ошибке) рассогласования;
— сигнал принимающего вращающегося трансформатора, пропорциональный величине угла (ошибке) рассогласования;
· ![]() — сигнал, пропорциональный угловой скорости вращения входного (задающего) вала;
— сигнал, пропорциональный угловой скорости вращения входного (задающего) вала;
· ![]() — сигнал, пропорциональный угловой скорости вращения вала гидромотора.
— сигнал, пропорциональный угловой скорости вращения вала гидромотора.
Собственно силовая часть электрогидропривода (гидронасос‑гидромотор) представлена на схеме двумя блоками 7 и 8.
При наличии рассогласования между задающим (1) и принимающим (2) вращающимися трансформаторами измерительного устройства на вход усилителя (6) поступает сигнал, напряжение которого пропорционально углу рассогласования q, далее он усиливается до необходимой величины и поступает на обмотки электромагнита гидроусилителя гидропривода в виде разности токов определенной полярности. На усилитель также поступает сигнал рассогласования по угловым скоростям вращения задающего (3) и выходного (4) валов. Гидроусилитель поворачивает люльку насоса, обеспечивающего соответствующую производительность, а следовательно, скорость и направление вращения вала гидромотора, связанного с исполнительной осью горизонтальной платформы.
Силовая часть привода в линейном приближении может быть представлена математической моделью в виде последовательного соединения передаточных функций электрогидравлического усилителя и силового гидропривода (гидронасос‑гидромотор), при этом вид этих передаточных функций соответствует динамическим звеньям, приведенным в [3; 4]. На рисунке 2 приведена структурная схема силовой части привода

Рисунок 2. Структурная схема силовой части привода
На рисунке 2 приняты следующие обозначения:
· ![]() — разность токов во входных цепях электромеханического преобразователя;
— разность токов во входных цепях электромеханического преобразователя;
· ![]() ,
, ![]() — коэффициент усиления и постоянная времени электрогидравлического усилителя (устройства управления гидронасосом);
— коэффициент усиления и постоянная времени электрогидравлического усилителя (устройства управления гидронасосом);
· — угол поворота люльки гидронасоса;
· ![]() — коэффициент усиления (по скорости) силового гидропривода;
— коэффициент усиления (по скорости) силового гидропривода;
· ![]() — постоянная времени силового гидропривода;
— постоянная времени силового гидропривода;
· ![]() — коэффициент демпфирования силового гидропривода;
— коэффициент демпфирования силового гидропривода;
· ![]() — угловая скорость вращения вала гидромотора.
— угловая скорость вращения вала гидромотора.
Процедуры подготовки данных и идентификации
Для определения (идентификации) числовых значений параметров передаточных функций была проведена серия натурных экспериментов на реальном объекте и системе автоматического управления. Суть экспериментов состояла в том, чтобы в процессе отработки системой управления объектом различных заданных тестовых движений, зафиксировать изменения некоторых, значимых для процесса идентификации параметров передаточных функций, сигналов.
Входной сигнал ![]() (угол поворота задающего вала) для системы слежения формировался в виде линейно нарастающего сигнала. Задавались начальное и конечное значения углового положения горизонтальной платформы и время изменения угла от начального до конечного значений. Измеряемые электрические сигналы подавались на входы АЦП и фиксировались в числовых файлах. Данные во всех экспериментах снимались в течение фиксированного промежутка времени ~ 2800 мС.
(угол поворота задающего вала) для системы слежения формировался в виде линейно нарастающего сигнала. Задавались начальное и конечное значения углового положения горизонтальной платформы и время изменения угла от начального до конечного значений. Измеряемые электрические сигналы подавались на входы АЦП и фиксировались в числовых файлах. Данные во всех экспериментах снимались в течение фиксированного промежутка времени ~ 2800 мС.
Для проведения процедур идентификации параметров передаточных функций (рисунок 2) необходимо иметь отсчеты двух сигналов:
· сигнала Di, поступающего на обмотки электромагнитного преобразователя (Di=i1-i2 — разность токов двух обмоток электромагнита), который управляет положением заслонки в схеме гидроусилителя дроссель‑заслонка;
· сигнала w принимающего тахогенератора (модулирован частотой 400 Гц), пропорционального угловой скорости вращения вала гидромотора.
Сигнал, пропорциональный углу поворота люльки гидронасоса x не потребуется для идентификации параметров, так как соединение двух передаточных функций представляет собой неизменяемую часть силового привода и можно будет заменить последовательность этих звеньев одним динамическим звеном третьего порядка. Управляющий сигнал электромеханического преобразователя Di модулирован частотой 70±30 Гц. Модуляция применяется для предотвращения "залипания" заслонки в системе сопло‑заслонка.
В качестве примера числовых данных натурных экспериментов приведем, в графической форме, отсчеты сигналов aвх, Di, w.

Рисунок 3. Графики экспериментальных значений сигналов aвх, Di , w
Входное значение aвх равномерно изменяется от нуля до 25 градусов (верхний график). Разность токов Di обмоток магнитных катушек — управляющий сигнал электромеханического преобразователя, модулированный частотой 70 Гц (средний график). Сигнал угловой скорости w вала гидромотора, модулированный частотой 400 Гц (нижний график). Длительность записи каждого из сигналов — около 2,8 секунды.
Проведение процедуры идентификации параметров передаточной функции силовой части привода (рисунок 2) требует предварительной обработки выходного сигнала w, которая включает определение момента времени начала процесса идентификации и демодуляции сигнала w выходного тахогенератора.
Момент начала процесса идентификации определить сравнительно легко по началу изменения входного сигнала aвх. Он выбран равным 200 мС или 1280 отсчетов с начала записи данных экспериментов.
Поиск приемлемого метода демодуляции выходного сигнала w проводился по трем направлениям:
1. прямое применение функции демодуляции demod пакета Matlab [7];
2. методами цифровой частотной обработки [6; 8] — построением амплитудно-частотного спектра сигнала и, с помощью цифровой фильтрации (цифровыми фильтрами), удалением соответствующих частотных составляющих сигнала;
3. выделением огибающей путём оконтуривания рисунка графика [8] модулированного сигнала с последующей коррекцией, вызванной учетом направления поворота горизонтальной платформы.
Для успешной работы функции демодуляции demod необходимо более или менее точное значение частоты модуляции. В данном случае она должна быть равна 400 Гц. Однако в зависимости от номера эксперимента величина частоты модуляции менялась в пределах ±20 Гц, более того, для некоторых экспериментов не удавалось подобрать частоту модуляции даже на период длительности самого эксперимента. Поэтому данный метод был отвергнут.
Второй метод проведения «демодуляции» основывался на частотной обработке исходного сигнала цифровыми фильтрами низкой частоты. Применялись стандартные средства Matlab [6; 8] для реализации как БИХ‑, так и КИХ‑фильтров (функции ellip и fir1, соответственно) и прохождения сигнала w через цифровой фильтр (функция filter). Этот приём удаления из сигнала w несущей частоты удовлетворительных результатов не дал. На рисунках 4а и 4б приведены примеры частотной фильтрации сигнала, пропорционального угловой скорости вала гидромотора.
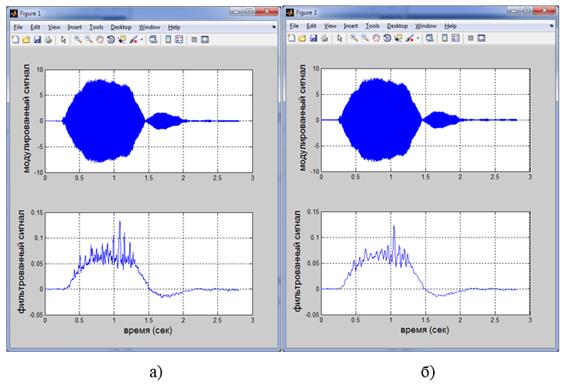
Рисунок 4. Исходный сигнал w и результаты цифровой фильтрации. а) обработка ФНЧ с КИХ‑фильтром, б) обработка ФНЧ с БИХ‑фильтром
Третье направление поиска процедуры «демодуляции» сигнала угловой скорости выходного вала w основывалось на идее получения огибающей модулированного сигнала путём оконтуривания изображений графиков измерений w, представленных в виде, приведенном на рисунке 5.
Алгоритм выделения огибающей для получения "демодулированного" сигнала w включает следующие шаги:
а. построение графика сигнала w (верхняя часть рисунка 5);
б. сохранение графика сигнала в виде файла‑изображения в формате bmp;

Рисунок 5. Процедура демодуляции
в. дополнительная обработка изображения в обычном графическом редакторе, например в Paint. Цель обработки состоит в том, чтобы в изображении графика сигнала в поле объекта figure оставить только само изображение, убрав оцифрованные оси и преобразовав многоцветное изображение к бинарному (черно‑белому);
г. обработка полученного в пункте в) изображения в пакете Matlab функцией выделения контура изображения imcontour [9] и получение массива с координатами точек контура (средняя часть рисунка 5). Здесь следует заметить, что после такой обработки теряется связь значений координат точек контура с физическими единицами, например, горизонтальной координаты точек контура с временной переменной;
д. сохранение массива с координатами точек контура изображения в текстовом файле для дальнейшей обработки;
е. загрузка данных текстового файла с огибающей в Matlab‑программу и приведение массива данных к истинным временным и амплитудным отсчётам масштабированием и с помощью аппроксимирующего сглаживающего кубического сплайна (функция csaps) и вычисления значений огибающей сигнала во временных дискретах (функция fnval) [2];
ж. массив точек огибающей сигнала (нижняя часть рисунка 5) упаковывался в текстовый файл и в дальнейшем использовался как исходный набор числовых данных в алгоритмах идентификации математических моделей силового привода.
Сравнивая все три метода выделения огибающей сигнала w и опираясь на опыт применения их к обработке всего объема экспериментальных данных, решено было остановиться на последнем. Этот метод наиболее трудоёмок — он требует использования нескольких сложных и «капризных» функций Matlab и программ графической обработки изображений. Однако каждый шаг алгоритма может визуально контролироваться исследователем путем сравнения получающихся графиков с исходным графиком модулированного сигнала w.
После предварительной обработки экспериментальных данных и фиксации их в числовой форме, соответствующей нижнему графику рисунка 5, была проведена процедура идентификации параметров передаточных функций силовой части гидропривода.
В процессе выполнения процедуры идентификации для всех наборов экспериментальных данных было установлено, что наиболее устойчивые и адекватные результаты получаются для двух видов передаточных функций —
![]() и
и ![]() . (1)
. (1)
Две цифры, составляющие индексы передаточных функций означают соответственно порядки полиномов числителя и знаменателя.
В нашем случае удобнее представлять передаточную функцию в виде набора коэффициента усиления К, постоянных времени Т или t и коэффициентов демпфирования x.
Для передаточных функций третьего порядка —
![]()
или ![]() ; (2)
; (2)
для передаточных функций четвертого порядка —
|
|
(3) |
|
или |
|
|
или |
Результаты идентификации и моделирования
Параметрическая идентификация передаточных функций вида (1), проведенная по данным всех экспериментов показала, что наиболее адекватными являются передаточные функции в виде (2) и (3).
Процедура идентификации проводилась программными средствами пакета System Identification Toolbox [7] системы Matlab, в частности, функцией tfest – оценки параметров передаточных функций по временным откликам. Качество идентификации оценивалось величиной соответствия fit
 , (4)
, (4)
где: y — исходные (экспериментальные) выходные данные;
![]() — выход идентифицированной передаточной функции;
— выход идентифицированной передаточной функции;
![]() — усредненное значение массива y.
— усредненное значение массива y.
На рисунке 6 представлены графики, иллюстрирующие характерные результаты процедуры идентификации параметров передаточной функции по данным одного из экспериментов

Рисунок 6. Экспериментальный и модельные графики угловой скорости w с указанием процентных значений величин соответствия, z 0p3 — идентификатор передаточной функции вида ![]() ; z1p4 — идентификатор передаточной функции вида
; z1p4 — идентификатор передаточной функции вида ![]()
Из графиков рисунка 6 следует, что уровень адекватности модельных (синий и зеленый цвета) и экспериментальных (серый цвет) данных весьма высок (более 94 %). Практическое совпадение значений величин соответствия 94,51 % и 94,74 % позволяет сделать вывод о том, что значения постоянных времени T1 и t1 в выражении (3) близки. Похожие результаты справедливы для всех наборов экспериментальных данных. Данный факт приводит к необходимости выбора передаточной функции силовой части гидропривода в виде (2) [4; 5].
Аналогичные результаты были получены и с помощью специальной графической утилиты Ident из расширения System Identification Toolbox пакета Matlab, представляющей собой интерактивный программный инструмент для решения широкого круга задач идентификации динамических объектов и процессов [7].
Результаты идентификации передаточных функций позволили провести моделирование движения силовой части гидропривода (изменение скорости вала гидромотора w). Интегрируя модельную угловую скорость w и учитывая передаточное число выходного механического редуктора (рисунок 1, блок 9), было проведено сравнение угловых характеристик экспериментального входного задающего процесса aвх и модельного выходного aвых. Один из примеров такого сравнения приведен на рисунке 7.

Рисунок 7. Графики экспериментального aвх и модельных aвых
Характер взаимного поведения входных aвх и выходных aвых угловых характеристик обусловлен тем фактом, что экспериментальные данные снимались с действующего образца следящей электрогидравлической системы управления, обладающей астатизмом.
Заключение
Предложенная процедура предварительной подготовки экспериментальных данных и средства пакета Matlab для параметрической идентификации динамических объектов позволили эффективно решить поставленную задачу. Полученные результаты достаточно хорошо согласуются с данными из литературных источников, что подтверждает адекватность выбранного подхода и инструментария.
Список литературы:
1.Гамынин М.С. Гидравлический привод систем управления. М.: Машиностроение, 1972. — 376 с.
2.Кетков Ю.Л. Matlab 7: программирование, численные методы / Ю.Л. Кетков, А.Ю. Кетков, М.М. Шульц. СПб.: БХВ‑Петербург, 2005. — 752 с.
3.Описание изобретения к Патенту РФ № 2004114986/09, 17.05.2004 [Электронный ресурс] — Режим доступа. — URL: http://www.freepatent.ru/images/patents/201/2268480/ patent-2268480.pdf
4.Потапов А.М. Основы расчета и проектирования линейных следящих систем. Л.: ЛМИ, 1980. — 96 с.
5.Прокофьев В.Н., Данилов Ю.А., Кондаков Л.А. Аксиально-поршневой регулируемый гидропривод. М.: Машиностроение, 1969. — 496 с.
6.Сергиенко А.Б. Цифровая обработка сигналов. СПб.: Питер, 2002. — 608 с.
7.Ljung L. System Identification Toolbox. User’s Guide. MathWorks, 2012. — 818 p.
8.Signal Processing Toolbox. User’s Guide. MathWorks, 2012. — 527 p.
9.Image Processing Toolbox. Reference. MathWorks, 2012. — 881 p.
дипломов


Оставить комментарий