УПРАВЛЯЕМОЕ  ДВИЖЕНИЕ  МАЛОГО  ТЕЛА  В  СИЛОВОМ  ПОЛЕ  НЬЮТОНА

Бабаджанянц  Левон  Константинович

д-р  физ.-мат.  наук,  профессор  Санкт-Петербургского  государственного  университета,  РФ,  г.  Санкт-Петербург

E -mail:  levon@mail.wplus.net

Брэгман  Анна  Михайловна

студент  Санкт-Петербургского  государственного  университета,  РФ,  г.  Санкт-Петербург

E -mail:  meune@mail.ru

Брэгман  Константин  Михайлович

старший  преподаватель  Санкт-Петербургского  государственного  университета,  РФ,  г.  Санкт-Петербург

E -mail:  beswdw@gmail.com

Петросян  Леон  Аганесович

д-р  физ.-мат.  наук,  профессор  Санкт-Петербургского  государственного  университета,  РФ,  г.  Санкт- Петербург

E-mail: 

CONTROLLED  MOTION  OF  A  SMALL  BODY  IN  NEWTONIAN  FORCE  FIELD

Levon  Babadzanjanz

doctor  of  Science,  professor  of  Saint-Petersburg  State  University,  Russia,  Saint-Peretsburg

Anna  Bregman

student  of  Saint-Petersburg  State  University,  Russia,  Saint-Peretsburg

Konstantin  Bregman

senior  Lecturer  of  Saint-Petersburg  State  University,  Russia,  Saint-Peretsburg

Leon  Petrosyan

doctor  of  Science,  professor  of  Saint-Petersburg  State  University,  Russia,  Saint-Peretsburg

Работа  выполнена  при  поддержке  гранта  СПбГУ  9.37.345.2015.

АННОТАЦИЯ

  Предложенный  нами  ранее  алгоритм  решения  уравнений  в  вариациях  для  задачи  о  движении  материальной  точки  в  центральном  силовом  поле  с  возмущением  используется  в  настоящей  работе  для  получения  возмущений  первого  порядка  в  декартовых  координатах  малого  тела,  движущегося  в  силовом  поле  Ньютона  и  управляемого  кусочно-постоянной  малой  тягой. 

ABSTRACT

  In  this  study  based  on  the  algorithm  of  solution  of  equations  of  variations  for  the  problem  of  motion  of  a  point  mass  in  a  perturbed  central  force  field  that  has  been  proposed  earlier,  we  obtain  the  first  order  perturbations  of  Cartesian  coordinates  of  a  small  body  moving  in  Newtonian  force  field  under  a  piecewise-constant  low  thrust. 

Ключевые  слова :  уравнения  в  вариациях;  поле  Ньютона;  уравнения  движения;  возмущения;  кусочно-постоянная  малая  тяга.

Keywords:  equations  of  variations;  Newtonian  field;  equations  of  motion;  perturbations;  piecewise-constant  low  thrust. 

1.  Введение

В  статье  [1]  был  предложен  метод  решения  уравнений  в  вариациях  в  декартовых  координатах  для  случая  движения  материальной  точки  в  произвольном  возмущенном  центральном  поле.  В  настоящей  работе  этот  метод  при-меняется  в  задаче  об  управляемом  малой  тягой  движении  малого  тела  в  цен-тральном  поле  Ньютона  для  построения  возмущений  первого  порядка.

  Мы  рассмотрим  управляемое  кусочно-постоянной  малой  тягой  движение  малого  тела  массы    в  точечном  поле  притяжения  Солнца  в  относительной  декартовой  системе  координат    (ее  центр  совпадает  с  Солнцем)  и  будем  далее  использовать  астрономические  единицы  длины  (а.е.),  массы  (масса  Солнца  равна  1)  и  времени  (сутки).  Невозмущенную  орбиту  тела  будем  считать  эллиптической.  Соответствующие  возмущенная  и  невозмущенная  задачи  Коши  будут  следующими  [2;  3]:

,  (1)

,  (2)

,      (3)

где    —  компоненты  малой  тяги    —  истинная  аномалия  эл-липтической  задачи  двух  тел  (2),(3),  ,    а    —  грави-тационная  постоянная  Гаусса  (=0,01720209895  в  астрономической  системе  единиц).  В  рассматриваемом  здесь  случае  центрального  поля  Ньютона  уравнения  для  возмущений    и  уравнения  для    можно  получить  из  уравнений  (6)  и  (11)  работы  [1],  положив  там  ,    (а  также  ,  см.  (3)):

  (4)

  (5)

Рассмотрим  уравнение

,  (6)

где    —  истинная  аномалия  эллиптической  задачи  двух  тел  [2;  3],  определяемой  уравнениями:

Решение  уравнения  (6)  можно  найти  в  [5]  (см.  также  [2;  3]):

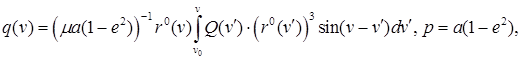
где:    —  параметр,  полуось  и  эксцентриситет  эллиптической  орбиты.

Используя  (7),  выпишем  решения  уравнений  (4),  (5):

  (7) 

  (8) 

Далее  мы  будем  использовать  следующее  представление  решения  задачи  двух  тел  [2;  3]:

,    (9) 

,  , 

где:    —  истинная  и  эксцентрическая  аномалии, 

  —  элементы  эллиптической  орбиты,  определяемой  задачей  Коши  (2),  (3)  (полуось,  экс-центриситет,  долгота  восходящего  узла,  аргумент  широты,  наклонение  и  сред-няя  аномалия  в  эпоху  ). 

Кроме  того,  нам  понадобятся  следующие  формулы  [2;  3;  4]:

  (10)

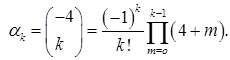
2.  Движение  малого  тела  в  поле  Ньютона  под  действием  кусочно-постоянной  малой  тяги

Рассмотрим  малую  тягу    в  виде: 

  (11)

где    а    —  функция  Хэвисайда.  Это  означает,  что  в  качестве  компонент  ускорений  от  малой  тяги  малого  тела  (см.  (1))  мы  будем  рассматривать  функции  .  Учитывая  это  и  полагая  ради  простоты  ,  можно  переписать  формулы  (7),  (8)  в  виде:

  (12)

  (13)

где    —  символ  Кронекера.

Чтобы  упростить  эти  формулы  введем  в  рассмотрение  девять  функций:

Используя  (9),  получаем:

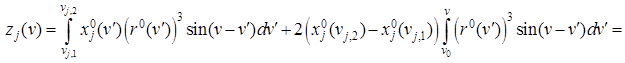
Таким  образом,  мы  выразили  правые  части  в  (12),  (13)  в  терминах  введенных  функций.

Так  как  эти  функции  ,,,,,,,,  не  могут  быть  вычислены  в  подходящем  виде  непосредственно  при  помощи  систем  компьютерной  алгебры,  мы  выразим  их  приближенно  в  терминах  следующих  (более  простых  в  этом  смысле)  функций:

,

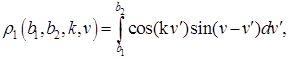
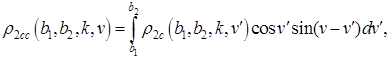
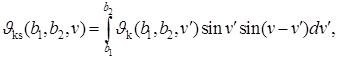
Действительно,  используя  эти  функции  и  формулы  (9),  (10),  получаем:

1.    

2. 

3. 

4. 

.

5. 

.

6. 

.

7. 

.

8.    

.

9. 

.

3.  Заключение

Таким  образом,  мы  получили  формулы  для  возмущений  первого  порядка  в  относительных  декартовых  координатах  малого  тела,  движущегося  под  дейст-вием  кусочно-постоянного  управления  в  центральном  поле  Ньютона.  Это  фор-мулы  (12),  (13),  которые  легко  вычисляются  средствами  таких  программ  компьютерной  алгебры  как,  например,  Wolfram  Mathematica  [7]  или  Maple  [6],  так  как  их  правые  части  выражаются  через  функции  ,,,,,,  ,,,  которые  непосредственно  вычисляются  в  этих  программах  через  элементарные  функции.  Очевидно,  что  полученные  результаты  для  одноимпульсной  малой  тяги  легко  обобщить  и  на  случай  многоимпульсной  малой  тяги,  последовательно  применяя  формулы  (12),  (13). 

Список  литературы:

1. Бабаджанянц  Л.К.,  Брэгман  А.М.,  Брэгман  К.М.,  Касикова  П.В.  Об  уравнениях  в  вариациях  в  задаче  о  движении  точки  в  возмущенном  центральном  поле  //  НП  «Сибак»,  Сборник  статей  XXXI  Межд.  Конф.,  Секция  7:  Аэрокосмическая  техника  и  технологии.  —  2014.  —  №  2(27).  —  C.  83—91.
2. Брауэр  Д.,  Клеменс  Д.  Методы  небесной  механики  —  М.:  Мир,  1964.  —  515  с.
3. Субботин  М.Ф.  Введение  в  теоретическую  астрономию  —  М.:  Наука,  1968.  —  800  с.
4. Холшевников  К.В.,  Титов  В.Б.  Задача  двух  тел  —  СПб:  Изд.  СПбГУ,  2007.  —  180  с.
5. Hill  G,  A  Method  of  Computing  of  Absolute  Perturbations  //  Astr.  Nachr.,  83.  1874.  —  P.  209—224. 
6. 6.            Maplesoft  Documentation  Center  [Электронный  ресурс]  —  Режим  доступа.  —  URL:  http://www.maplesoft.com/documentation_center/
7. 7.            Wolfram  Mathematica  Documentation  Center  [Электронный  ресурс]  —  Режим  доступа.  —  URL:http://reference.wolfram.com/mathematica/guide/Mathematica.html