Статья опубликована в рамках: XV Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 12 ноября 2012 г.)
Наука: Технические науки
Секция: Приборостроение, метрология, радиотехника
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
ИССЛЕДОВАНИЯ В ОБЛАСТИ ОБРАБОТКИ МИКРОКОМПОНЕНТОВ И МИКРОДЕТАЛЕЙ НА ОБРАБАТЫВАЮЩИХ ЦЕНТРАХ
Диордица Ирина Николаевна
ассистент кафедры производства приборов
Национальный технический университет Украины,
«Киевский политехнический институт», г. Киев
E-mail: indior@yandex.ru
RESEARCHES IN AREA OF TREATMENT MIKROCOMPONENTS AND MIKRODETAILS ON PROCESSING CENTERS
Iryna Diorditsa
National Technical University of Ukraine
“Kyiv Polytechnic Institute”, Kiev
АННОТАЦИЯ
В статье рассматриваются способы микрообработки. Исследуются методы точности обработки для типовых микромеханических компонентов. Проведены исследования математических моделей для прецизионной обработки.
ABSTRACT
In the article methods are examined mikrotreatments. The methods of exactness of treatment are probed for a model mikromechanical components. Studies of mathematical models for precision machining.
Ключевые слова: микрокомпонент; способы микрообработки; методы
Keywords: mikrocomponent; methods mikrotreatments; methods
Вступление.
Микросистемные технологии рассматриваются сегодня как ключевые технологии с экономическим потенциалом. Согласно результатам маркетинговых исследований эти технологии развиваются в США, Японии и Германии. В США, где сильно развита микроэлектроника, особенно развивается производство комплектующих на базе микросистем, в Германии большое развитие получили прикладные направления и микросистемные технологии. В Японии миниатюризация всегда была приоритетным направлением в развитии производства, поэтому сегодня практически в каждой крупной японской компании есть научное подразделение, которое занимается проблемами микросистемных компонентов [2].
Постановка задачи.
Типовые микромеханические компоненты требуют обработки с точностью от 0,1 до 1 мкм. Такая высокая точность изготовления этих компонентов с трудом может быть достигнута даже на прецизионных станках. Поэтому технологический процесс обработки должен включать дополнительные модели изготовления микромеханических компонентов, которые компенсируют возникновение технологической погрешности [1].
Вследствие роста необходимости обеспечения высокой точности, одновременно связанной со снижением себестоимости, возникает необходимость в промышленном оборудовании с возможностью компенсации геометрических погрешностей, что регистрируется измерительной техникой в режиме реального времени. Исследование возникновения векторного характера погрешности на станках.
Исследование этого вопроса доказало, что, например, образцовый элемент ![]() расположенный в рабочем пространстве оборудования и при измерении в его системе координат с помощью той же системы отсчета даст размер
расположенный в рабочем пространстве оборудования и при измерении в его системе координат с помощью той же системы отсчета даст размер![]() , который будет отличаться от образца. В общем случае всегда будет выполняться неравенство
, который будет отличаться от образца. В общем случае всегда будет выполняться неравенство ![]() (рис. 1). При этом
(рис. 1). При этом ![]() следует воспринимать как нестандартную меру измерения, которая принадлежит станку. Перемещение образцового элемента в рабочем пространстве будет давать соответствующую погрешность измерения которые, снова таки, в общем случае будут колебаться, например, как случайная величина с нормальным законом распределения, то есть
следует воспринимать как нестандартную меру измерения, которая принадлежит станку. Перемещение образцового элемента в рабочем пространстве будет давать соответствующую погрешность измерения которые, снова таки, в общем случае будут колебаться, например, как случайная величина с нормальным законом распределения, то есть ![]() (рис. 1).
(рис. 1).

Рисунок 1. Розсеивание размеров LB в зависимости от расположения образцовой меры на столе

Рисунок 2. Результаты исследования точности полученные на фрезерном столе в координатах X (a), Y (б)
Если рассмотреть этот процесс в двух координатах, то движение при измерении и итоговую погрешность можно представить как сумму векторов движений:
![]() и
и ![]() . (1)
. (1)
Исследования доказали, что векторная сумма при прямом и обратном движении не является зеркальным отображением друг друга (рис. 2). Объяснение здесь может быть только одно: технологическое оборудование имеет различные нагрузки при противопо-ложных направлениях движения и как следствие разную величину износа рабочих частей. Особенно важным явлением при этом является неодинаковая точность вдоль всей длины по координатам, которая усиливается со временем работы станка. Вектор погрешности при этом может иметь описание как эллипсоидальная зависимость в координатах ![]() . В частных случаях эллипс может менять местами свою большую и малую ось, а также упрощаться до окружности (рис. 3):
. В частных случаях эллипс может менять местами свою большую и малую ось, а также упрощаться до окружности (рис. 3):


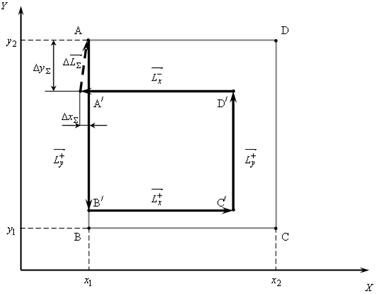
Рисунок 3. Поле рассеивания векторных диаграмм в зависимости от измерения, отклонения векторного идеального квадрата и векторной ошибки ![]() при контурной обработки инструмента
при контурной обработки инструмента
 (2)
(2)
где ![]() и
и ![]() — среднестатистические отклонение размера от образцовой
— среднестатистические отклонение размера от образцовой ![]() ,
,
![]() — угол вектора погрешности
— угол вектора погрешности ![]() или
или ![]() от вектора
от вектора ![]() .
.
Если использовать закон нормального распределения для случайной величины по координатам, то:
 (3)
(3)
(4)
На рисунке (рис. 3) видно, что выполнение комплексного движения щупа по двум координатам ![]() и
и ![]() , например, с точек D или B приведет к неправильной реализации геометрической фигуры типа «квадрат» в пространстве станка. Схождение векторов
, например, с точек D или B приведет к неправильной реализации геометрической фигуры типа «квадрат» в пространстве станка. Схождение векторов ![]() и
и ![]() практически невозможно. Так, например, контурная обработка или движение по линии ABCDА| (рис. 3) всегда будет приводить к| появлению вектора погрешности
практически невозможно. Так, например, контурная обработка или движение по линии ABCDА| (рис. 3) всегда будет приводить к| появлению вектора погрешности ![]() , который будет следствием влияния замкнутой окружности векторов:
, который будет следствием влияния замкнутой окружности векторов:
 . (5)
. (5)
Для устранения этого явления вводится термин зонной точности станка через понятие градиента. В таком случае это предоставит возможность ограничивать координаты объема, где точность позиционирования будет учитываться через векторные градиенты точности.
Заключение
Проведенные исследования математических моделей для прецизионной обработки микротехнических изделий и созданная методика и алгоритмы для моделирования погрешности обработки, с целью их компенсации с помощью компьютерного управления показывает, что в следствии необходимости обеспечения высокой точности, одновременно связанной со снижением себестоимости, возникает необходимость в промышленном оборудовании и возможность компенсации геометрических погрешностей, которая регистрируется измерительной техникой в режиме реального времени. Разработана конструкция для координатной привязки поля погрешностей и инструмента к системе координат станка и методика учета погрешностей при выполнении работ на станке. Разработана методика учета погрешности позиционирования на станке. Предложенная методика позволила уменьшить среднее отклонение полученных размеров от 60 мкм.
Список литературы:
1.Остафьев В.А., Диордица И.Н. Исследование точности обработки микромеханических компонентов. Вісник НТУУ "КПІ". Серія приладобудування. — Київ. 2006. — Вип. 32. — 172 с.
2.Kartunov S., Mechanische Mikrofertigungsverfahren — Übersicht, Besonderheiten, Auswahl, Anwendungen, Beispiele, Potentiale, Entwicklung. Ilmenau, Internationalen Wissenschaftliches Kolloquium Technische Universität Ilmenau 23.—26 September 2002, 234 с., ISSN 0943-7207.
дипломов


Оставить комментарий