Статья опубликована в рамках: XVIII Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 20 февраля 2013 г.)
Наука: Технические науки
Секция: Информатика, вычислительная техника и управление
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
МЕТОДИКА РАСЧЕТА ОТКАЗОУСТОЙЧИВОСТИ СИСТЕМ УПРАВЛЕНИЯ ТП
Имаев Дамир Хабибович
д-р техн. наук, профессор кафедры Автоматики и процессов управления (АПУ), СПбГЭТУ, г. Санкт-Петербург
E-mail: Damir.Imaev@mail.ru
Шестопалов Михаил Юрьевич
проректор по научной работе, канд. техн. наук, доцент кафедры Автоматики и процессов управления (АПУ), СПбГЭТУ, г. Санкт-Петербург
E-mail: Shestopalov08@mail.ru
METHOD OF TECHNOLOGICAL PROCESS CONTROL SYSTEMS FAULT-TOLERANCE CALCULATING
Imaev Damir
D.Sc., professor of Automation and control processes Department
Shestopalov Mikhail
Vice Rector for Science and Research of Saint-Petersburg Electrotechnical University “LETI”
АННОТАЦИЯ
Разрабатывается методика расчета отказоустойчивости систем управления технологическими процессами (СУ ТП) на основе конечного автомата типа Мура. Pассматривается изменение технического состояния СУ ТП после первой, второй неисправностей и последовательности неисправностей. Методика базируется на концепции множества стационарных моделей. Как формальное описание жизненного цикла СУ ТП рассматривается граф автомата для потока из трех потенциальных неисправностей. Сделан вывод о том, что проектирование СУ ТП представляет собой реконфигурирование, связанное с выбором точек измерения, обеспечивающих наблюдаемость состояний, точек введения управляющих воздействий, которые удовлетворяют условию управляемости, и синтезом алгоритма принятия решений.
ABSTRACT
In the article is designed the method of technological process control systems fault-tolerance calculating (TP CS) based on finite state machine of Moore type. Is observed the TP CS technical condition state change after the first, second failure and the sequence of failures. The method is based on the stationary models set concept. As a formal description of TP CS life cycle is observed the machine graph for the flow of the three potential failures. It is concluded that TP CS design is a reconfiguration associated with the choice of measurement points to ensure the state observability, control actions induction points that satisfy the condition of control, and algorithm synthesis for decision-making.
Ключевые слова: отказоустойчивые системы управления, конечный автомат типа Мура, диагностика неисправностей, условия управления.
Keywords: technological process, control systems, fault-tolerance, failures, stationary models, decision-making, condition of control, machine graph.
Введение. Современные технологические процессы проектируются вместе со сложными системами управления иерархической структуры. Практика управления небезопасными технологическими установками, работающими вблизи критических режимов, делает актуальной проблему развития теории в направлении разработки моделей и методов расчета отказоустойчивых систем управления [1]. Следует также подчеркнуть, что основной контур управления и контур адаптации маскируют действия неисправностей, что затрудняет диагностирование последних. В статье рассматривается методика расчета систем управления ТП на основе конечного автомата типа Мура.
Разработанная методика базируется на изложенной в работах [1, 3] концепции множества стационарных моделей, в соответствии с которой действие неисправности, а также мероприятия по их ослаблению путем реконфигурирования основной системы интерпретируются как смена моделей. Отсюда следует принципиальная особенность моделей объектов управления техническим состоянием (ОУТС) СУ ТП. Она обусловлена тем, что имеется конечное множество технических состояний, элементами которого являются — исправная, неисправные и реконфигурированные (скорректированные, подстроенные для устранения неисправностей) системы. В случае множеств конечной мощности обращаемся к языку и методам дискретной математики, включая отношения на множествах, графы и комбинаторные алгоритмы.
Выходом управляемого объекта супервизорного уровня является техническое состояние СУ ТП, а входами — возмущения в виде системных неисправностей и управляющие воздействия в виде мер по реконфигурированию.
Уравнения, описывающие изменения технического состояния СУ ТП после первой по очереди неисправности, запишем так:
![]() (1)
(1)
· неисправная система является следствием действия неисправности ![]() на исправную систему
на исправную систему ![]() ;
;
![]() (2)
(2)
· после реконфигурирования ![]() получится скорректированная система. Предыдущая система получается сдвигом на шаг назад аргумента последующей системы, что обозначим знаком «минус» при нижнем индексе:
получится скорректированная система. Предыдущая система получается сдвигом на шаг назад аргумента последующей системы, что обозначим знаком «минус» при нижнем индексе: ![]() .
.
В уравнениях (1), (2) символ ![]() означает композицию систем. Системные неисправности
означает композицию систем. Системные неисправности ![]() и меры по их устранению
и меры по их устранению ![]() (так называемые мультипликативные взаимодействия) также рассматриваются как фрагменты систем.
(так называемые мультипликативные взаимодействия) также рассматриваются как фрагменты систем.
Структурная схема ОУТС (рис. 1) изображает ситуацию, когда случилась вторая по очереди неисправность. Приведем и систему уравнений для описания процессов после второй неисправности:
![]()
![]()
![]()
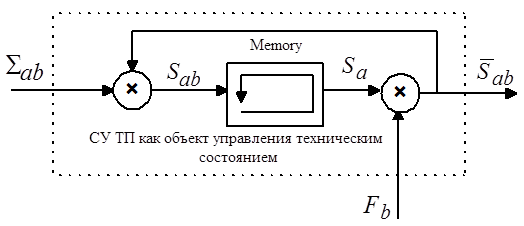
Рисунок 1. Структура объекта управления техническим состоянием (ОУТС)
На структурной схеме операцию сдвига потока событий выполняет элемент памяти Memory.
Объект управления техническим состоянием СУ ТП, как любой объект управления, имеет один выход — управляемую переменную и два выхода — возмущающее и управляющее воздействия. Предложенная структура относится к моделям типа «вход-состояние-выход», т. е. моделям в форме пространства состояний. Входами являются события в виде системных неисправностей ![]() и корректирующих действий
и корректирующих действий ![]() , выходом — событие
, выходом — событие ![]() , а состоянием — переменная
, а состоянием — переменная![]() .
.
Отметим, что предложенная модель оказывается статической, что является следствием игнорирования процессов перестройки СУ ТП. Темп процессов задает асинхронный поток неисправностей.
В том случае, когда имеет место последовательность (поток) неисправностей, для принятия решения о мерах ослабления их последствий необходимо управляющее устройство с памятью. Действительно, меры по реконфигурированию системы зависят не только от конкретной неисправности, но и от того, какова была предыдущая неисправность и каковой стала система после ее устранения. Для каждого из состояний, вообще говоря, необходима уникальная подсистема диагностирования, а для каждой неисправной системы может потребоваться свой механизм реконфигурирования.
Управляющее устройство, принимающее решение о реконфигурировании СУ ТП, реализует логический алгоритм, т. е. является дискретно-событийным устройством. На входе устройства сигнал имеет вид последовательности символов, отвечающих событиям в виде локализованных неисправностей (диагнозам), а на выходе — дискретные решения о конфигурировании СУ ТП.
Математическими моделями логических устройств с памятью являются конечные автоматы. Модель логического управляющего устройства (супервизора) представляет собой асинхронный автомат:
![]() ,
,
где: ![]() — входной алфавит — частично упорядоченное множество диагнозов;
— входной алфавит — частично упорядоченное множество диагнозов;
![]() — множество состояний автомата;
— множество состояний автомата;
![]() — начальное состояние, отвечающее исправной системе;
— начальное состояние, отвечающее исправной системе;
![]() — выходной алфавит — множество реконфигурирующих воздействий;
— выходной алфавит — множество реконфигурирующих воздействий;
![]() — функция переходов,
— функция переходов,
![]() — функция выходов.
— функция выходов.
Состояниям автомата отвечают системы: исправная, неисправные 1 раз, 2 раза и т. д., скорректированные 1 раз, 2 раза и т. д.
Выберем для определенности автомат типа Мура, выходы которого зависят только от состояния и не зависят напрямую от входа. Диаграмма графа автомата для потока из трех потенциальных неисправностей изображена на рис. 2. Вершинам графа типа «дерево» отвечают состояния и соответствующие им выходы, разделенные символом «/». Дугам графа соответствуют диагнозы о неисправностях.
Началу эксплуатации СУ ТП соответствует состояние ![]() , которое на диаграмме графа переходов-выходов будет обозначаться как 0.
, которое на диаграмме графа переходов-выходов будет обозначаться как 0.
Функционирование автомата после получения информации о первой неисправности опишем в форме следующих уравнений перехода состояний и выхода:

Выход ![]() — команда на реконфигурирование СУ ТП с неисправностью
— команда на реконфигурирование СУ ТП с неисправностью ![]() , выход
, выход ![]() — команда на перестройку подсистемы технической диагностики (нейросетевого классификатора) для диагностирования скорректированной СУ ТП.
— команда на перестройку подсистемы технической диагностики (нейросетевого классификатора) для диагностирования скорректированной СУ ТП.

Рисунок 2. Граф автомата типа Мура
Действия автомата после второй неисправности описываются так:

Аналогично можно записать уравнения автомата в случае последующей неисправности.
Супервизор рассчитан на поток неисправностей конечной длины. После того, как будет выявлена последняя неисправность, автомат переходит в конечное состояние ![]() . Дальнейшие решения требуют вмешательства обслуживающего персонала — СУ ТП необходимо вывести из эксплуатации для ремонта или утилизации.
. Дальнейшие решения требуют вмешательства обслуживающего персонала — СУ ТП необходимо вывести из эксплуатации для ремонта или утилизации.
Число состояний автомата — мощность множества ![]() — быстро (как говорят, комбинаторно) растет с увеличением числа потенциальных неисправностей
— быстро (как говорят, комбинаторно) растет с увеличением числа потенциальных неисправностей ![]() . Например, для
. Например, для ![]() число состояний автомата равно 3+3*2+3*2*1=15, что следует непосредственно из рис. 2.
число состояний автомата равно 3+3*2+3*2*1=15, что следует непосредственно из рис. 2.
Можно заметить, что автомат хранит в памяти «историю болезни» СУ ТП — каждое его состояние соответствует одной из систем, а единственный путь от вершины 0 до определенной вершины дает информацию о конкретном потоке неисправностей и мер, принятых по ослаблению их воздействия. После заданного числа неисправностей принимается решение о выводе СУ ТП из эксплуатации для ремонта или утилизации.
Заключение. Граф автомата (рис. 2) можно интерпретировать как формальное описание жизненного цикла СУ ТП. Более того, в этот цикл можно включить и этап проектирования, если за начальное состояние принять технологический процесс, динамика которого нас не устраивает. Тогда проектирование СУ ТП представляет собой реконфигурирование, связанное с выбором точек измерения, обеспечивающих наблюдаемость состояний, точек введения управляющих воздействий, которые удовлетворяют условию управляемости, и синтезом алгоритма принятия решений.
Список литературы:
1.Имаев Д.Х., Шестопалов М.Ю. Системы, толерантные к неисправностям — инновационное направление в управлении сложными процессами // Инновации. 2012. № 7 (165). С. 109—112.
2.Имаев Д.Х., Шестопалов М.Ю. Топологические и матричные условия локализации неисправностей систем управления // Известия СПбГЭТУ «ЛЭТИ». 2012. № 5. С. 36—44
3.Шевцов И.В., Шестопалов М.Ю. Модели управления и диагностики технологического процесса производства никелевого порошка. СПб.: Изд-во СПбГЭТУ «ЛЭТИ». 2012. 218 с.
дипломов


Оставить комментарий