Статья опубликована в рамках: XXV Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 04 сентября 2013 г.)
Наука: Технические науки
Секция: Информатика, вычислительная техника и управление
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
СЕГМЕНТАЦИЯ ПОСЛЕДОВАТЕЛЬНОСТЕЙ ИЗОБРАЖЕНИЙ С РЕГУЛИРУЕМОЙ ТОЧНОСТЬЮ И ВИЗУАЛИЗАЦИЯ ЭФФЕКТИВНОСТИ
Кузьмин Сергей Александрович
старший преподаватель, СПбГУАП, Санкт-Петербург
E-mail:
SEGMENTATION OF IMAGE SEQUENCES WITH CONTROLLED ACCURACY AND VISUALISATION OF PERFORMANCE
Kuzmin Sergey Alexandrovich
teaching fellow, SPb SUAI, Saint-Petersburg
АННОТАЦИЯ
Для снижения вычислительной сложности анализа изображений большой площади стараются сначала найти интересующие объекты на низком разрешении, а затем уже рассмотреть их на более высоком разрешении. Описывается семейство алгоритмов сегментации изображений с движущимися объектами и методики визуализации эффективности алгоритмов сегментации и шумоподавления.
ABSTRACT
For reduction of the computational complexity of image analysis with large area it is common practice at first to find objects at a low resolution, and then to gaze them at a higher resolution. This article is devoted to a family of algorithms for segmentation of images and techniques for visualization of effectiveness of segmentation and noise reduction algorithms.
Ключевые слова: вейвлет преобразование, сегментация, пирамида изображений, фильтрация изображений, ROC характеристика.
Keywords: wavelet transform, segmentation, image pyramid, image filtering, ROC curve.
Семейство алгоритмов сегментации с различной точностью
В 2006, 2007 и 2013 годах были разработаны идейно близкие способы локализации объектов с пониженной [5], нормальной [3] и повышенной (субпиксельной) точностью. Основная идея заключается в объединении изменяющихся участков кадра («движущихся областей») и смещающихся контуров объектов («движущихся контуров») с помощью операции «ИЛИ».
Изменение пространственной точности определения координат объектов связано с вычислением нужного уровня пирамиды разрешений. В отличие от наиболее часто рассматриваемых способов построения пирамиды, направленных только на снижение разрешения, в статье рассматривается и способ увеличения разрешения изображения.
Первый разработанный алгоритм представлен на рис. 1.

Рисунок 1. Блок-схема алгоритма сегментации, основанного на разнице «нулевых» уровней вейвлет-преобразований
В нём нет изменения площади яркостной составляющей кадра, поэтому можно говорить, что он связан с «нулевым уровнем» вейвлет-преобразования: ![]() . Вейвлет-преобразование имитируется путем вычисления контуров фильтром Превитт. Разностные кадры бинаризуются и объединяются с помощью операции «ИЛИ».
. Вейвлет-преобразование имитируется путем вычисления контуров фильтром Превитт. Разностные кадры бинаризуются и объединяются с помощью операции «ИЛИ».
Традиционное направление связано с понижением разрешения изображения. Ранее это было актуально из-за низкой скорости вычислений даже на небольших изображениях. Сейчас размеры изображений стремительно растут, а также в СПБГУАП активно развивается направление видеопанорам, поэтому скорость вычислений по-прежнему является больной точкой и понижение разрешения актуально в случае обработки изображений больших площадей. В теории рассматриваются разные способы вычисления сглаженной и прореженной версии изображения (Гауссиан [10], фильтр Габора [9], среднее, минимальное или максимальное значение, полусумма минимального и максимального значений, медиана участка изображения предыдущего уровня пирамиды[1], морфологическая операция «размыкание» (чередование базовых операций «эрозия» и «наращивание»), вейвлет преобразование [8]). В данной работе используются вейвлеты.
Второй разработанный алгоритм основан на настоящем вейвлет преобразовании. На основании исследований [7] для вычисления низкочастотной (НЧ) и высокочастотных (ВЧ) составляющих был выбран вейвлет Хаара. После прямого двумерного дискретного вейвлет преобразования (ДВП) изображения кадра три высокочастотных диапазона, соответствующих изменениям в горизонтальном, вертикальном и диагональном направлениях, объединяются суммированием амплитуд трансформант с проверкой переполнения разрядной сетки:
![]() .
.
Аналогичные операции производятся для изображения оценки фона. Затем следует попарное вычисление разниц НЧ и объединенных ВЧ составляющих (рис. 2). Объединение бинаризованных разностных изображений производится также с помощью операции «ИЛИ».
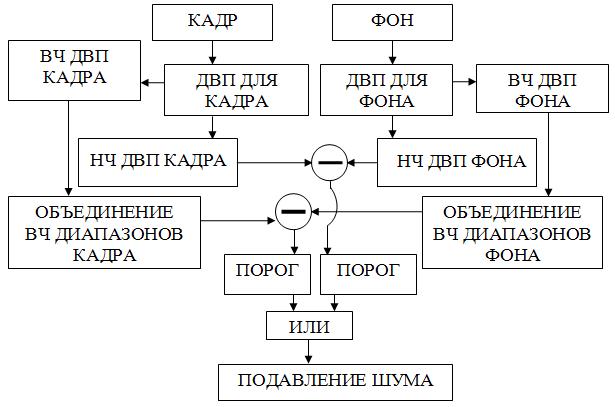
Рисунок 2. Блок-схема алгоритма сегментации, основанного на разнице первых «отрицательных» уровней вейвлет преобразований
Размеры получаемых изображений в 4 раза меньше, чем исходных, то есть можно сказать, что речь идет о первом отрицательном уровне разложения: ![]() . Более глубокие «отрицательные уровни» разложения получаются применением вейвлет преобразования к НЧ составляющей ДВП, а затем осуществлением объединения ВЧ диапазонов.
. Более глубокие «отрицательные уровни» разложения получаются применением вейвлет преобразования к НЧ составляющей ДВП, а затем осуществлением объединения ВЧ диапазонов.
Если требуется точность определения координат объектов меньше пикселя, то необходимо задуматься о реализации «положительных уровней» разложения, т. е. повышении площади яркостной составляющей изображения (рис. 3). Первые работы в направлении повышения разрешения изображений с помощью вейвлет-преобразования были сделаны в начале 2000-х годов [11].

Рисунок 3. Блок-схема алгоритма обнаружения, основанного на разнице первых «положительных» уровней вейвлет преобразований
Размеры получаемых изображений в 4 раза больше, чем исходных, то есть можно сказать, что речь идет о первом положительном уровне разложения: ![]() (такие обозначения введены из-за специфики процесса вычисления двумерного вейвлет-преобразования, каждый уровень которого выполняется в два этапа — сначала по горизонтали, а затем по вертикали). Следующие «положительные уровни» получаются тем же способом — вычисление контуров изображения в трех направлениях, выполнение обратного вейвлет преобразования.
(такие обозначения введены из-за специфики процесса вычисления двумерного вейвлет-преобразования, каждый уровень которого выполняется в два этапа — сначала по горизонтали, а затем по вертикали). Следующие «положительные уровни» получаются тем же способом — вычисление контуров изображения в трех направлениях, выполнение обратного вейвлет преобразования.
Различие между алгоритмами семейства в спектральной области приводит к отличающимся характеристикам их эффективности. При вычислении отрицательных уровней контуры сильно ослабляются, что приводит к потере высокочастотной энергии. При вычислении положительных уровней контуры растягиваются в пространстве, что снижает их крутизну и сдвигает высокие частоты в область средних частот. Поэтому по наличию высокочастотной энергии, критически важной для выделения «движущихся контуров», можно априорно расположить эффективность алгоритмов разных уровней в следующем порядке: нулевой, положительные, отрицательные. Это подтверждается результатами эксперимента (рис. 4).

Рисунок 4. Графики ![]() для разных уровней семейства алгоритмов. Методы сегментации: зеленый — нулевой уровень, красный — плюс первый, синий — минус первый.
для разных уровней семейства алгоритмов. Методы сегментации: зеленый — нулевой уровень, красный — плюс первый, синий — минус первый.
Визуализация эффективности движения к требуемым показателям точности
Разработчику заданы минимально приемлимые значения вероятностей правильного обнаружения Рпо и ложной тревоги Рпо, по которым можно построить минимально приемлемую целевую характеристику Рпо = f(Рпо). Рассмотрим понятие зона требуемой точности — это область в верхнем левом углу характеристики Рпо = f(Рлт), ограниченная требуемыми значениями Рпо и Рлт, в которой должна находиться хотя бы одна точка целевой характеристики. Для примера на рис. 5 показана зона требуемой точности в виде квадрата (1), одна из целевых характеристик (2) и характеристика алгоритма сегментации (3).
Как правило, характеристика алгоритма сегментации сильно отличается от целевой характеристики. Конкретная точка на характеристике, соответствующая определенному соотношению белых и черных пикселей, выбирается критерием. Соответственно на начальном этапе выбранная критерием рабочая точка находится далеко от зоны требуемой точности. Тогда возникает желание скачком переместиться поближе к этой зоне. Для реализации такого скачка часто используют объединение двух и более алгоритмов сегментации.

Рисунок 5 Пояснение к построению зоны требуемой точности и одной из целевых характеристик Рпо=f(Рлт).
После объединения изображений — результатов работы алгоритмов сегментации — получается изображение с определенными мощностями множеств черных и белых пикселей. Эти мощности определяют значения показателей Рпо, Рлт, то есть точку в пространстве характеристики Рпо=f(Рлт). Через эту точки проходит зависимость Рпо=f(Рлт) объединенного алгоритма. Если полученная точка всё еще далека от зоны требуемой точности, то полученное бинарное изображение можно объединять еще с каким-то алгоритмом сегментации или применять к нему фильтры. Это приведет к появлению еще одной точки в пространстве Рпо=f(Рлт). Эти точки, получаемые после каждого блока обработки, можно отобразить в виде графика рабочих точек (рис. 6). Таким образом, в процессе создания алгоритма анализа видеоинформации разработчик реализует одну из траекторий движения к зоне требуемой точности, создавая набор смещающихся характеристик Рпо=f(Рлт).

Рисунок 6. График рабочих точек в пространстве характеристики Рпо=f(Рлт) для алгоритма «нулевого уровня». Цифрами обозначены рабочие точки после этапов обработки изображения.
Особенностью разработанного семейства алгоритмов сегментации являются необычная траектория движения к целевым показателям (целевой характеристике), получающая после объединения алгоритмов с помощью операции «ИЛИ». Нестандартной она является, т. к. наиболее распространены подходы объединения с помощью операции «И» или построенные на определенных правилах.
Алгоритмы сегментации, построенные на операции «ИЛИ», в результате объединения получают высокую вероятность ложных тревог и высокую вероятность правильного обнаружения. Таким образом, разработчик, реализующий операцию «ИЛИ» должен разработать алгоритмы подавления шумов, чтобы приблизиться к зоне требуемой точности.
Визуализация эффективности подавления шума
Объединение результатов работы алгоритмов сегментации с помощью операции «ИЛИ» мало исследовано в связи с возникающими трудностями из-за возрастающей вероятности повреждения изображения. В [4] были приведены сведения о фильтрах, позволяющих значительно снизить вероятность повреждения изображения в блоках подавления шума. К фильтрам подавления шума относится многошаговый медианный фильтр (см. [2, с. 124—125]).
Для иллюстрации эффективности фильтрации изображений в [6] предложен способ визуализации «гистограмма связности». Каждый пиксель растрового изображения имеет вокруг себя некоторое количество других пикселей — множество, называемое окрестностью этого пикселя. Обозначим символом С количество анализируемых пикселей, окружающих пиксель I[x,y], т. е. количество проверяемых связей. Пиксель изображения считается «связанным» с соседним пикселем, принадлежащим окрестности, если их яркости одинаковы. Обозначим количество соседей пикселя символом U[x,y]. Обозначим количество пикселей изображения, имеющих одинаковую связность, символом WU, где U![]() [0..С].
[0..С].
Понятия, характеризующие изображение:
1. гистограмма связности изображения (области) — это гистограмма, в которой отражается статистика области ![]() , где
, где ![]() — площадь изображения. Под выделенными пикселями понимаются пиксели того цвета, который в данный момент представляет интерес (как правило, белый в бинарных изображениях);
— площадь изображения. Под выделенными пикселями понимаются пиксели того цвета, который в данный момент представляет интерес (как правило, белый в бинарных изображениях);
2. общее количество соседей у всех выделенных пикселей — это величина  , где
, где ![]() — количество связей у выделенного пикселя;
— количество связей у выделенного пикселя;
3. средняя связность изображения — это величина ![]() , где
, где ![]() — общее количество выделенных пикселей.
— общее количество выделенных пикселей.
Примеры построения гистограмм связности приведены на рис. 7—9.

Рисунок 7. Исходное бинарное изображение и его гистограмма связности. Средняя связность равна 5,3746

Рисунок 8. Изображение после многошаговой медианной фильтрации и его гистограмма связности. Средняя связность равна 6,0646

Рисунок 9. Изображение после медианной фильтрации и его гистограмма связности. Средняя связность равна 6,8496
Импульсы шума представляют из себя одиночные резкие скачки яркости. В результате у зашумленного изображения средняя связность низкая. В ходе обработки фильтрами на основе порядковой статистики связность повышается за счет подавления одиночных импульсов.
Заключение
По проведенным исследованиям сделаны следующие выводы:
1. к семейству алгоритмов с регулируемой точностью сегментации добавлены положительные уровни, что позволяет определять положение объектов с субпиксельной точностью;
2. наибольшая точность у алгоритмов «нулевого уровня»;
3. разработана методика визуализации эффективности различных этапов в процессе сегментации изображений;
4. на основе методики визуализации «гистограмма связности» установлено, что классический медианный фильтр эффективнее многошагового медианного фильтра в подавлении импульсного шума.
Список литературы:
1.Александров В.В., Горский Н.Д. Представление и обработка изображений. Рекурсивный подход. Л.: Наука, 1985. — 192 с.
2.Егорова С.Д., Колесник В.А. Оптико-электронное цифровое преобразование изображений. М.: Радио и связь, 1991. — 208 с.
3.Кузьмин С.А. Обнаружение движущихся визуальных объектов на основе выделения областей и контуров, не принадлежащих фону// Молодые ученые — промышленности Северо-Западного региона: Материалы конференций политехнического симпозиума. Декабрь 2006 года. СПб.: Изд-во Политехн. ун-та, 2006. — С. 56.
4.Кузьмин С.А. Исследование комбинации детектора импульсного шума в бинарных изображениях и процентильных фильтров// «Естественные и математические науки в современном мире»: материалы IX международной заочной научно-практической конференции. (19 августа 2013 г.) Новосибирск: Изд. «СибАК», 2013. — C. 34—44.
5.Кузьмин С.А. Обнаружение визуальных объектов с использованием вейвлет-преобразования и оценивания фона//Системы управления и информационные технологии, 2.1(28), 2007. — С. 158—162.
6.Кузьмин С.А. Повышение вероятности правильного обнаружения объектов в видеопоследовательности с помощью ранговых операторов// Научная сессия ГУАП: Сб. докл.: В 3 ч. Ч. II. Технические науки /СПбГУАП. СПб., 2010. — С. 41—44.
7.Кузьмин С.А. Исследование точности сегментации подвижных объектов с использованием вейвлетов семейства Добеши// Научная сессия ГУАП: Сб. докл.: В 3 ч. Ч. II. Технические науки /СПбГУАП. СПб., 2008. — С. 32—35.
8.Харатишвили Н.Г., Чхеидзе И.М. Морфологические построения в кодировании изображений. Тбилиси: Грузинский технический университет, 2009. — 144 с.
9.Чочиа П.А. Пирамидальный алгоритм сегментации изображений // Информационные процессы, — Том 10, — № 1, — 2010. — С. 23—35.
10.Burt P.J. and Adelson E.H., The Laplacian pyramid as a compact image code, IEEE Trans. Commun., — vol. 31, — № 4, — pp. 532—540, — April 1983.
11.Shcherbakov M.A., Schegolev W.Y. A Wavelet-based Technique for Image Refinement, EUSIPCO-2000, Tampere, pp. 1737—1739.
дипломов


Оставить комментарий