Статья опубликована в рамках: XXX Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 22 января 2014 г.)
Наука: Технические науки
Секция: Электротехника
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
ОПРЕДЕЛЕНИЕ МОЩНОСТИ ГАРМОНИЧЕСКОГО ТОКА В КОМПЛЕКСНОЙ ФОРМЕ
Копылов Алексей Филиппович
канд. техн. наук, доцент кафедры Радиотехника Института инженерной физики и радиоэлектроники Сибирского федерального университета, РФ, г. Красноярск
E-mail: kopaph@yandex.ru
Копылова Наталья Алексеевна
инженер-программист Межшкольного методического Центра Октябрьского района, РФ, г. Красноярск
POWER DEFINITION HARMONIC CURRENT IN THE COMPLEX FORM
Alexei Kopylov
candidate of Technical Sciences, Associate Professor of Radio Technical Department of Physicists and Radio Technicians Engineering of Siberian Federal University, Russia Krasnoyarsk
Natalia Kopylova
part-programming engineer Methodological centre of October district, Russia Krasnoyarsk
АННОТАЦИЯ
В работе приведен подробный вывод выражений для определения мощности гармонического тока в случае, когда ток и напряжение цепи выражены в форме комплексных амплитуд. Показано, какие сочетания комплексных амплитуд токов и напряжений, а также комплексно сопряженных с ними величин, соответствуют активной и реактивной мощностям гармонического тока. Вывод может быть полезен при подробном изучении дисциплин по электро- и радиотехнике.
ABSTRACT
The paper provides a detailed derivation of the expressions for determining the power of the harmonic current in the case where the current and the voltage are expressed in the form of complex amplitudes. Shows which combinations of the complex amplitudes of the currents and voltages, as well as complex conjugate with them values correspond to active and reactive power harmonic current. The derivation of mathematical expressions can be useful for a detailed study of disciplines on electrical engineering.
Ключевые слова: ток; напряжение; мощность в комплексной форме.
Keywords: current; voltage; power in complex form.
Как показывает опыт обучения студентов по дисциплинам, связанным с электро- и радиотехникой, определенные проблемы в учебном процессе возникают при изучении темы расчета мощности гармонического тока в комплексной форме. Даже у квалифицированного читателя при изучении этого материала возникает вопрос о строгости в получении выражений, описывающих мощность гармонического тока в комплексной форме. При ближайшем рассмотрении оказывается, что этот вопрос возникает не случайно. В самом деле, при подробном рассмотрении оказывается, что получение строгого решения для комплексной мощности обходят стороной как авторы современных учебников и учебных пособий [1—3], так и основоположники теории электрических цепей и электротехники [4]. Во всех этих источниках [1—4], в тех или иных модификациях приводится результирующая формула для определения мощности гармонического тока в комплексной форме ![]() через комплексные амплитуды тока в цепи
через комплексные амплитуды тока в цепи ![]() и напряжения на ней
и напряжения на ней ![]() и комплексно сопряженные с ними величины
и комплексно сопряженные с ними величины ![]() и
и ![]() :
:
 , (1)
, (1)
где: ![]() — комплексная мощность в цепи гармонического тока, ВА;
— комплексная мощность в цепи гармонического тока, ВА;
![]() — активная мощность в цепи гармонического тока, Вт;
— активная мощность в цепи гармонического тока, Вт;
![]() — реактивная мощность в цепи гармонического тока, вар;
— реактивная мощность в цепи гармонического тока, вар;
j — мнимая единица,
![]() и
и ![]() — комплексная амплитуда и сопряженная с ней величина тока в цепи (ветви схемы), для которой определяется мощность, А;
— комплексная амплитуда и сопряженная с ней величина тока в цепи (ветви схемы), для которой определяется мощность, А;
![]() и
и ![]() — комплексная амплитуда и сопряженная с ней величина падения напряжения на цепи (ветви схемы), для которой определяется мощность, В;
— комплексная амплитуда и сопряженная с ней величина падения напряжения на цепи (ветви схемы), для которой определяется мощность, В;
![]() — величина, комплексно сопряженная с действующим значением комплексной амплитуды тока цепи (ветви схемы), для которой определяется мощность, А;
— величина, комплексно сопряженная с действующим значением комплексной амплитуды тока цепи (ветви схемы), для которой определяется мощность, А;
![]() — действующее значение комплексной амплитуды падения напряжения на цепи (ветви схемы), для которой определяется мощность, В.
— действующее значение комплексной амплитуды падения напряжения на цепи (ветви схемы), для которой определяется мощность, В.
Осуществим подробный вывод выражения (1). Для этого положим мгновенное значение тока ![]() в цепи в виде гармонической функции с нулевой начальной фазой:
в цепи в виде гармонической функции с нулевой начальной фазой:
![]() , (2)
, (2)
где: ![]() — мгновенное значение тока в цепи, А;
— мгновенное значение тока в цепи, А;
![]() — амплитудное значение тока в цепи, А;
— амплитудное значение тока в цепи, А;
![]() — круговая частота, рад/с;
— круговая частота, рад/с;
![]() — текущее значение времени, с.
— текущее значение времени, с.
Поскольку ток и напряжение в цепи гармонического тока в общем случае не совпадают по фазе, мгновенное значение напряжения ![]() на цепи положим также в виде гармонической функции, но с ненулевой начальной фазой
на цепи положим также в виде гармонической функции, но с ненулевой начальной фазой ![]() :
:
![]() , (3)
, (3)
где: ![]() — мгновенное значение напряжения на цепи, В;
— мгновенное значение напряжения на цепи, В;
![]() — амплитудное значение напряжения на цепи, В;
— амплитудное значение напряжения на цепи, В;
![]() — начальная фаза напряжения на цепи, рад.
— начальная фаза напряжения на цепи, рад.
Мгновенное значение мощности гармонического тока ![]() при этом будет равно произведению мгновенного значения тока
при этом будет равно произведению мгновенного значения тока ![]() в цепи, выражение (2), на мгновенное значение напряжения
в цепи, выражение (2), на мгновенное значение напряжения ![]() на цепи, выражение (3):
на цепи, выражение (3):
![]() . (4)
. (4)
Или в виде, содержащем сумму мгновенной поглощаемой мощности ![]() и мгновенной поступающей на реактивные элементы мощности
и мгновенной поступающей на реактивные элементы мощности ![]() :
:
 , (5)
, (5)
где: ![]() — мгновенная поглощаемая в цепи мощность, Вт;
— мгновенная поглощаемая в цепи мощность, Вт;
![]() — мгновенная поступающая на реактивные элементы цепи мощность, вар;
— мгновенная поступающая на реактивные элементы цепи мощность, вар;
![]() — значение активной мощности в цепи, Вт;
— значение активной мощности в цепи, Вт;
![]() — значение реактивной мощности в цепи, вар.
— значение реактивной мощности в цепи, вар.
Полного эквивалента выражению (5) в комплексной форме подобрать не удается из-за неполного соответствия комплексных изображений исходным гармоническим функциям. Такое несоответствие возникает, когда появляется необходимость физической интерпретации комплексных операторов вращения вида ![]() и
и ![]() , появляющихся при преобразованиях синусоидальных функций времени тока, напряжения и мощности. В частности, при изображении гармонических множителей в выражении (5), оператор вращения
, появляющихся при преобразованиях синусоидальных функций времени тока, напряжения и мощности. В частности, при изображении гармонических множителей в выражении (5), оператор вращения ![]() может изображать как синусоидальный множитель
может изображать как синусоидальный множитель ![]() , так и косинусоидальный множитель
, так и косинусоидальный множитель ![]() . Это приводит к неоднозначности изображения исходных гармонических функций в области комплексной переменной. По этой причине при преобразовании функций времени (5) в комплексную форму приходится опускать гармонические множители и преобразовывать только активную
. Это приводит к неоднозначности изображения исходных гармонических функций в области комплексной переменной. По этой причине при преобразовании функций времени (5) в комплексную форму приходится опускать гармонические множители и преобразовывать только активную ![]() и реактивную
и реактивную ![]() мощности.
мощности.
Преобразование активной составляющей ![]() комплексной мощности
комплексной мощности ![]() цепи гармонического тока дает четыре возможных варианта выражений для активной мощности через комплексные и сопряженные с ними токи и напряжения:
цепи гармонического тока дает четыре возможных варианта выражений для активной мощности через комплексные и сопряженные с ними токи и напряжения:
 ;
; 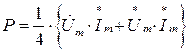 ;
;
 ;
;  . (6)
. (6)
В результате подстановки в каждое из выражений (6) величин ![]() ,
, ![]() ,
, ![]() и
и ![]() , выраженных через их реальные и мнимые составляющие, получается:
, выраженных через их реальные и мнимые составляющие, получается:
 , (7)
, (7)
 , (8)
, (8)
 , (9)
, (9)
 , (10)
, (10)
где: ![]() ,
, ![]() — действительная и мнимая части комплексной амплитуды тока цепи (ветви);
— действительная и мнимая части комплексной амплитуды тока цепи (ветви);
![]() ,
, ![]() — действительная и мнимая части комплексной амплитуды напряжения на цепи (на ветви), для которой определяется мощность.
— действительная и мнимая части комплексной амплитуды напряжения на цепи (на ветви), для которой определяется мощность.
Первое (7) и второе (8) уравнения этой системы не могут быть выражениями для нахождения активной мощности ![]() в цепи гармонического тока, так как в составе этих выражений есть мнимая составляющая. Третье (9) уравнение системы допускает получение отрицательной мощности, не обусловленной несовпадением направлений тока и напряжения в цепи (ветви):
в цепи гармонического тока, так как в составе этих выражений есть мнимая составляющая. Третье (9) уравнение системы допускает получение отрицательной мощности, не обусловленной несовпадением направлений тока и напряжения в цепи (ветви): ![]() . Всем физическим соображениям для выражения активной мощности
. Всем физическим соображениям для выражения активной мощности ![]() соответствует только четвертое (10) уравнение: это уравнение не содержит мнимых составляющих, и не содержит элементов, допускающих появления отрицательной мощности, не обусловленной несовпадением направлений тока и напряжения в цепи (ветви).
соответствует только четвертое (10) уравнение: это уравнение не содержит мнимых составляющих, и не содержит элементов, допускающих появления отрицательной мощности, не обусловленной несовпадением направлений тока и напряжения в цепи (ветви).
Аналогичное выполненному выше (6), преобразование можно осуществить для реактивной составляющей ![]() комплексной мощности
комплексной мощности ![]() . Преобразование реактивной составляющей
. Преобразование реактивной составляющей ![]() комплексной мощности
комплексной мощности ![]() цепи гармонического тока также дает четыре возможных варианта выражений для реактивной мощности через комплексные и сопряженные с ними токи и напряжения:
цепи гармонического тока также дает четыре возможных варианта выражений для реактивной мощности через комплексные и сопряженные с ними токи и напряжения:
 ;
; ;
;
 ;
; . (11)
. (11)
В результате подстановки в каждое из выражений (11) величин ![]() ,
, ![]() ,
, ![]() и
и ![]() , выраженных через их реальные и мнимые составляющие, получим:
, выраженных через их реальные и мнимые составляющие, получим:
 , (12)
, (12)
 , (13)
, (13)
 , (14)
, (14)
 . (15)
. (15)
Проанализируем уравнения (12)—(15), полученные для реактивной мощности ![]() в комплексной форме, с точки зрения физического смысла. Уравнения (12) и (13) не могут выражать реактивную мощность, так как они содержат, наряду с реактивными, и активные составляющие, а это физически невозможно. Выражение (14), хотя и не содержит действительных составляющих, как это было ранее в выражениях (12) и (13), и, на первый взгляд, может выражать реактивную мощность
в комплексной форме, с точки зрения физического смысла. Уравнения (12) и (13) не могут выражать реактивную мощность, так как они содержат, наряду с реактивными, и активные составляющие, а это физически невозможно. Выражение (14), хотя и не содержит действительных составляющих, как это было ранее в выражениях (12) и (13), и, на первый взгляд, может выражать реактивную мощность ![]() , также не подходит на эту роль. Уравнение (14) не позволяет реактивной мощности принимать отрицательные значения, а это неизбежно случится при изменении реактивного характера сопротивления цепи с активно-индуктивного на ёмкостно-индуктивный. Всем критериям выражения, которое может определять реактивную мощность
, также не подходит на эту роль. Уравнение (14) не позволяет реактивной мощности принимать отрицательные значения, а это неизбежно случится при изменении реактивного характера сопротивления цепи с активно-индуктивного на ёмкостно-индуктивный. Всем критериям выражения, которое может определять реактивную мощность ![]() , соответствует последнее уравнение (15): оно содержит только реактивные составляющие и может иметь различные знаки в зависимости от характера реактивности сопротивления цепи.
, соответствует последнее уравнение (15): оно содержит только реактивные составляющие и может иметь различные знаки в зависимости от характера реактивности сопротивления цепи.
Таким образом, в результате подбора выражения для изображения активной мощности ![]() из возможных вариантов (7)—(10), удовлетворяющим физическому смыслу этой мощности оказывается изображение (10), а для изображения реактивной мощности
из возможных вариантов (7)—(10), удовлетворяющим физическому смыслу этой мощности оказывается изображение (10), а для изображения реактивной мощности ![]() из возможных вариантов (12)—(15) удовлетворяющим физическому смыслу этой мощности оказывается выражение (15). Комплексная мощность
из возможных вариантов (12)—(15) удовлетворяющим физическому смыслу этой мощности оказывается выражение (15). Комплексная мощность ![]() цепи гармонического тока при этом будет определяться выражением:
цепи гармонического тока при этом будет определяться выражением:
 . (16)
. (16)
Полученные в настоящей работе выражения для комплексной мощности ![]() цепи гармонического тока (16), её активной
цепи гармонического тока (16), её активной ![]() (10) и реактивной
(10) и реактивной ![]() (15) составляющих, полностью совпадают с имеющимися в литературе [1—4] результатами (1). Весь показанный в настоящей работе процесс вывода соотношения (1) показывает, что это соотношение не имеет физического смысла, а является чисто формальным и позволяет использовать его только для практических расчетов и не может быть использовано для каких-либо физических интерпретаций с понятиями мощности, используемыми в электро- и радиотехнике.
(15) составляющих, полностью совпадают с имеющимися в литературе [1—4] результатами (1). Весь показанный в настоящей работе процесс вывода соотношения (1) показывает, что это соотношение не имеет физического смысла, а является чисто формальным и позволяет использовать его только для практических расчетов и не может быть использовано для каких-либо физических интерпретаций с понятиями мощности, используемыми в электро- и радиотехнике.
Список литературы:
1.Основы теории цепей [Текст]: учебник / Г.И. Атабеков. 2-е изд., испр. СПб.: Лань, 2006. — 424 с. — ISBN 5-8114-0699-1 (в пер).
2.Основы теории цепей [Текст]: учебник для электротехн. и электроэнерг. спец. вузов / Г.В. Зевеке, П.А. Ионкин, А.В. Нетушил, С.В. Страхов. 5-е изд., перераб. М.: Энергоатомиздат, 1989. — 528 с.: ил. — ISBN 5-283-00523-2 (в пер).
3.Основы теории цепей [Текст]: Учебник для студентов вузов / В.П. Попов. 6-е изд., испр. М.: Высшая школа, 2007. — 575 с.: ил. — ISBN 978-5-06-003949-8 (в пер).
4.Основы электротехники / К.А. Круг. 4-е изд., перераб. Утв. Комитетом по высшему техническому образованию при ЦИК СССР в качестве основного учебного руководства для энергетических втузов. Объединенное научно-техническое изд-во глав. ред. энергетической литературы, 1936. — 888 с.: ил.
дипломов


Оставить комментарий