Статья опубликована в рамках: XXXI Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 26 февраля 2014 г.)
Наука: Технические науки
Секция: Аэрокосмическая техника и технологии
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
ОБ УРАВНЕНИЯХ В ВАРИАЦИЯХ В ЗАДАЧЕ О ДВИЖЕНИИ ТОЧКИ В ВОЗМУЩЕННОМ ЦЕНТРАЛЬНОМ ПОЛЕ
Бабаджанянц Левон Константинович
д-р физ.-мат. наук, профессор Санкт-Петербургского государственного университета, РФ, г. Санкт-Петербург
E -mail: levon@mail.wplus.net
Брэгман Анна Михайловна
студент Санкт-Петербургского государственного университета, РФ, г. Санкт-Петербург
E -mail: meune@mail.ru
Брэгман Константин Михайлович
старший преподаватель Санкт-Петербургского государственного университета, РФ, г. Санкт-Петербург
E -mail: beswdw@gmail.com
Касикова Полина Владимировна
системный администратор, Управление-Служба информационных технологий Санкт-Петербургского государственного университета, РФ, г. Санкт -Петербург
E-mail:
ON EQUATIONS IN VARIATIONS TO THE PROBLEM OF MOTION OF A POINT MASS IN PERTURBED CENTRAL FORCE FIELD
Levon Babadzanjanz
doctor of Science, professor of Saint-Petersburg State University, Russia Saint-Peretsburg
Anna Bregman
student of Saint-Petersburg State University, Russia Saint-Peretsburg
Konstantin Bregman
senior Lecturer of Saint-Petersburg State University, Russia Saint-Peretsburg
Polina Kasikova
administration-Service of Information Technologies of Saint-Petersburg State University, system administrator, Russia Saint-Peretsburg
АННОТАЦИЯ
Решение уравнений в вариациях для задачи о движении материальной точки в произвольном центральном n-мерном силовом поле с возмущением сводится к последовательному рассмотрению n линейных однородных дифференциальных уравнений второго порядка, что существенно упрощает решение и соответствующих неоднородных уравнений, а значит и реализацию метода малого параметра при построении моделей движения тел в различных силовых полях.
ABSTRACT
The process of solution of equations of variations for the problem of motion of a point mass in a perturbed central force field we reduce to the consideration of n second order homogeneous linear equations. Because of this, the process of solution of corresponding inhomogeneous equations becomes easy enough, and it implies that construction of models of motion of bodies under the action of various forces (when using the small parameters methods) becomes easier too.
Ключевые слова : уравнение в вариациях; центральное поле; уравнения дви-жения.
Keywords: equations of variations; central force field; equations of motion.
Рассмотрим движение материальной точки ![]() массы
массы ![]() в центральном поле сил
в центральном поле сил ![]() относительно репера
относительно репера ![]() в аффинном евклидовом пространстве
в аффинном евклидовом пространстве ![]() . Движение этой точки при наличии возмущений удовлетворяет уравнениям Ньютона
. Движение этой точки при наличии возмущений удовлетворяет уравнениям Ньютона
![]() ,
,
![]() ,
, ![]() ,
,![]() ,
,![]() ,
,
которые запишем в виде:
![]() ,
,![]() . (1)
. (1)
Зададим начальные условия:
![]() (или
(или ![]() ), (2)
), (2)
а решение задачи Коши (1), (2) обозначим ![]() . Рассмотрим также невозмущенные уравнения
. Рассмотрим также невозмущенные уравнения
![]() (или
(или ![]() ) (3)
) (3)
и начальные условия
![]() (или
(или ![]() ). (4)
). (4)
Вычитая уравнения (3) из уравнений (1), для возмущений ![]()
(или ![]() ) получаем :
) получаем :
![]()
В первом приближении имеем:

где ![]() ,
, ![]() .
.
Если возмущения ![]() считаются малыми по сравнению с
считаются малыми по сравнению с ![]() , а начальные данные в (4) выбраны так, что
, а начальные данные в (4) выбраны так, что ![]() можно считать приемлемым начальным приближением для решения задачи Коши (1), (2), то полученные уравнения (первого приближения)
можно считать приемлемым начальным приближением для решения задачи Коши (1), (2), то полученные уравнения (первого приближения)
 (5)
(5)
называют уравнениями теории первого порядка относительно возмущений ![]() [3]. Отметим, что величина
[3]. Отметим, что величина ![]() отличается от
отличается от ![]() на величину второго порядка по возмущениям
на величину второго порядка по возмущениям ![]() .
.
Решение уравнений (5) связано с большими сложностями, хотя фундаментальная матрица принципиально может быть найдена согласно теореме Пуанкаре о том, что ее столбцы составлены из производных невозмущенных координат по независимым произвольным постоянным (входящим в общее решение невозмущенных уравнений). Но особенно сложным является переход от решения однородной системы (5) к неоднородной, так как придется интегрировать дроби в числителе которых стоят определители ![]() порядка, а в знаменателе определитель
порядка, а в знаменателе определитель ![]() порядка, элементы которых сложным образом зависят от элементов фундаментальной матрицы и возмущающих функций
порядка, элементы которых сложным образом зависят от элементов фундаментальной матрицы и возмущающих функций ![]() . В небесной механике для случая
. В небесной механике для случая ![]() и центрального силового поля Ньютона эти сложности преодолеваются некоторыми специальными приёмами [3]. В работе [4] была предложена идея, которая в настоящей статье реализуется для произвольного
и центрального силового поля Ньютона эти сложности преодолеваются некоторыми специальными приёмами [3]. В работе [4] была предложена идея, которая в настоящей статье реализуется для произвольного ![]() и произвольного центрального поля.
и произвольного центрального поля.
Она заключается в том, что:
1. выводится линейное уравнение второго порядка относительно величины ![]() ;
;
2. подстановка выражения для ![]() в уравнения (5) приводит к
в уравнения (5) приводит к ![]() отдельным неоднородным линейным уравнениям для величин
отдельным неоднородным линейным уравнениям для величин ![]() с известными правыми частями:
с известными правыми частями:
 . (6)
. (6)
Перейдем к выводу уравнения для ![]() . Прямым дифференцированием имеем:
. Прямым дифференцированием имеем:
 ,
, 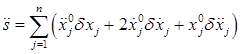 .
.
Используя выражения для ![]() из равенств (5), получаем:
из равенств (5), получаем:
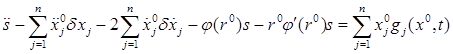 .
.
Подставляя в это равенство ![]() из уравнений (3), получаем:
из уравнений (3), получаем:
 , (7)
, (7)
где использовано обозначение
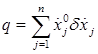 .
.
Далее нам потребуется выражение для производной этой величины. Дифференцируя ее и используя формулы (3) и (5), последовательно выводим:

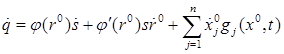 . (8)
. (8)
Дифференцированием равенства (7) получаем:

Используя (8) и простые преобразования приходим к уравнению третьего порядка относительно величины ![]() :
:
 (9)
(9)
Непосредственно видно, что наборы вида  , где
, где ![]() – какой-то па-раметр, от которого зависят координаты
– какой-то па-раметр, от которого зависят координаты ![]() , удовлетворяют однородной системе (5) (т. е. (5), где
, удовлетворяют однородной системе (5) (т. е. (5), где ![]() ). Поэтому из способа вывода следует, что функция вида
). Поэтому из способа вывода следует, что функция вида
 (10)
(10)
удовлетворяет однородному уравнению (9).
Интегрируя (9) в пределах от ![]() до
до ![]() , получаем уравнение второго порядка:
, получаем уравнение второго порядка:

 .
.
Поскольку

то имеем:
 .
.
Итак, получаем:
 (11)
(11)
Если известны три линейно независимые функции ![]() ,
, ![]() ,
,![]() вида (10) , то можно утверждать, что любое решение однородного уравнения (11) имеет вид:
вида (10) , то можно утверждать, что любое решение однородного уравнения (11) имеет вид:
![]()
где: ![]() ,
,![]() ,
,![]() — постоянные.
— постоянные.
Таким образом можно найти фундаментальную систему решений уравнения (11). После этого можно решить и неоднородные уравнения (6).
Для построения модели движения точки в центральных силовых полях часто используют метод малого параметра, то есть рассматривают уравнения вида
![]() ,
, ![]() ,
,
где: ![]() — малый параметр, а решение ищут в виде ряда
— малый параметр, а решение ищут в виде ряда

Оказывается, что функции ![]() удовлетворяют уравнениям в вариациях рассмотренного выше вида, в которых правые части выписываются рекуррентно по
удовлетворяют уравнениям в вариациях рассмотренного выше вида, в которых правые части выписываются рекуррентно по ![]() . В трехмерном случае интерес могут представлять неньютоновые силовые поля (например, поле ядерных сил). В частности, представляет интерес случай, когда
. В трехмерном случае интерес могут представлять неньютоновые силовые поля (например, поле ядерных сил). В частности, представляет интерес случай, когда
![]()
(при![]() это случай силы Ньютона). Тогда:
это случай силы Ньютона). Тогда:
![]() ,
,
а уравнения (3) и (11) принимают вид:
![]() ,
,
![]()
Список литературы:
1.Субботин М.Ф. Введение в теоретическую астрономию // М.: Наука, 1968. — 800 с.
2.Бабаджанянц Л.К., Пупышев Ю.А., Пупышева Ю.Ю. Классическая механика // СПб «СОЛО», 2007. — 240 с.
3.Брауэр Д., Клеменс Дж. Методы небесной механики // М.: Мир, 1964. — 515 с.
4.Бабаджанянц Л.К. Аналитические методы вычисления возмущений в пpямоугольных кооpдинатах планет, 1 // Вестник ЛГУ, —1969. — № 7. — C. 121—132.
дипломов


Оставить комментарий