Статья опубликована в рамках: XXXII Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 26 марта 2014 г.)
Наука: Технические науки
Секция: Строительство и архитектура
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
СФЕРИЧЕСКИЕ И ЦИЛИНДРИЧЕСКИЕ МОРСКИЕ ВОЛНЫ И ИХ ВЛИЯНИЕ НА МОРСКИЕ СООРУЖЕНИЯ
Асланов Лятиф Фирудин оглы
канд. техн. наук, доцент, Азербайджанский архитектурно-строительный университет, Азербайджан, г. Баку
E-mail:
CIVIL ENGINEERING, ARCHITECTURE
Latif Aslanov
candidate of Technical Sciences, Associate Professor of Azerbaijan Architecture and Construction University , Azerbaijani, Baku
АННОТАЦИЯ
Рассмотрены проблемы возникновения сферической и цилиндрической морской волны и влияние их на морские сооружения.
Решены уравнения сферической волны. Определены направляющие косинусы сферы и координаты любой произвольной точки на поверхности сферы. Составлены квадратичные дифференциальные уравнения перемещения u с учетом угла поворота ![]() во времени t при волновом процессе и с помощью формулы Остроградского даны методы решения.
во времени t при волновом процессе и с помощью формулы Остроградского даны методы решения.
Составлены и решены цилиндрические уравнения морской волны. Назначены начальные и граничные условия, удовлетворяющие сферическим и цилиндрическим уравнениям морской волны.
ABSTRACT
The problems of a spherical and cylindrical sea waves and their effect on marine structures.
Solved the equation of a spherical wave. Defined the scope of the direction cosines and the coordinates of any arbitrary point on the surface of the sphere. Composed quadratic differential equations u move with the steering angle θ in time t in a wave process, and using the formula given Ostrogradskii solution methods.
Formulated and solved the equation cylindrical sea wave. Assigned to the initial and boundary conditions that satisfy the equations of spherical and cylindrical sea wave.
Ключевые слова: сферические и цилиндрические волны; радиус сферы и цилиндра; возмущающая сила.
Keywords: spherical and cylindrical waves; the radius of the sphere and cylinder; the disturbing force.
Цель работы. Изучить проблемы возникновения сферической и цилиндрической морской волны и их влияние на свайные фундаменты морских сооружений
Результаты исследований.
Сферические волны. Волны могут иметь сферические и цилиндрические формы при возмущении. Сначала рассмотрим сферические волны. Такую волну можно описать следующим уравнением [4]:
![]() (1)
(1)
Решение этого волнового уравнения будем искать таким образом, чтобы удовлетворяла начальным условиям:
![]() (2)
(2)
Предположим, что ![]() непрерывна со своими производными до третьего порядка, а
непрерывна со своими производными до третьего порядка, а ![]() — до второго порядка включительно относятся к пространственным задачам.
— до второго порядка включительно относятся к пространственным задачам.
По поверхности сферы ![]() радиуса
радиуса ![]() с центром в точке
с центром в точке ![]() решение уравнения (1) выразим интегралом следующего вида:
решение уравнения (1) выразим интегралом следующего вида:
 (3)
(3)
здесь ![]() — произвольная функция. Координаты точек сферы
— произвольная функция. Координаты точек сферы ![]() могут быть выражены по формулам:
могут быть выражены по формулам:
![]() ,
,
где ![]() — направляющие косинусы радиусов сферы
— направляющие косинусы радиусов сферы ![]() . Величины направляющих косинусов радиусов сферы имеют вид:
. Величины направляющих косинусов радиусов сферы имеют вид:
![]()
где угол ![]() меняется от 0 до
меняется от 0 до ![]() и угол
и угол ![]() от 0 до
от 0 до ![]() . Когда точка обладающая координатой (
. Когда точка обладающая координатой (![]() ), описывает сферу
), описывает сферу ![]() , точка (
, точка (![]() ) описывает сферу
) описывает сферу ![]() радиусом, равным единице, с центром в начале координат, а между соответствующими элементами площади
радиусом, равным единице, с центром в начале координат, а между соответствующими элементами площади ![]() обеих сфер имеется соотношение следующего вида:
обеих сфер имеется соотношение следующего вида:
![]() .
.
Тогда интеграл (3) приводится к виду:
 (4)
(4)
Из уравнений (4) видно, что функция ![]() имеет непрерывные производные до к-го порядка, если функция
имеет непрерывные производные до к-го порядка, если функция![]() непрерывна вместе со своими производными до к-го порядка.
непрерывна вместе со своими производными до к-го порядка.
Из формулы (4) находим:

или, возвращаясь к первоначальной области интегрирования получим:
 (5)
(5)
Дифференцируя теперь выражение (4) по ![]() , получаем:
, получаем:
 +
+
 (6)
(6)
Чтобы вычислить ![]() , перепишем (6) в виде:
, перепишем (6) в виде:
 .
.
и, применив формулу Остроградского, получим:
 ,
,
где ![]() — шар радиусом
— шар радиусом ![]() с центром в точке
с центром в точке ![]() .
.
Принимая обозначение

будем иметь
![]() .
.
Дифференцируя это выражение по ![]() , получим
, получим
![]() . (7)
. (7)
Отсюда видно, что
 (8)
(8)
Если переходить в интеграл ![]() сферическим координатам (
сферическим координатам (![]() ) с центром в точке
) с центром в точке ![]() , тогда получим:
, тогда получим:
![]() .
.
Дифференцируя это выражение по ![]() , получим
, получим
 .
.
Сравнивая равенства (5), (7) и (8), мы видим, что функция ![]() , определяемая формулой (3), удовлетворяет волновое уравнение (1), какова бы ни была функция
, определяемая формулой (3), удовлетворяет волновое уравнение (1), какова бы ни была функция ![]() , имеющая непрерывные производные до второго порядка. Из формул (4) и (6) следует, что функция
, имеющая непрерывные производные до второго порядка. Из формул (4) и (6) следует, что функция ![]() удовлетворяет начальным условиям
удовлетворяет начальным условиям
![]() (9)
(9)
Если ![]() удовлетворяет волновое уравнение (1) начальным условиям (9), то легко увидеть, что функция
удовлетворяет волновое уравнение (1) начальным условиям (9), то легко увидеть, что функция
![]() ,
,
будет также решением уравнения (1), удовлетворяющим начальным условиям
![]() (10)
(10)
Теперь, если взять в случае начальных условий (9) за ![]() функцию
функцию ![]() , а в случае начальных условий (10) — функцию
, а в случае начальных условий (10) — функцию ![]() и сложить построенные таким образом решения, получим решение уравнения (1), удовлетворяющее начальным условиям (2).
и сложить построенные таким образом решения, получим решение уравнения (1), удовлетворяющее начальным условиям (2).
Таким образом, решение волнового уравнения (1), удовлетворяющее начальным условиям (2), запишем в виде:
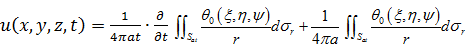 (11)
(11)
Эта формула совпадает с формулой Пуассона по решению сферического волнового уравнения.
Чтобы яснее представить распространения сферических волн в трехмерном пространстве, описываемом формулой (11), необходимо допускать, что начальная возмущающая сила сосредоточена в некоторой ограниченной области ![]() с границей
с границей ![]() , т. е. что функции
, т. е. что функции ![]() равны нулю в области
равны нулю в области ![]() .
.
Допустим точка ![]() находится в области
находится в области ![]() . Обозначим через
. Обозначим через ![]() соответственно наименьшее и наибольшее расстояния от
соответственно наименьшее и наибольшее расстояния от ![]() до точек поверхности
до точек поверхности ![]() (рис. 1).
(рис. 1).
При времени ![]() сфера
сфера ![]() находится вне
находится вне ![]() , обе функции
, обе функции ![]() равны нулю на сфере
равны нулю на сфере ![]() и из формулы (11) имеем
и из формулы (11) имеем ![]() , т.е. начальные возмущения еще не успели дойти до точки
, т.е. начальные возмущения еще не успели дойти до точки ![]() . В момент времени
. В момент времени ![]() сфера
сфера ![]() коснется поверхности
коснется поверхности ![]() и передний фронт волны пройдет через точку
и передний фронт волны пройдет через точку ![]() внутри сферы
внутри сферы ![]() . Начиная с момента времени
. Начиная с момента времени ![]() до момента времени
до момента времени ![]() , сфера
, сфера ![]() будет пересекать область
будет пересекать область ![]() и формула (10) даст
и формула (10) даст ![]() . Наконец, при
. Наконец, при ![]() сфера
сфера ![]() не будет иметь общих точек с поверхностью
не будет иметь общих точек с поверхностью ![]() (вся область
(вся область ![]() будет лежать внутри сферы
будет лежать внутри сферы ![]() ) и из формулы (11) будем иметь
) и из формулы (11) будем иметь ![]() , т. е. начальные возмущения уже прошли через точку
, т. е. начальные возмущения уже прошли через точку ![]() . Моменту времени
. Моменту времени ![]() соответствует прохождение заднего фронта волны через точку
соответствует прохождение заднего фронта волны через точку ![]() . Передний фронт волны в заданный момент времени
. Передний фронт волны в заданный момент времени ![]() представляет собой поверхность, отделяющую точки, которые еще не начали колебаться, от точек, которые уже колеблются. Из этого вытекает, что все точки этой поверхности имеют кратчайшее расстояние от
представляет собой поверхность, отделяющую точки, которые еще не начали колебаться, от точек, которые уже колеблются. Из этого вытекает, что все точки этой поверхности имеют кратчайшее расстояние от ![]() , равное
, равное ![]() . Передний фронт волны есть огибающая для семейства сферической волны, имеющей центр на поверхности
. Передний фронт волны есть огибающая для семейства сферической волны, имеющей центр на поверхности ![]() и радиус
и радиус ![]() . Задний фронт волны в заданный момент времени
. Задний фронт волны в заданный момент времени ![]() представляет собой поверхность, отделяющую точки, которые еще не колеблются, от точек, в которых колебание прекратилось. Постоянная
представляет собой поверхность, отделяющую точки, которые еще не колеблются, от точек, в которых колебание прекратилось. Постоянная ![]() является скоростью распространения фронта волны.
является скоростью распространения фронта волны.

Рисунок 1. Сферическая волна, возникающая от сосредоточенной силы, действующей на ограниченной области ![]() с границей
с границей ![]()
Таким образом, начальные возмущающие силы действуют в локализованном виде в пространстве, вызывая в каждой точке ![]() пространства действие, локализованное во времени; при этом имеет место распространение волны с передним и задним фронтами волны.
пространства действие, локализованное во времени; при этом имеет место распространение волны с передним и задним фронтами волны.
Цилиндрические волны.
От возмущающих сил часто на поверхности жидкости в море возникают цилиндрические волны. В таких волновых явлениях функции ![]() зависят только от
зависят только от ![]() , т.е. сохраняют постоянное значение на всякой прямой, параллельной оси
, т.е. сохраняют постоянное значение на всякой прямой, параллельной оси ![]() . Если передвигать точку
. Если передвигать точку ![]() параллельно оси
параллельно оси ![]() , то правая часть формулы сферической волны (10) не будет менять своего значения, т.е. функция
, то правая часть формулы сферической волны (10) не будет менять своего значения, т.е. функция ![]() также не будет зависеть от
также не будет зависеть от ![]() и формула (10) даст решение уравнения:
и формула (10) даст решение уравнения:
![]() (12)
(12)
при начальных условиях
![]() (13)
(13)
Теперь можем рассматривать решение (11), как исключительно на плоскости ![]() . Для этого надо интегрировать формулу (11), которая относится к сферическим волнам, преобразовать этот интеграл по кругам на плоскости
. Для этого надо интегрировать формулу (11), которая относится к сферическим волнам, преобразовать этот интеграл по кругам на плоскости ![]() . Возьмем точку
. Возьмем точку ![]() на плоскости
на плоскости ![]() . Точки с координатами
. Точки с координатами ![]() , определяемые по формулам:
, определяемые по формулам:
![]() .
.
при ![]() , суть переменных точек сферы
, суть переменных точек сферы ![]() с центром
с центром ![]() и радиусом
и радиусом ![]() . Части этой сферической волны, находящиеся над и под плоскостью
. Части этой сферической волны, находящиеся над и под плоскостью ![]() , проектируются на плоскость
, проектируются на плоскость ![]() в виде круга
в виде круга ![]() с центром
с центром ![]() и радиусом
и радиусом ![]() .
.
Известно, что
![]()
где ![]() – направление нормали к сферической волне
– направление нормали к сферической волне ![]() , т.е. радиуса этой сферы, образующей острый угол с осью
, т.е. радиуса этой сферы, образующей острый угол с осью ![]() . Если принимать переменную точку
. Если принимать переменную точку ![]() на поверхности сферы,
на поверхности сферы, ![]() – ее проекция на плоскость
– ее проекция на плоскость ![]() , то
, то
![]() ,
,
где: (![]() ) — координаты переменной точки круга
) — координаты переменной точки круга ![]() .
.
В результате преобразования формулы сферической волны (11) , получим:
 (14)
(14)
Формула (14) даст решение цилиндрического волнового уравнения (12) удовлетворяющее начальным условиям (13).
Объяснением возникновения цилиндрической волны будет следующее. Допустим, что начальная возмущающая сила ограничивается некоторой граничной областью ![]() на плоскости
на плоскости ![]() с контуром
с контуром ![]() , т. е.
, т. е. ![]() и
и ![]() равны нулю вне
равны нулю вне ![]() . Пусть точка
. Пусть точка ![]() лежит вне области
лежит вне области ![]() . Для моментов времени
. Для моментов времени ![]() , где
, где ![]() — наименьшее расстояние от
— наименьшее расстояние от ![]() до контура
до контура ![]() , круг
, круг ![]() не имеет общих точек с областью
не имеет общих точек с областью![]() , функции
, функции ![]() и
и ![]() равны нулю во всем круге
равны нулю во всем круге ![]() и формула (14) дает
и формула (14) дает ![]() — до точки
— до точки ![]() возмущение еще не дошло. В момент времени
возмущение еще не дошло. В момент времени ![]() в точку
в точку ![]() придет передний фронт волны. Для значений
придет передний фронт волны. Для значений ![]() , где
, где ![]() — наибольшее расстояние от
— наибольшее расстояние от ![]() до контура
до контура ![]() , круг
, круг ![]() будет содержать внутри себя всю область
будет содержать внутри себя всю область ![]() и мы получим.
и мы получим.
 (15)
(15)
После момента времени ![]() функция
функция ![]() не обращается в нуль, как в случае трехмерного сферического пространства волны. Но ввиду присутствия члена
не обращается в нуль, как в случае трехмерного сферического пространства волны. Но ввиду присутствия члена ![]() в знаменателе можно утверждать, что
в знаменателе можно утверждать, что ![]() при
при ![]() . Таким образом, начальная возмущающая сила, локализованная на плоскости, не локализовано во времени создает цилиндрическую волну, которая имеет передний фронт волны, но не имеет заднего фронта. В трехмерном пространстве уравнению (13) соответствуют цилиндрические волны.
. Таким образом, начальная возмущающая сила, локализованная на плоскости, не локализовано во времени создает цилиндрическую волну, которая имеет передний фронт волны, но не имеет заднего фронта. В трехмерном пространстве уравнению (13) соответствуют цилиндрические волны.
На основании вышеизложенного можно сделать следующие выводы:
1. При возмущении моря от ветровой и другой силы могут возникать сферические и цилиндрические волны, которые влияют на устойчивость и несущую способность свайных фундаментов, как оснований морских сооружений. Большой интерес представляют составить и решить волновые уравнения этих явлений.
2. Предложены методы составления и решения дифференциальных уравнений сферической и цилиндрической волны с помощью тригонометрических функций и функций перемещения точки, принятые на поверхности сферы и цилиндра с произвольным радиусом r и углом поворота ![]() . Назначены начальные и граничные условия, удовлетворяющие уравнения сферической и цилиндрической волны.
. Назначены начальные и граничные условия, удовлетворяющие уравнения сферической и цилиндрической волны.
Список литературы:
1.Асланов Л.Ф. Комбиниран реологически модел за описване на линейно еластично напрегнато състояние на шельфа (на болгарском яз.). Сб. с доклади ІІ. Шеста Международна научна конференция «Архитектура, Строительство-съвременност», 30 май — 1 юни 2013 г. гр. Варна, България, — с. 159—166.
2.Асланов Л.Ф. Структура турбулентного потока волны и влияние ее на конструкции свайного фундамента морских сооружений. Вісник НТУУ «КПІ», серія «Гірництво», вип.. 23 К.: 2014. — с. 5—12.
3.Асланов Л.Ф. Расчет понтона и всплытия опорного блока при различных глубинах моря для освоения нефтегазовых месторождений. Международнaя научно-практическая конференция. Геленджик, Краснодарский край, 2010 г., — ст. 67—72
4.Кошляков Н.С., Глинер Э.Б., Смирнов М.М. Уравнения в частных производных математической физики. Изд. «Высшая школа», М.: 1970. — 710 с.
дипломов


Оставить комментарий