Статья опубликована в рамках: XXXIX Международной научно-практической конференции «Технические науки - от теории к практике» (Россия, г. Новосибирск, 22 октября 2014 г.)
Наука: Технические науки
Секция: Информатика, вычислительная техника и управление
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
Статья опубликована в рамках:
Выходные данные сборника:
ЧИСЛЕННОЕ МОДЕЛИРОВАНИЕ ДИСПЕТЧЕРОВ ЗАДАЧ СО СТРАТЕГИЕЙ РАЗДЕЛЕНИЯ В ПРОСТРАНСТВЕ ДЛЯ МНОГОПРОЦЕССОРНЫХ СИСТЕМ НА ОСНОВЕ СЕТЕЙ МАССОВОГО ОБСЛУЖИВАНИЯ
Мартышкин Алексей Иванович
канд. техн. наук, доцент кафедры Вычислительных машин и систем Пензенского государственного технологического университета, РФ, г. Пенза
NUMERICAL SIMULATION OF TASK MANAGER WITH THE STRATEGY OF SEPARATED IN SPACE FOR MULTIPROCESSOR SYSTEMS BASED ON QUEUEING NETWORKS
Alexey Martyshkin
candidate of Science, assistant professor Department of Computational Systems and Machines of Penza State Technological University, Russia, Penza
Работа выполнена при финансовой поддержке стипендии Президента РФ молодым ученым т аспирантам на 2012—2014 гг. (СП-1172.2012.5).
АННОТАЦИЯ
Целью статьи является проведение моделирования для анализа производительности диспетчера задач со стратегией разделения в пространстве в многопроцессорной системе. Методы исследования основаны на положениях теории систем и сетей массового обслуживания и теории вероятностей. В статье приводится численное моделирование диспетчеров задач для многопроцессорных систем на основе разомкнутых сетей массового обслуживания. Результатами работы являются выражения для расчета характеристик представленной системы: для каждого класса задач в отдельности и для суммарного потока задач. Сделаны выводы.
ABSTRACT
The purpose of the article is to conduct modeling for analyze the performance of Task Manager with the strategy of separation in space in a multiprocessor system. Research methods based on the provisions theory of systems and networks, queuing theory and probability theory. The article provides a numerical simulation of Task Managers for multiprocessor systems based on open queuing networks. Result is the expression for calculating the characteristics of the present system: for each class of tasks separately and for a total stream problems. The conclusions made.
Ключевые слова: математическая модель; диспетчер задач; разделение в пространстве; случайный процесс; система массового обслуживания; приоритет; вероятность.
Keywords: mathematical model; task manager; space division; the stochastic process; queuing system; priority; probability.
Изучая сложные системы со случайным характером функционирования, полезной математической моделью является стохастический процесс, который развивается в зависимости от ряда случайных факторов.
Примером случайных процессов могут служить процессы, связанные с диспетчеризацией задач в многопроцессорных системах. Большая часть моделей систем со стохастическим характером функционирования строится на основе моделей массового обслуживания, процессы в которых являются случайными и, зачастую, марковскими, либо каким-то образом связанные с марковскими процессами, применение которых оказывается особенно эффективным и результативным при исследовании систем и сетей массового обслуживания с накопителями ограниченной емкости.
Математическая модель диспетчера задач (ДЗ) со стратегией разделения в пространстве [2, 4] состоит из n-одноканальных СМО (S1,…,Sm) (см. рис. 1). Каждая такая СМО моделирует обслуживание в ДЗ и центральном процессоре (ЦП) (S1, S2,…, Sm). Источник S0 моделирует потоки заявок ![]() и поглощает обслуженные заявки. Перед ДЗ формируются очереди с ограничением числа мест. В систему поступает неоднородный поток задач. Ожидающие обслуживания задачи разнесены по очередям ограниченной емкости. Между задачами разных классов установлены относительные приоритеты (ОП), означающие, что всякий раз из очередей на обслуживание выбирается задача с самым высоким приоритетом. При этом при поступлении в систему высокоприоритетной задачи обслуживание низкоприоритетной не прерывается. При заполненных очередях поступившая задача теряется. ДЗ и ЦП представляются в виде одноканальной СМО.
и поглощает обслуженные заявки. Перед ДЗ формируются очереди с ограничением числа мест. В систему поступает неоднородный поток задач. Ожидающие обслуживания задачи разнесены по очередям ограниченной емкости. Между задачами разных классов установлены относительные приоритеты (ОП), означающие, что всякий раз из очередей на обслуживание выбирается задача с самым высоким приоритетом. При этом при поступлении в систему высокоприоритетной задачи обслуживание низкоприоритетной не прерывается. При заполненных очередях поступившая задача теряется. ДЗ и ЦП представляются в виде одноканальной СМО.
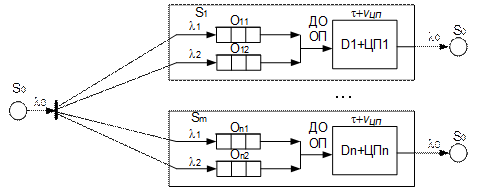
Рисунок 1. Схема математической модели n-процессорной системы с индивидуальными диспетчерами
Рассматриваемая система является одноканальной. Входящий поток задач — неоднородный: в систему поступает два потока пользовательских задач разного приоритета. Очереди для задач каждого класса являются ограниченными по длине. Для примера, в данной работе длина очередей принята одинаковой и равной ![]()
Дисциплина буферизации – без вытеснения задач: если при поступлении в систему задачи любого класса соответствующая очередь заполнена до конца, то задача теряется. Дисциплина обслуживания – с относительными приоритетами: задачи первого класса имеют высший приоритет по отношению к задачам второго класса [1, 5].
Поступающие в систему задачи двух классов образуют простейшие потоки с интенсивностями ![]() и
и ![]() соответственно.
соответственно.
Длительности обслуживания задач каждого класса распределены по экспоненциальному закону с интенсивностями ![]() и
и ![]() , где
, где ![]() и
и ![]() соответственно средние длительности обслуживания задач класса 1 и 2.
соответственно средние длительности обслуживания задач класса 1 и 2.
Для описания состояний марковского процесса будем использовать распределение задач между ДЗ и очередями. Закодируем состояния следующим образом: Хi: (Д/О1, О2), где Д= {0, 1, 2} — состояние ДЗ, задаваемое классом задачи, находящейся на обслуживании («0» — ДЗ; «1» или «2» — на обслуживании находится задача класса 1 или 2); О1, О2= {0,1} — состояние очередей 1 и 2 («0» — отсутствие задачи в очереди, «1» — наличие одной задачи в очереди соответствующего класса). При таком предложенном способе кодирования система может находиться в следующих состояниях (рис. 2):
X 0: (0/0,0) — в системе нет ни одной задачи;
X 1: (1/0,0) — на обслуживании находится задача класса 1;
X 2: (2/0,0) — на обслуживании находится задача класса 2;
X 3: (1/1,0) — на обслуживании находится задача класса 1 и одна задача класса 1 ожидает обслуживания в очереди О11;
X 4: (1/0,1) — на обслуживании находится задача класса 1 и одна задача класса 2 ожидает обслуживания в очереди О12;
X 5: (2/1,0) — на обслуживании находится задача класса 2 и одна задача класса 1 ожидает обслуживания в очереди О11;
X 6: (2/0,1) — на обслуживании находится задача класса 2 и одна задача класса 2 ожидает обслуживания в очереди О12;
X 7: (1/1,1) — на обслуживании находится задача класса 1 и по одной задачи класса 1 и 2 ожидают обслуживания в очередях О11 и О12;
X 8: (2/1,1) — на обслуживании находится задача класса 2 и по одной задачи класса 1 и 2 ожидают обслуживания в очередях О11 и О12;

Рисунок 2. Размеченный граф переходов
В каждый момент времени происходит только одно событие: либо поступление задачи какого-либо класса, либо завершение обслуживания задачи в ДЗ, поскольку вероятность появления двух и более событий в один и тот же момент времени равна нулю [1, 3].
При наличии в очередях задач первого и второго приоритетов (состояния Х7 и Х8) после завершения обслуживания некоторой задачи в ДЗ случайный процесс переходит в состояние Х4, означающее, что на обслуживание всегда выбирается высокоприоритетная задача класса 1.
По графу переходов составим систему уравнений для определения стационарных вероятностей:
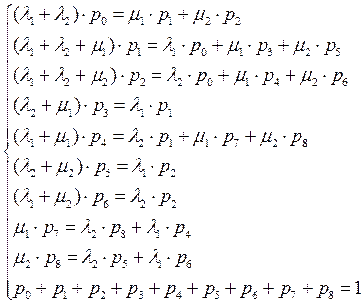 (1)
(1)
Расчет характеристик представленной системы будем производить двумя способами: 1) для каждого класса задач; 2) для суммарного потока задач.
Расчет характеристик обслуживания задач каждого класса (приоритета) выполняется по следующим выражениям:
а. нагрузка на ДЗ

 (2)
(2)
б. загрузка, создаваемая потоком задач, которая может характеризоваться вероятностью того, что на обслуживании в ДЗ находится задача класса 1 или 2 соответственно
![]()
![]() (3)
(3)
в. среднее число задач в очередях перед ДЗ
![]()
![]() (4)
(4)
г. среднее число задач в очередях и на обслуживании
![]()
![]() (5)
(5)
д. вероятность потери задач из-за переполнения очередей
![]()
![]() (6)
(6)
е. производительность по каждому классу (приоритету) задач
![]()
![]() (7)
(7)
ж. среднее время ожидания задач в очередях

 (8)
(8)
з. среднее время пребывания задач в системе
![]()
![]() (9)
(9)
Расчет характеристик обслуживания задач суммарного потока выполняется по следующим выражениям:
1) суммарная нагрузка на ДЗ
![]() (10)
(10)
2) суммарная загрузка системы
![]() (11)
(11)
3) коэффициент простоя системы
![]() (12)
(12)
4) суммарное число задач в очередях
![]() (13)
(13)
5) суммарное число задач в системе
![]() (14)
(14)
6) вероятность потери задач
![]() (15)
(15)
7) производительность системы
![]() (16)
(16)
8) среднее время ожидания в очередях задач суммарного потока
![]() (17)
(17)
9) среднее время пребывания задач суммарного потока
![]() (18)
(18)
Ниже приведены полученные графики численного моделирования ДЗ со стратегией разделения в пространстве (рис. 3, рис. 4).

Рисунок 3. Зависимость латентности диспетчера задач от интенсивности неоднородного входного потока задач

Рисунок 4. Зависимость времени ответа системы от интенсивности неоднородного входного потока задач
Были получены выражения для численного расчета основных вероятностно-временных характеристик ДЗ со стратегией разделения в пространстве. Расчет характеристик представленной системы производился двумя способами: а) для каждого класса задач; б) для суммарного потока задач.
Список литературы:
1.Алиев Т.И. Основы моделирования дискретных систем. СПб.: СПбГУ ИТМО, 2009. — 363 с.
2.Бикташев Р.А., Мартышкин А.И. Моделирование диспетчеров задач многопроцессорных систем // Успехи современного естествознания: Научно-теоретический журнал. — 2012. — № 6. — С. 83—85.
3.Вентцель Е.С. Введение в исследование операций. М.: "ЁЁ Медиа", 2012. — 390 с.
4.Мартышкин А.И. Исследование диспетчеров задач многопроцессорных систем на моделях массового обслуживания // XXI век: итоги прошлого и проблемы настоящего плюс: Научно-методический журнал. Пенза: Пенз. гос. технол. академия. — 2012. — № 5. — С. 139—146.
5.Таненбаум Э. Современные операционные системы. 3-е изд. СПб.: Питер, 2010. — 1120 с.
дипломов


Оставить комментарий