ПРИМЕНЕНИЕ  МЕТОДА  МОНТЕ-КАРЛО  ДЛЯ  ОЦЕНКИ  ИНВЕСТИЦИОННЫХ  ПРОЕКТОВ

Ефремова  Елена  Алексеевна

студент  5  курса,  кафедры  ММиМЭ,  ОГУ,  РФ,  г.  Оренбург

E-mail: 

Прядкина  Вера  Алексеевна

студент  5  курса,  кафедры  ММиМЭ,  ОГУ,  РФ,  г.  Оренбург

E-mail: 

Инвестиции  представляют  собой  долгосрочные  вложения  финансовых  и  экономических  ресурсов  с  целью  получения  доходов  в  будущем.  Они  являются  ключевым  фактором  при  создании  или  развитии  организации,  реализации  инвестиционного  проекта.  При  этом  важно  весь  инвестиционный  процесс  в  целом:  предварительный  анализ,  мониторинг,  коррекция  инвестиционного  проекта  в  процессе  выполнения  и  его  завершение.

Наиболее  важным  элементом  анализа  инвестиционных  проектов  является  оценка  рисков.  Риск  —  это  возможность  возникновения  в  ходе  реализации  проекта  условий,  при  которых  наступят  негативные  последствия  для  участников  проекта  и  значительное  сокращение  или  отсутствие  доходов  инвестиционного  проекта  [6].

Инвестиционный  риск  —  это  такой  риск,  в  результате  которого  происходит  обесценивание  вложений  капитала,  возникает  опасность  потери  инвестиций  (или  неполучения  полной  отдачи  от  них)  и  непредвиденных  финансовых  потерь  (утрата  доходов,  капитала,  снижение  прибыли)  в  ситуации  неопределенности  условий  инвестирования  средств  [3].

Показатели  и  методы  оценки  эффективности  инвестиционного  проекта  используются,  во-первых,  для  определения  эффективности  инвестиционного  проекта  (когда  необходимо  принять  решение:  утвердить  или  отклонить  проект);  во-вторых,  для  сравнения  альтернативных  инвестиционных  проектов  (если  требуется  выбрать  проект  из  нескольких  альтернативных).

Методы  количественной  оценки  предполагают  численное  определение  величины  риска  инвестиционного  проекта.  Если  точные  оценки  параметров  задать  невозможно,  однако  есть  возможность  определить  интервалы  возможного  колебания  показателей.  В  этом  случае  можно  использовать  метод  имитационного  моделирования  Монте-Карло,  который  формирует  множество  возможных  случайных  сценариев.  Результат  анализа  риска  выражается  в  виде  вероятности  [1].

Практическое  применение  данного  метода  продемонстрировало  широкие  возможности  его  использования  в  инвестиционном  проектировании,  особенно  в  условиях  неопределённости  и  риска. 

Идея  метода  заключается  в  соединении  анализа  чувствительности  и  вероятностных  распределений  факторов  модели.  Вместо  создания  отдельных  сценариев  (наилучший,  наихудший  и  наиболее  вероятный),  в  имитационном  методе  генерируются  сотни  возможных  комбинаций  факторов  с  учётом  их  вероятностного  распределения.  [6]

Алгоритм  метода  Монте-Карло  включает  следующие  этапы:

1.  установление  взаимосвязи  между  исходными  и  выходными  показателями  в  виде  математического  уравнения  или  неравенства;

2.  задание  законов  распределения  вероятностей  для  ключевых  параметров  модели;

3.  проведение  компьютерной  имитации  значений  ключевых  параметров  модели. 

4.  расчет  основных  характеристик  распределений  исходных  и  выходных  показателей; 

5.  проведение  анализа  полученных  результатов  (графический  и  количественный)  и  принятие  решения. 

Рассмотрим  применение  метода  Монте-Карло  на  примере  инвестиционного  проекта  для  строительной  компании,  которая  рассматривает  вопрос  о  приобретении  патента  для  последующего  производства  нового  вида  строительного  материала.  Данный  материал  отличается  высокой  прочностью,  низкой  теплопроводностью,  водонепроницаемостью  и  хорошей  звукоизоляцией.  Стоимость  патента  составляет  $  3,4  млн.  Срок  проекта  составляет  три  года.  Рынок  строительных  материалов  является  весьма  конкурентным.  Конкуренция  со  стороны  других  материалов  может  привести  к  снижению  цены  ниже  предполагаемой.  Также  из-за  влияния  конкуренции  трудно  точно  предсказать  объем  продаж  строительного  материала.  Помимо  цены  и  объема  продаж  не  поддаются  точному  прогнозу  будущая  себестоимость  материала  и  операционные  издержки.  Очень  часто  себестоимость  и  издержки  превышают  прогнозируемые.  Кроме  того,  они  могут  колебаться  год  от  года.  Основная  информация  по  проекту  представлена  в  таблице  1.  Себестоимость  и  операционные  издержки  рассчитываются  как  некоторый  процент  от  объема  продаж.

Таблица  1. 

Характеристики  инвестиционного  проекта

Составим  математическую  модель  задачи. 

Рассмотрим  движение  денежных  средств  как  численный  ряд,  состоящий  из  последовательности  распределенных  во  времени  денежных  платежей  CF₀,  CF₁,…,CF_n.  Каждый  элемент  этого  ряда  CF_t  представляет  собой  разность  между  всеми  поступлениями  денежных  средств  и  расходами  на  заданном  временном  отрезке  проведения  финансовой  операции.  Таким  образом,  величина  CF_t  может  иметь  как  положительный,  так  и  отрицательный  знак.

Математическая  модель  согласно  исходной  постановке  задачи  имеет  следующий  вид:

,  (1)

где:  Т  —  ставка  налога  на  прибыль;

r  —  ставка  дисконтирования;

P  —  цена  упаковки;

Q  —  объем  продаж;

C  —  себестоимость;

V  —  операционные  издержки.

Рассмотрим  основные  показатели  оценки  эффективности  инвестиционных  проектов:

1.  чистый  приведенный  доход  (стоимость)  —  разность  между  дисконтированными  показателями  чистого  дохода  и  первоначальными  инвестициями  [4];

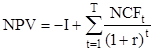,  (2)

где:  NCF_t  —  чистый  денежный  доход  для  t-го  периода;

T  —  число  плановых  периодов;

r  —  ставка  дисконтирования;

I  —  первоначальные  инвестиции.

Если  чистый  приведенный  доход  имеет  положительный  знак  (NPV>0),  это  означает,  что  в  течение  своей  экономической  жизни  проект  возместит  первоначальные  затраты  I,  обеспечит  получение  прибыли  согласно  заданной  ставке  дисконтирования  r,  а  также  ее  некоторый  резерв,  равный  NPV.  Если  чистый  приведенный  доход  имеет  отрицательный  знак  (NPV<0),  то  проект  убыточен.  Если  чистый  приведенный  доход  равен  нулю  (NPV=0),  то  проект  только  окупает  первоначальные  затраты  и  не  приносит  дохода.

2.  внутренняя  норма  доходности  (IRR)  —  такая  расчетная  ставка,  при  которой  первоначальные  инвестиционные  затраты  окупаются,  но  не  приносят  прибыль  [4];

Если  r<IRR,  то  инвестиции  имеют  смысл,  в  противном  случае  проект  отклоняется.

3.  дисконтированный  индекс  рентабельности  (DPI)  характеризует  доход,  приходящийся  на  единицу  затрат;

Чтобы  проект  был  приемлемым  дисконтированный  индекс  рентабельности  должен  быть  больше  единицы  (DPI>1). 

Если  величина  критерия  DPI>1,  то  современная  стоимость  денежного  потока  проекта  превышает  первоначальные  инвестиции,  тем  самым  обеспечивая  наличие  положительной  величины  NPV.  В  этом  случае  проект  следует  принять.  При  DPI=1  величина  NPV=0,  и  инвестиции  не  приносят  дохода.  Если  DPI<1,  то  проект  не  обеспечивает  заданного  уровня  рентабельности  и  его  следует  отклонить  [4].

4.  дисконтный  срок  окупаемости  (DPP)  —  число  лет,  необходимое  для  того,  чтобы  сумма  дисконтированных  на  момент  окончания  инвестиционных  затрат  чистых  доходов  была  равна  размеру  инвестиций  [4];

Для  реализации  метода  Монте-Карло  для  данного  примера  разработано  специальное  программное  средство  в  среде  программирования  Delphi  7.0  для  проведения  имитационных  расчетов  прибыльности  инвестиционного  проекта,  которое  необходимо  по  следующим  причинам:  осуществление  многократного  повторения  имитационных  экспериментов,  значительное  упрощение  обработки  результатов  имитаций,  графическое  представление  результатов.

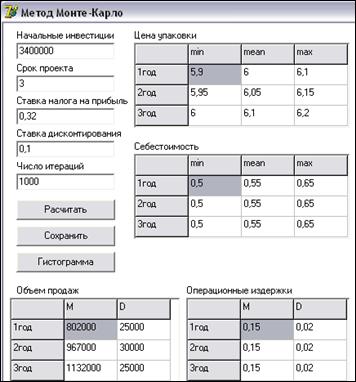
Рисунок  1.  Ввод  исходных  данных

Рисунок  2.  Результаты  работы  программного  средства  «Метод  Монте-Карло»

Согласно  рисунку  2,  среднее  значение  чистого  приведенного  дохода  (NPV)  составило  218352,445  $.  Отсюда  следует,  что  в  течение  своей  экономической  жизни  проект  возместит  первоначальные  затраты,  обеспечит  получение  прибыли. 

Внутренняя  норма  доходности  (IRR)  составила  в  среднем  13,4  %.  Так  как  r<IRR,  т.  е.  10  %<13,4  %,  инвестиции  имеют  смысл,  проект  следует  принять.

Дисконтированный  индекс  рентабельности  (DPI)  составил  1,064,  т.  е.  современная  стоимость  денежного  потока  проекта  превышает  первоначальные  инвестиции,  обеспечивая  тем  самым  наличие  положительной  величины  NPV.  При  этом  норма  рентабельности  превышает  единицу,  и  проект  следует  принять.

Дисконтный  срок  окупаемости  (DPP)  составил  2,825,  т.  е.  сумма  дисконтированных  на  момент  окончания  инвестиций  чистых  доходов  станет  равной  размеру  инвестиций  через  2  года  и  10  месяцев.  А  так  как  срок  данного  проекта  3  года,  то  можно  заключить,  что  проект  возместит  первоначальные  вложения  в  заданный  срок.

Анализ  по  методу  Монте-Карло  показывает:  вероятность  того,  что  NPV  проекта  будет  положительный,  не  является  стопроцентной.  Согласно  гистограмме  распределения  NPV,  существует  вероятность  (почти  10  %)  того,  что  NPV  проекта  окажется  отрицательным.  Таким  образом,  в  10  %  всех  случаев  при  определенной  комбинации  факторов  компания  понесет  потери.  В  то  же  время  при  благоприятном  стечении  факторов  NPV  проекта  может  превышать  693467,445  $.

Таким  образом,  с  помощью  метода  Монте-Карло  была  проведена  оценка  рисков  инвестиционного  проекта  для  строительной  компании  при  различных  комбинациях  факторов.  В  целом  проект  оказался  прибыльным  и  руководству  компании  рекомендуется  приобрести  патент  для  последующего  производства  нового  вида  строительного  материала.

Список  литературы:

1.Гранатуров  В.М.  Экономический  риск:  сущность,  методы  измерения,  пути  снижения  [Текст]  :  учеб.  пособие  для  вузов  /  В.М.  Гранатуров.  2-е  изд.,  перераб.  и  доп.  М.  :  Дело  и  Сервис,  2002.  —  160  с. 

2.Дубров  А.М.  Моделирование  рисковых  ситуаций  в  экономике  и  бизнесе  :  учеб.  пособие  для  вузов  /  А.М.  Дубров  [и  др.];  под  ред.  Б.А.  Лагоши.  2-е  изд.,  перераб.  и  доп.  М.:  Финансы  и  статистика,  2001.  —  224  с. 

3.Королев  В.Ю.  Математические  основы  теории  риска  /  Королев  В.Ю.,  Бенинг  В.Е.,  Шоргин  С.Я.:  Учебн.  пособ.  М.:  ФИЗМАТЛИТ,  2007.  —  544  с.

4.Челмакина,  Л.  Оценка  эффективности  инвестиционных  проектов  /  Л.  Челмакина  //  Проблемы  теории  и  практики  управления,  —  2007.  —  №9.  —  с.  69—75.

5.Чернов  И.В.  Разработка  и  защита  инвестиционных  бизнес-проектов  /  Чернов  И.В.  //  Финансовый  менеджмент,  —  2007.  —  №  5.  —  с.  39—54.

6.Шапкин  А.С.  Теория  риска  и  моделирование  рисковых  ситуаций  /  Шапкин  А.С.,  Шапкин  В.А.:  Учебник.  М.:  Издательско-торговая  корпорация  «Дашков  и  К˚»,  2006.  —  880  с.