МОДЕЛИРОВАНИЕ  МОНОПОЛИСТИЧЕСКОЙ  КОНКУРЕНЦИИ  В  УСЛОВИЯХ  НЕОПРЕДЕЛЕННОСТИ  ПРИ  CES   ПРЕДПОЧТЕНИЯХ  ПОТРЕБИТЕЛЕЙ

Чернова  Надежда  Дмитриевна

студент  2  курса  магистратуры,  кафедра  прикладной  математики,  Финансовый  университет  при  Правительстве  РФ,  РФ,  г.  Москва

E -mail:  nadezda.ch.91@gmail.com

Шаповал  Александр  Борисович

научный  руководитель,  д-р  физ.-мат.  наук,  профессор,  кафедра  прикладной  математики,  Финансовый  университет  при  Правительстве  РФ,  РФ,  г.  Москва

На  протяжении  достаточно  долгого  периода  времени  центральное  место  в  теории  международной  торговли  принадлежало  моделям  международной  конкуренции  и  специализации  [1,  c.  45].  Эти  модели  применимы  в  тех  случаях,  когда  встречные  потоки  товаров  между  двумя  торгующими  странами  существенно  различаются  по  своему  составу,  то  есть  представляют  собой  продукцию  разных  отраслей.  Такой  тип  торговли  можно  назвать  межотраслевым.  Основной  задачей  таких  моделей  было  объяснить  выгоду,  направление  торговли  и  ее  международную  специализацию. 

Однако  в  60—70-х  гг.  XX  столетия  начали  проявляться  черты  внутриотраслевой  торговли  [1,  c.  45].  Страны  стали  обмениваться  товарами,  представляющими  одну  отрасль:  например,  автомобилями,  бытовой  техникой,  продуктами  питания  и  проч.  Также  характерной  чертой  современной  торговли  является  наличие  множества  разновидностей,  брендов  одних  и  тех  же  товаров,  выпускаемых  множеством  фирм.  Этому  способствуют  гигантские  супер-  и  гипермаркеты,  вмещающие  огромное  количество  товаров.  Основными  сетями  этих  магазинов  владеют  мультинациональные  компании  (МНК),  что  способствует  тому,  что  часто  в  разных  странах  предлагаются  для  продажи  одни  и  те  же  наборы  брендов,  и  огромные  потоки  схожих  товаров  перемещаются  между  странами  [1,  c.  45].

Внутриотраслевая  торговля,  в  отличие  от  межотраслевой,  основана  на  сходстве  торгующих  стран  (сходство  уровней  развития,  предпочтений  потребителей,  технологий).  В  связи  с  этим  в  конце  1970-х  гг.  Авинашем  Дикситом  и  Джозефом  Стиглицем  была  разработана  модель  монополистической  конкуренции,  в  основу  которой  легла  теория  монополистической  конкуренции  Чемберлина.  В  настоящее  время  теория  Диксита-Стиглица  является  составной  частью  макроэкономики  и  смежных  научных  областей  [3,  c.  2].

На  основе  модели  Диксита-Стиглица  была  разработана  теория  о  предпочтениях  потребителей  при  постоянной  взаимозаменяемости  товаров.  Проблема  CES-предпочтений  изучалась  многими  специалистами  (Комбс,  Майер,  Тисс,  2008;  Жеболодько,  Коковин,  Тисс,  2010).  Однако  эта  теория  была  развита  дальше  и  была  введена  модель  с  неопределенными  макроэкономическими  переменными  (Шаповал,  Гончаренко,  2013).

Рассмотрим  основные  положения  теории  Диксита-Стиглица.  Согласно  ей,  экономика  состоит  из  двух  секторов:  сельскохозяйственного  и  промышленного.  В  сельскохозяйственном  секторе  однородные  товары  производятся  при  постоянной  прибыли  и  продаются  на  совершенноконкурентном  рынке.  В  промышленном  же  секторе  фирмы  производят  дифференцированные  товары  при  увеличивающихся  доходах  и  продают  его  на  рынке  монополистической  конкуренции. 

В  экономике  существует  L  потребителей  с  одинаковыми  предпочтениями.  Эти  предпочтения  соответствуют  функции  полезности  Кобба-Дугласа:

  ,  0  <  μ  <  1  (1)

где:  А  —  количество  сельскохозяйственного  товара;

С  —  это  константа,  выбранная  таким  образом,  что  коэффициент  косвенной  полезности  нормирован  к  1;

М   —  количество  совокупного  дифференцированного  товара  промышленного  производства  и  может  быть  выражена  через  CES-индекс 

  ,    [2,  с.  55].  (2) 

В  формуле  (2)  используются  следующие  обозначения: 

q_i   —  количество  потребляемого  товара  вида  i;

n   —  общее  количество  имеющихся  видов  товара;

ρ   —  параметр,  обозначающий  величину,  обратную  к  степени  дифференциации  видов  товара. 

Определим,  какую  часть  своих  средств  они  тратят  на  промтовары  и  сельскохозяйственные  товары.  Для  этого  необходимо  решить  систему  вида:

    ,    (3)

Для  определения  количества  потребляемого  товара,  то  есть  спроса  на  него,  при  заданной  величине  расходов  Е  потребителя  следует  решать  задачу 

          (4)

Решением  данной  задачи  будет  являться 

,                  (5)

Выражение  (5)  представляет  собой  функцию  совокупного  спроса  на  товар  вида  i.  Данное  уравнение  показывает,  что  если  одна  из  фирм  установит  цену  выше,  чем  у  конкурентов,  то  это  приведет  к  уменьшению  потребления  соответствующего  товара,  но  так  как  потребители  предпочитают  потреблять  различные  товары,  то  спрос  на  данный  вид  товара  останется  положительным.  Также  это  выражение  обозначает,  что  добавление  нового  вида  товара  увеличивает  знаменатель,  что  в  свою  очередь  ведет  к  снижению  потребления  уже  имеющихся  видов  товара  до  тех  пор,  пока  цены  остаются  неизменными.

Помимо  потребителей  в  модели  рассматриваются  также  и  фирмы.  В  сельскохозяйственном  секторе  используется  только  неквалифицированная  рабочая  сила.  Предположим,  что  существует  совершенная  конкуренция  и  постоянная  прибыль,  таким  образом,  цена  сельскохозяйственного  товара  p_a  равна  предельным  издержкам,  которые  в  свою  очередь  равны  произведению  предельной  рабочей  силы  и  заработной  платы  в  сельскохозяйственном  секторе:  .  Предположим,  что  один  работник  производит  один  товар,  поэтому  m_a  =  1.  Следовательно,  цена  этого  товара  равна  заработной  плате  неквалифицированных  рабочих.  Поскольку  сельскохозяйственные  товары  являются  единицей  исчисления,  то  p_a  =  w_a  =  1. 

Каждая  фирма  продает  только  один  вид  товара,  при  этом  не  существует  двух  фирм,  продающих  одинаковые  товары,  что  привело  бы  к  ценовой  конкуренции.  Следовательно,  n  видов  промышленных  товаров  продаются  n  различными  фирмами.  Таким  образом,  можно  определить  количество  видов  товара  как  количество  фирм.  Технологии  производства  одинаковы  везде  и  для  всех  товаров,  здесь  нет  сравнительных  преимуществ. 

Задача  фирмы  состоит  в  максимизации  своей  прибыли

  ,  (6)

где  спрос  q_i  задан  функцией    [2,  с.  63].

Решив  задачу  фирмы  можно  найти  оптимальное  количество  товара  q*,  выпускаемое  каждой  фирмой,  а  также  равновесную  цену  на  товары  фирм  p*:

  ,  (7)

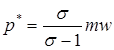  .  (8)

Поскольку  фирма  использует  квалифицированную  рабочую  силу  в  количестве  ,  то  количество  фирм  n*  можно  определить  из  условия  полной  занятости:

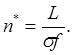    (9)

n*  не  обязательно  может  являться  целым  числом.  Поэтому  значение  n*  берется  как  наибольшее  целое  число  меньше  и  равное  n*.  Увеличение  экономики  не  отражается  на  размере  фирм,  но  на  уровне  рынка  есть  скалярный  эффект:  чем  больше  увеличение  количества  работников  (потребителей)  L,  тем  сильнее  увеличение  количества  фирм  и,  следовательно,  количества  видов  товара.  До  тех  пор,  пока  постоянные  издержки  превосходят  0,  количество  фирм  и  разновидностей  товара  конечно.

Равновесная  зарплата  работников  выражается  как 

  .  (10)

Итак,  можно  сделать  вывод,  что  равновесие  на  рынке  монополистической  конкуренции  задается  четырьмя  выражениями  параметрами:  q*,  p*,  n*,  w*.

Как  уже  известно,  размеры  фирм  в  отрасли  достаточно  малы  по  отношению  к  рынку  в  целом,  поэтому  каждая  из  них  считает,  что  ее  решение  относительно  цены  товара  никак  не  отразится  на  рыночной  ситуации.  Однако  это  не  верно,  поскольку  цена  товара  влияет  на  индекс  цены,  который  в  свою  очередь  связан  со  спросом  на  товар.  Фирма  не  осведомлена  о  спросе  на  ее  товар,  то  есть  она  воспринимает  его  как  случайную  величину  ,  q  —  это  оптимальный  спрос  на  товары,  а  ς  является  случайной  величиной  с  законом  распределения  .  Допустим,  что  случайная  величина  имеет  равномерное  распределение,  где  E(z)  =  1,    =  .  Далее  будет  показано,  как  введенный  в  модель  параметр  неопределенности  повлияет  на  поведение  потребителей  и  фирм  в  экономике. 

Оптимальный  спрос  на  товары  q(x)  определяется  путем  решения  задачи  потребителя  (подразумевается,  что  фирм  бесконечное  количество):

  ,  (11)

где  М  имеет  вид

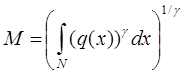    ,  (12)

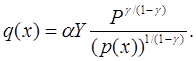    (13)

Поскольку  спрос  на  товар  зависит  от  его  цены,  то  фирма  должна  оптимизировать  цену  товара.  Могут  иметь  место  две  ситуации:  спрос  превышает  предложение  и  предложение  превышает  спрос.  Первая  из  них  может  произойти  с  вероятностью  .  Вторая  —  с  вероятностью    для  любого  значения  .  Учитывая  все  вышесказанное,  можно  записать  выражение  для  математического  ожидания  прибыли  фирмы,  которую  она  собирается  максимизировать:

  ,  (14) 

где    —  это  постоянные  издержки.  После  замены  переменных    выражение  (14)  примет  вид:

  .  (15)

Решением  данной  задачи  будет  являться  выражение

  .  (16)

Из  условия  свободного  входа  на  рынок 

  (17) 

можно  определить  равновесный  спрос  на  товары  q*,  цену  товаров  p*  и  зарплату  работников  w*:

    ,  (18)

  ,  (19)

    ,  (20)

где 

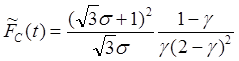    .  (21)

Для  определения  оптимального  количества  фирм  в  отрасли  будем  использовать  уравнение  баланса  денег:

    (22)

Принимая  во  внимание  (18)  и  факт,  что  ,  получим:

    (23)

Решение  задачи  потребителя  является  средним  значением  спроса  на  товар  фирмы  i.  Но  каким  же  образом  влияет  изменение  неопределенности  на  спрос?  При  увеличении  неопределенности  спрос  на  товар  уменьшается  вследствие  того,  что  спрос  имеет  обратную  зависимость  от  решения  задачи  фирмы  t,  где  t  имеет  прямую  зависимость  от  σ.  Зависимость  цены  товара  и  зарплаты  сотрудников  предприятий  отрасли  от  неопределенности  имеют  одинаковый  характер:  убывание  при    и  возрастание  при  ,  однако  заработная  плата  при  этом  растет  быстрее  цены  товара.  Как  было  выяснено  в  процессе  исследования,  значение  σ  никаким  образом  не  влияет  на  предложение  и  количество  фирм  в  отрасли.  В  принципе,  это  объяснимо:  предложение  контролируется  фирмой,  потому  что  она  его  и  создает. 

Выражаю  благодарность  моему  научному  руководителю  профессору  Шаповалу  А.Б.  за  помощь  в  написании  статьи.

Список  литературы:

1.Матвеенко  В.Д.  Модель  монополистической  конкуренции  Диксита-Стиглица:  межстрановая  версия  /  Экономическая  школа.  Альманах,  том  7,  2011.  Международная  экономика  /  отв.  ред.  А.П.  Киреев,  В.Д.  Матвеенко.  СПб.:  «Экономическая  школа»  ГУ  ВШЭ,  2011.  —  стр.  45—56.

2.Combes  P.-P.,  Mayer  T.,  Thisse  J.-F.  Economic  Geography  The  Integration  of  Regions  and  Nations.  Princeton  University  Press,  2008.  —  399  c.

3.Zhelobodko  E.,  Kokovin  S.,  Thisse  J.-F.  Monopolistic  Competition:  Beyond  the  CES,  PSE  Working  Papers  halshs-00566431,  2010.  —  40  с.