Статья опубликована в рамках: II Международной научно-практической конференции «Научное сообщество студентов: МЕЖДИСЦИПЛИНАРНЫЕ ИССЛЕДОВАНИЯ» (Россия, г. Новосибирск, 16 апреля 2012 г.)
Наука: Технические науки
Секция: Моделирование
Скачать книгу(-и): Часть I, Часть II, Часть III, Часть IV, Часть V
дипломов
ПРИМЕНЕНИЕ ПАКЕТА STATISTICA 6 ДЛЯ МОДЕЛИРОВАНИЯ И ПРОГНОЗИРОВАНИЯ КОЛИЧЕСТВА ЗВОНКОВ В ЦЕНТР ОБРАБОТКИ ВЫЗОВОВ
Пасмарнова Наталья Сергеевна
студентка 5 курса, кафедра прикладной математики ЛГТУ, г. Липецк
Кузнецова Елена Васильевна
научный руководитель, кандидат физико-математических наук, доцент, кафедра прикладной математики ЛГТУ, г. Липецк
В современном мире решение задач моделирования и управления востребовано повсеместно. Моделирование работы сервисной службы поддержки является актуальной проблемой для любой телекоммуникационной компании, так как согласование численности персонала и ресурсов поддержки с текущей рабочей нагрузкой критически важно для эффективного управления центрами операторской поддержки. Если точность прогноза недостаточна, то и весь остальной процесс планирования будет некорректен.
В связи с этим в данной работе рассматривается задача разработки математической модели, позволяющей адекватно строить прогноз количества звонков, ежедневно поступающих в центр обработки вызовов телекоммуникационной компании.
Одной из наиболее эффективных моделей для прогнозирования является модель АРПСС (p, d, q) (Ps, Ds, Qs) Бокса-Дженкинса. Параметрами АРПСС являются: p – порядок авторегрессии, d – порядок конечной разности, q – порядок скользящего среднего, Ps – сезонный параметр авторегрессии, Ds – сезонная конечная разность, Qs –сезонный параметр скользящего среднего[1, 3].
Модель АРПСС успешно применяется в решении похожих задач прогнозирования [2, 4, 5]. Поэтому в данной работе было решено использовать именно эту модель. АРПСС предлагается реализовать при помощи пакета статистического анализа STATISTICA 6.
Итак, приступим к построению модели. График исходного временного ряда представляет собой количество звонков, ежедневно поступающих в центр обработки вызовов. В работе использовались данные с апреля по сентябрь 2011 года. График представлен на рис.1.

Рис.1. График исходного временного ряда
Как можно заметить, на графике наблюдается несколько выбросов, которые обусловлены нерегулярной составляющей временного ряда. С помощью сезонной декомпозиции найдем случайную составляющую ряда. Она выглядит следующим образом:
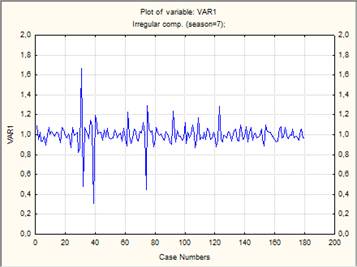
Рис. 2. Случайная составляющая временного ряда
Теперь получим очищенный ряд, вычитая из исходного ряда случайную составляющую. Преобразовав исходный ряд, построим модель АРПСС.
Для начала с помощью спектрального анализа Фурье определим сезонный лаг. Для этого построим график периодограммы.

Рис. 3. График периодограммы
На графике четко выделен пик в точке 7. Данный пик определяет основной период сезонной компоненты нашего ряда.
Далее исследуем автокорреляционную и частную автокорреляционную функцию очищенной переменной. Они показывают, что наш ряд не является стационарным.


Рис. 4. Графики автокорреляционной и частной автокорреляционной функции очищенного ряда
Также на полученных графиках ярко выражена сезонность с периодом 7.
Для того, чтобы приблизить ряд к стационарному, перейдем к первой разности нашего ряда (d=1)[3]. График преобразованного ряда представлен на рис.5.

Рис. 5. График преобразованного ряда
Теперь каждый член преобразованного ряда равен разностям между соседними членами очищенного ряда. Посмотрим на графики автокорреляционной и частной автокорреляционной функции данного ряда.


Рис. 6. Графики автокорреляционной и частной автокорреляционной функции преобразованного ряда
Как видно, после взятия разности исчезла корреляция не только на лаге 1, но и на большинстве остальных лагов, так как автокорреляции для последовательных лагов взаимозависимы.
Приведенные графики говорят о том, что наш ряд близок к стационарному, но у автокорреляции остались сезонные всплески с периодом, равным 7. Для того, чтобы удалить их, возьмем разность от переменной с первой разностью с лагом 7. После чего графики автокорреляционной и частной автокорреляционной функции будут выглядеть следующим образом:


Рис. 7. Графики автокорреляционной и частной автокорреляционной функции разности преобразованного ряда с лагом 7
Большая часть сильных автокорреляций теперь удалена. Хотя еще остались автокорреляции, большие 2-х стандартных ошибок, не следует брать еще разности ряда, т.к. они могут исключить эффект скользящего среднего.
Из графиков видно, что полученные преобразования свели наш ряд к близкому к стационарному ряду, и ряд готов для анализа с помощью АРПСС. Будем оценивать два параметра скользящего среднего модели АРПСС: один сезонный (Qs) и один несезонный (q). Параметры авторегрессии отсутствуют в модели. При таком количестве параметров в модели все переменные существенны. Это означает, что модель АРПСС (0,1,1), (0,1,1) пригодна для практического использования. Конечная модель представлена на рис.8.

Рис. 8. Оценки параметров полученной модели
После нахождения значимой модели можно построить прогноз на 7 последующих дней.

Рис. 9. График прогноза на 7 последующих дней
Как показывает график, построенная модель весьма разумно прогнозирует ряд.
На следующем этапе необходимо определить, насколько адекватно построена наша модель. Существует два стандартных метода анализа адекватности модели прогнозирования:
1. Визуальный анализ со сдвигом прогноза на несколько шагов назад. Приведем анализ прогноза со смещением на 7 дней назад.

Рис. 10. Визуальный анализ со сдвигом прогноза на 7 дней назад
Как видно, мы смогли достаточно точно определить значения.
2. Анализ остатков. Существует два предположения модели АРПСС:
1) остатки нормально распределены;
2) остатки независимы друг с другом, то есть между ними нет остаточной корреляции.
Предположение о нормальности остатков может быть проверено с помощью гистограммы остатков. Как можно заметить из рис.11, гистограмма подтверждает предположение о нормальности остатков.

Рис. 11. Гистограмма остатков
Далее проанализируем выполнение второго предположения АРПСС - остатки независимы друг от друга. Это можно проверить с помощью графика автокорреляционной и частной автокорреляционной функции.
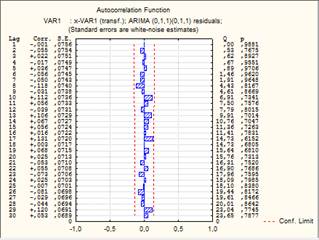

Рис. 12. График автокорреляционной и частной автокорреляционной функции
Из графиков видно, что остатки не коррелированны друг с другом.
Полученные результаты подтверждают адекватность использования построенной модели. Значит, модель АРПСС с параметрами p=0, d=1, q=1, Ps=0, Ds=1, Qs=1 пригодна для прогнозирования звонков, поступающих в центр обработки вызовов.
Список литературы:
1. Айвазян С. А., Мхитарян В. С. Прикладная статистика и основы эконометрики: учебник для вузов. – М.: ЮНИТИ, 1998. – 1022 с.
2. Большаков П. С. Прогнозирование индекса реального объема сельскохозяйственного производства в Российской Федерации в системе STATISTICA 6 / StatSoft Russia Technical support department. [Электронный ресурс] – Режим доступа. - URL:
http://www.statsoft.ru/home/portal/applications/ForecastingAdvisor/Examples/Example2.htm
3. Боровиков В. П. Прогнозирование в системе STATISTICA в среде Windows. Основы теории и интенсивная практика на компьютере: учеб. пособие. – М.: Финансы и статистика, 2000. – 384 с.
4. Исследование данных об авиаперевозках / StatSoft Russia. [Электронный ресурс] – Режим доступа. - URL: http://www.statsoft.ru/statportal/tabID__71/MId__330/ModeID__0/PageID__99/DesktopDefault.aspx
5. Семенчин Е. А., Чулков Д. В. Моделирование запаса товаров дистрибьютерских фирм (на примере ООО «Реликт», г. Краснодар) // Вестник Саратовского госагроуниверситета им. Н. И. Вавилова. – 2011. - №2. – С. 91-95
дипломов


Оставить комментарий