ПОЛУЧЕНИЕ ОБЩЕГО УРАВНЕНИЯ ДИНАМИКИ ГАЗОГЕНЕРАТОРА

Дронь Михаил Михайлович

студент 2 курса магистратуры, кафедра АВиРС ОмГТУ, г. Омск

Е-mail: u1TRo@mail.ru

Яковлев Алексей Борисович

научный руководитель, канд. техн. наук, доцент ОмГТУ, г. Омск

Жидкостная ракетная двигательная установка (ЖРДУ) является сложной технической системой, составляющим элементам которой присущ динамический характер протекающих в них процессов. Элементы ЖРДУ (камера, магистрали, турбонасосный агрегат, газогенератор и др.) сами по себе являются сложными динамическими звеньями, имеющими сложные связи между собой. В связи с этим при проектировании ЖРДУ необходимо уметь анализировать ее динамические свойства и свойства составляющих ее агрегатов с целью создавать отдельные узлы и двигательную установку в целом с заданными динамическими характеристиками [1, с. 15].

Таким образом, целью данной работы было получение общего уравнения динамики одного из элементов ЖРДУ с насосной системой подачи, а именно, однокомпонентного газогенератора (ГГ) и анализ его динамических свойств. Для этого было необходимо:

·провести декомпозицию ГГ на отдельные составляющие его элементы;

·получить уравнения динамики этих элементов;

·вскрыть внутренние связи элементов, составляющих ГГ, и получить его структурную схему;

·записать уравнение динамики ГГ и привести его к типовому виду;

·проанализировать основные динамические свойства ГГ.

Динамическая характеристика объекта регулирования (ОР) — это зависимость выходной величины ОР, выраженная аналитически или графически, от времени при изменении входных величин и действующих на ОР возмущений. ОР может быть часть какой-либо системы или целая система. Но и один объект может быть объектом сразу нескольких САУ [2, с. 354].

В данном случае ОР является газогенератор (ГГ), выполненный в виде системы, состоящей из камеры разложения, форсуночной головки и дроссельного крана, установленного на входе в ГГ. Для упрощения задачи сопротивления форсуночной головки ГГ и пакета катализатора объедине­ны и рассматриваются как единый элемент с сосредоточенным сопротивлением.

Запишем уравнения динамики элементов системы.

1.  Камера разложения

где:  — постоянная времени камеры разложения;

 — безразмерное отклонение давления топлива;

 — безразмерное отклонение расхода в ГГ [3, с. 78].

Переходный процесс соответствует уравнению динамики инерционного звена.

2.  Форсуночная головка

где:  — коэффи­циенты усиления;

 — отклонение давления в форсуночной головке ГГ. Переходный процесс соответствует уравнению динамики усилительного звена [1, с. 115].

В этом выражении, коэффициент K₆ характеризует сво­ей величиной степень самовыравнивания процесса подачи расхода в камеру разложения с одновременным ее опорожнением. Величина этого коэффициента определя­ется из соответствующего выражения как уровнем режима, так и тангенсом угла наклона касательной к кривой (частной производной) связи расхода при постоянном давлении перед форсункой с давлением в камере разложения в точке номинального режима.

3.  Дроссельный кран

где:  — коэффи­циенты усиления;

 — отклонение давления в баке;

 — относительная площадь открытия дроссельного крана [3, с. 80].

Поскольку данное уравнение динамики соответствует свойствам идеального усилительного звена по отношению к каждому из входов, то и переходные процессы воспроизводят на выходе форму входного сигнала без искажения, деформируя лишь его ординату.

Составим систему уравнений для описания объекта регулирования:

Можно сказать, что решением системы будет являться уравнение первого порядка, т. к. уравнения динамики форсуночной головки и дроссельного крана имеют нулевой порядок, а камера разложения имеет первый порядок дифференцирования по времени. Решая последовательно данную систему, получим:

.

Данное уравнение является общим уравнением динамики газогенератора и имеет следующие коэффициенты усиления и постоянную времени:

По своим свойствам это уравнение первого порядка и соответствует уравнению динамики инерционного звена.

Переходная характеристика этого звена представляет собой экспоненциальную зависимость вида

где:  — входные воздействия.

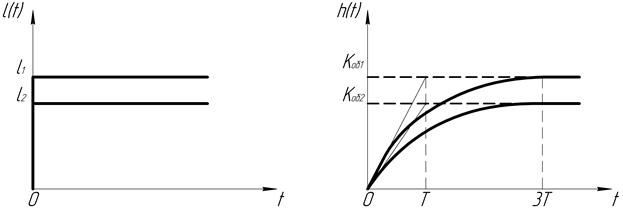
Рисунок 1. Переходная характеристика инерционного звена

Полученное уравнение существенно упрощает структурную схему САУ, делая её не такой громоздкой и сложной (рис. 2).

Рисунок 2. Структурная схема газогенератора

Из общего уравнения газогенератора можно увидеть, что для нахождения выходной величины — , достаточно знать только две входные величины —  и , а так же конструктивные параметры и зависимости от времени давления и расхода рабочего тела. Полученное уравнение так же отражает наполнение (или расходование) газа с учетом его сжимаемости, что подтверждает свойство инерционности, но оно не учитывает запаздывание разложения (воспламенения) топлива. Данное свойство может быть учтено введением в ОР дополнительного звена с чистым (постоянным) запаздыванием.

Список литературы:

1.  Бабкин А.И. и др. Основы теории автоматического управления ракетных двигательных установок. — М.: Машиностроение, 1986. — 456 с.

2.  Попов Е.П. Теория линейных систем автоматического регулирования и управления. — М.: Наука, 1978. — 800 с.

3.  Яковлев А.Б. Уравнения динамики двигательной установки. — Омск: Изд-во ОмГТУ, 1999. — 88 с.