Статья опубликована в рамках: XI Международной научно-практической конференции «Научное сообщество студентов XXI столетия. ТЕХНИЧЕСКИЕ НАУКИ» (Россия, г. Новосибирск, 06 мая 2013 г.)
Наука: Технические науки
Секция: Архитектура, Строительство
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
ИССЛЕДОВАНИЕ ПРОСТРАНСТВА ЗНАЧЕНИЙ НАПРЯЖЕННО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ ПОЛОГИХ ГЕОМЕТРИЧЕСКИ-НЕЛИНЕЙНЫХ ОБОЛОЧЕК ВРАЩЕНИЯ ПРИ РАЗЛИЧНЫХ ЗНАЧЕНИЯХ ГЕОМЕТРИЧЕСКИХ ПАРАМЕТРОВ, УСЛОВИЙ ЗАКРЕПЛЕНИЯ
Никулина Мария Владимировна
магистрант, кафедра городского, дорожного строительства и строительной механики, ЮЗГУ, г. Курск
Никитин Константин Евгеньевич
научный руководитель, канд. техн. наук, доцент, ЮЗГУ, г. Курск
Исследовано влияние различных параметров пологих геометрически-нелинейных оболочек вращения на ее напряженно-деформированное состояние. Определены границы изменения параметров оболочки, в рамках которых нельзя пренебречь влиянием геометрической нелинейности.
Ключевые слова: пологие оболочки вращения, геометрически нелинейная теория оболочек
Целью настоящего исследования было изучение геометрических параметров, характеристик материала, условий закрепления пологих оболочек вращения, на возникающее в них напряженно-деформированное состояние. Рассматриваются характерные закономерности распределения усилий, напряжений и перемещений в оболочке вдоль образующей оболочки. Отыскиваются сочетания параметров оболочки, при которых происходит качественное изменение этих закономерностей, появление на них экстремальных значений. По результатам исследования ведется поиск рациональных значений параметров оболочки.
Оболочка рассматривается как в рамках геометрически нелинейной теории, так и в рамках линейной теории оболочек. Рассматриваются характерные закономерности распределения усилий, напряжений и перемещений в оболочке вдоль образующей оболочки. Отыскиваются сочетания параметров оболочки, при которых происходит качественное изменение этих закономерностей, появление на них экстремальных значений.
В данной работе рассматриваются тонкие пологие оболочки, для которых применимы гипотезы Киргофа-Лява. Полагаем, что материал оболочки однородный и подчиняется закону Гука.
Уравнения пологих оболочек сформулированы в смешанном виде и выражены в безразмерных функциях усилий и углов поворота образующей оболочки. Граничные условия на опорном контуре представлены в виде упруго-податливой заделки. Геометрическая нелинейность рассматривается в рамках квадратично-нелинейной теории пологих оболочек [3].
Рассмотрен класс пологих оболочек, имеющих гладкую поверхность вращения произвольного вида. Считаем, что на оболочку действует вертикальная осесимметричная нагрузка, распределенная по произвольному закону. Следовательно, значения всех усилий, моментов, перемещений и деформаций в точках, расположенных на одной параллели будут одинаковы.
В качестве искомых величин, выступают безразмерные функции напряжений ![]() (фи) и углов поворота образующей
(фи) и углов поворота образующей ![]() (тэта).
(тэта).
Уравнения для их определения приняты в виде:
 ;
;
 ,
,
где: ![]() — безразмерная радиальная координата;
— безразмерная радиальная координата;
![]() — безразмерная функция, пропорциональная производной от функции образующей оболочки по координате
— безразмерная функция, пропорциональная производной от функции образующей оболочки по координате ![]() ;
;
![]() ;
;
![]() ,
, ![]() — константы интегрирования, величина которых зависит от граничных условий;
— константы интегрирования, величина которых зависит от граничных условий;
E — модуль упругости материала.
Константы интегрирования зависят от граничных условий в центре оболочки и равны:
![]() ;
; 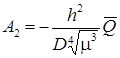 .
.
Уравнения для определения усилий через ![]() и
и ![]() :
:
 ;
; 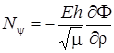 ;
;  ;
;  .
.
 ;
; 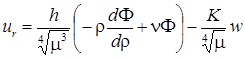
Положительные направления усилий и моментов, действующих на элемент оболочки приведены на рис. 1.
Граничные условия для упругоподатливой опоры сформулированы используя предположение о том, что изгибающие моменты и продольные усилия на контуре пропорциональны соответственно углу поворота контура и радиальному перемещению ur [2], т. е.

где: k1 и k2 — коэффициенты пропорциональности, характеризующие жесткость опорного контура в отношении поворота и радиального перемещения. Кроме того, будем предполагать, что в опоре вертикальное перемещение w = 0.

Рисунок 1. Положительные направления усилий и моментов, действующих на элемент оболочки
Граничные условия в центре замкнутой в вершине оболочки имеют вид: θ = 0; Φ = 0, α = 0.
Граничные условия на опоре:
 ;
;
 ,
,
где: m — параметр условий закрепления оболочки в отношении поворота, варьируется в пределах от ![]() до
до ![]() , где:
, где:
![]() — коэффициент Пуассона;
— коэффициент Пуассона;
n — параметр характеризующий податливость опорного контура радиального смещения, варьируется в пределах от![]() до
до![]() .
.
В качестве объекта исследования выступает замкнутая в вершине пологая оболочка вращения с образующей, заданной функцией
![]()
где: fmax — стрела подъема по центру оболочки;
ρ — новая безразмерная координата, меняющая значения от 0 в центре оболочки до 1 на краю;
Z — параметр формы образующей оболочки;
Для решения задачи определения напряженно-деформированного состояния используется метод Бубнова-Галеркина в смешанной конечно-элементной формулировке [4].
Исследование напряженно-деформированного состояния осуществляется последовательным перебором значений геометрических параметров оболочки: радиуса основания оболочки a, стрелы подъема по центру оболочки fmax, параметра формы образующей оболочки Z, толщины оболочки h, модуля упругости материала оболочки Е, параметров закрепления оболочки m и n. Для каждого фиксированного набора значений вышеуказанных параметров строились графики распределения усилий, перемещений и напряжений вдоль образующей. Определялась относительная разница между линейными и нелинейными решениями в экстремальных точках. В качестве порога, при котором влияние геометрической нелинейности считалось значительным, было выбрано отклонение от линейного решения более чем на 5 %.
На настоящий момент, в результате проведенных исследований был определен диапазон изменения параметров, при которых влияние геометрической нелинейности незначительно при приложении осесимметричной равномерно распределенной нагрузки интенсивностью ![]() и
и ![]() . При значениях радиуса оболочки а в пределах от 0,1 до 0,73 м, при значениях стрелы подъема оболочки fmax от 0,1 до 1 м. С увеличением толщины оболочки разница между линейным и нелинейным решениями уменьшается. Для усилий
. При значениях радиуса оболочки а в пределах от 0,1 до 0,73 м, при значениях стрелы подъема оболочки fmax от 0,1 до 1 м. С увеличением толщины оболочки разница между линейным и нелинейным решениями уменьшается. Для усилий ![]() и
и ![]() пороговой является величина в 7 мм. При значениях параметра
пороговой является величина в 7 мм. При значениях параметра ![]() разница существенна и превышает значение в 5 %. Для прогибов справедливо следующее утверждение: при толщине оболочки
разница существенна и превышает значение в 5 %. Для прогибов справедливо следующее утверждение: при толщине оболочки ![]() влияние геометрической нелинейности незначительно, с уменьшением толщины при расчетах оболочек необходимо учитывать нелинейность.
влияние геометрической нелинейности незначительно, с уменьшением толщины при расчетах оболочек необходимо учитывать нелинейность.
Список литературы:
1.Валишвили Н.В. Методы расчета оболочек вращения на ЭЦВМ. — М.: Машиностроение, 1976. — 278 с.
2.Гениев Г.А., Чаусов Н.С. Некоторые вопросы нелинейной теории устойчивости пологих металлических оболочек.// Научное сообщение.
3.Григолюк Э.И., Мамай В.И. Нелинейное деформирование тонкостенных конструкций. — М.:Наука. Физматлит, 1997. — 272 с.
4.Никитин К.Е. Численное исследование задач статики и динамики пологих геометрически нелинейных изотропных и ортотропных оболочек вращения на основе смешанного метода: Дис. канд. технических наук. Курск. 2006. — 150 с.
дипломов


Оставить комментарий