Статья опубликована в рамках: XI Международной научно-практической конференции «Научное сообщество студентов XXI столетия. ТЕХНИЧЕСКИЕ НАУКИ» (Россия, г. Новосибирск, 06 мая 2013 г.)
Наука: Технические науки
Секция: Энергетика
Скачать книгу(-и): Сборник статей конференции
- Условия публикаций
- Все статьи конференции
дипломов
ВЫБОР НАЧАЛЬНЫХ ПРИБЛИЖЕНИЙ ДЛЯ РАСЧЕТА ДОПУСТИМЫХ ПО СТАТИЧЕСКОЙ УСТОЙЧИВОСТИ РЕЖИМОВ ЭЛЕКТРОЭНЕРГЕТИЧЕСКОЙ СИСТЕМЫ
Годяцкая Екатерина Андреевна
студент 2 курса магистратуры, кафедра «Электроснабжение и электротехника» ИЭиЭ ТГУ, г. о. Тольятти
E-mail: g.katrin@inbox.ru
Карташева Ксения Вячеславовна
студент 2 курса магистратуры, кафедра «Информатика и вычислительная техника» ИМФиИТ ТГУ, г. о. Тольятти
E-mail: KartashevaK.V@yandex.ru
Сенько Владислав Владимирович
научный руководитель, канд. техн. наук, доцент ТГУ, г. Тольятти
Благодаря широкому внедрению в электроэнергетику современных информационно-вычислительных систем для решения задач диспетчерского и противоаварийного управления возросла актуальность вопросов, связанных с моделированием допустимых по статической апериодической устойчивости (САУ) режимов электрических систем. При этом важным требованием надежности функционирования электроэнергетических систем (ЭЭС) является обеспечение нормативного запаса САУ, который характеризует допустимость режима.
Установившиеся режимы электроэнергетических систем (ЭЭС) описываются нелинейными уравнениями вида:
![]() , (1)
, (1)
где: ![]() — n-мерная вектор-функция, отвечающая равнениям баланса мощностей или токов в узлах сети;
— n-мерная вектор-функция, отвечающая равнениям баланса мощностей или токов в узлах сети;
![]() — заданный вектор регулируемых параметров;
— заданный вектор регулируемых параметров;
![]() — искомый вектор нерегулируемых параметров.
— искомый вектор нерегулируемых параметров.
Активные и реактивные мощности генераторов нагрузок принимаются в качестве регулируемых параметров. При этом действительные и мнимые составляющие или модули фазы узловых напряжений являются зависимыми параметрами.
Предельные по САУ режимы определяются уравнениями (1) и условием:
![]() , (2)
, (2)
где: ![]() — матрица, отвечающая свободному члену a0 характеристического полинома:
— матрица, отвечающая свободному члену a0 характеристического полинома:
![]()
Системы дифференциальных уравнений:
![]()
описывающих переходные процессы в ЭЭС при малых возмущениях.
При определенных условиях свободный член a0 может практически совпадать с якобианом уравнений установившегося режима, поэтому можно считать, что предельные по устойчивости режимы будут соответствовать точкам Хпр, Yпр пространства параметров ![]() , в которых выполняются уравнения (1) и условие:
, в которых выполняются уравнения (1) и условие:
![]() (3)
(3)
Точки Yпр в пространстве Y образуют гиперповерхность LY.
Представление о запасе устойчивости (3) можно получить, сопоставляя в пространстве регулируемых параметров положение точки используемого режима Y0 относительно границы LY области устойчивых режимов [1, 3].
Математически задачу оценки запаса можно сформулировать следующим образом. Определить
![]() (4)
(4)
При ограничениях:
![]() (5)
(5)
где: Y0 — значение вектора регулируемых параметров в режиме, для которого определяется запас;
DY — вектор приращений переменных Y0, обеспечивающих «вывод» режима на гиперповерхности LY.
Для решения сформулированной задачи запишем функцию Лагранжа:
![]() (6)
(6)
где: h — вектор неопределенных множителей.
Минимуму L соответствуют условия:
 (7)
(7)
Последняя система имеет 2 решения:
1. Тривиальное, которое отвечает исходному режиму с параметрами х0, у0. В этом случае ![]() .
.
2. Искомое, когда хотя бы одна из компонентов векторов ![]() и DY
и DY
Для отсечения тривиальных значений необходим специальный выбор начальных приближений вблизи предельной поверхности.
Преобразовав систему (7) получаем:
 (8)
(8)
В работе [2] показана модификация уравнений (8) в виде системы (9) для определения допустимого режима, отвечающего требуемому запасу устойчивости ЗT, как при известном направлении утяжеления ΔY, так и в наиболее опасном. В результате были получены обобщенные уравнений предельных режимов (ОУПР):
 (9)
(9)
После определения Xпр, Yпр и Т параметры Y0 находятся из соотношения (9), а XД — из решения уравнений:
![]()
Система уравнений (9) решалась методом Ньютона, где искомыми параметрами являлись векторы X, R и скалярный вектор Т.
Авторами разработана экспериментальная программа «Energy-VB» (с использованием платформы программирования VB.NET), которая позволяет строить границы области устойчивости и допустимой области для тестовой схемы ЭЭС (рис. 1), используя описанные выше алгоритмы.
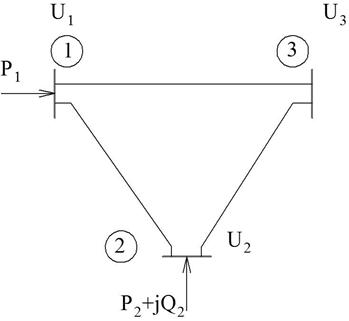
Рисунок 1. Трехузловая модель ЭЭС
С помощью данной программы проводились расчеты для трех различных направлений утяжеления (рис. 2). Результаты показали, что искомые допустимые точки Yдi и соответствующие им точки предельной поверхности Yпрi определяются за семь итераций. Детальные результаты, отражающие ход вычислительного процесса утяжеления отражены на рис. 3—5. При анализе этих результатов видно, что на первых трех итерациях доминирующими являются второе и третье уравнения системы (9).

Рисунок 2. Результаты определения допустимых режимов в координатах Y1, Y2
Действительно, на первых трех итерациях длина вектора невязок
![]() резко убывает (рис. 3), тогда как невязки уравнений режима
резко убывает (рис. 3), тогда как невязки уравнений режима ![]() возрастают (рис. 2).
возрастают (рис. 2).

Рисунок 3. Изменение невязок ![]() на итерациях
на итерациях

Рисунок 4. Изменение невязок ![]() и
и ![]() на итерациях
на итерациях
Данные итерации соответствуют первому этапу вычислений — «выстреливанию» в направлении предельной поверхности. В ходе этого процесса изменяются невязки ![]() ,
, ![]() ,
, ![]() , что сопровождается уточнением параметра Т и вектора
, что сопровождается уточнением параметра Т и вектора ![]() (рис. 4).
(рис. 4).
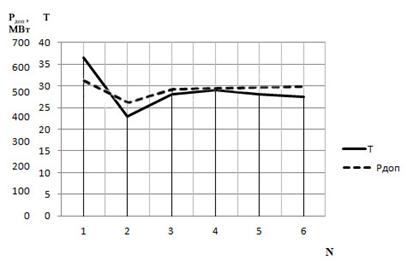
Рисунок 5. Изменение параметра Т и величины вектора Y0+T∆Y — M-2R на итерациях при решении системы уравнений
При решении задач оперативного управления в условиях полного использования пропускной способности основных связей выбор начальных приближений, как правило, не вызывает затруднений.
Однако выбор начальных приближений для вектора R является более сложным. При неудачном выборе начальных приближений возможен поворот вектора R в противоположную сторону и выход Yдi за границу предельных режимов LY. Поэтому необходимо следить на итерациях за изменением знака R и при выходе Yдi за границу LY менять знак R0 на противоположный.
Предложенные авторами методики и вычислительные алгоритмы позволяют определять параметры Xпр, Yпр предельного по устойчивости режима в заданном направлении утяжеления DY и в критическом направлении утяжеления. Так же производить расчет параметров Xдоп, Yдоп допустиого режима, соответствующего требуемому запасу устойчивости.
Методика определения допустимых режимов на основе ОУПР позволят повысить скорость принятия решений в задачах оперативного управления ЭЭС, снизить ущерб при отключении генераторов и нагрузок при проведении режимных ограничений потребителей.
Список литературы:
1.Веников В.А., Строев В.А., Виноградов А.А., Идельчик В.И. Расчет запаса статической устойчивости электроэнергетической системы // Изв. АН СССР. Энергетика и транспорт. — № 3. — 1984.
2.Крюков А.В. Предельные режимы электроэнергетических систем // ИрГУПС — Иркутск, 2012. — 236 с.
3.Крюков А..В., Сенько В.В. Определение допустимых режимов и оценка запасов устойчивости энергосистем // В сб. Проблемы развития электроэнергетических систем / материалы науч.- тех. Конференции молодых ученых и специалистов, — СПбГТУ. СПб. 1992. С. 29—32.
дипломов


Оставить комментарий