ПОСТАНОВКА ОПТИМИЗАЦИОННОЙ ЗАДАЧИ РАСКРЯЖЕВКИ ФАУТНЫХ ХЛЫСТОВ

Сурикова Мария Александровна

студент 5 курса, кафедра АПП ВГЛТА, РФ, г. Воронеж

E-mail:

Хухрянская Елена Станиславовна

научный руководитель, канд. техн. наук, доцент ВГЛТА, РФ, г. Воронеж

Каждое лесозаготовительное предприятие наряду с объемными показателями производства лесоматериалов имеет сортиментный план, который составляется с учетом лесосечного фонда и заявок потребителей и является законом для производственной деятельности предприятия. Основой наиболее эффективной эксплуатации лесных ресурсов является следующее: наиболее полное использование лесосечного фонда без технической порчи при лесозаготовках; получение наибольшего количества деловых сортиментов в общем выходе лесоматериалов, т. е. тщательное отделение деловой древесины от дров; постоянная работа по повышению сортности и качества заготовляемых деловых сортиментов, т. е. получение наиболее ценных лесоматериалов [3].

Каждый хлыст имеет свои особенности. Поэтому для осуществления рациональной заготовки древесины необходима индивидуальная разметка и раскряжевка каждого хлыста с учетом его диаметра, длины, сбега, а также наличия, расположения и размеров пороков древесины. Основное в работе оператора полуавтоматической линии, разметчика, раскряжевщика — полное использование каждого хлыста, максимальное снижение потерь древесины при раскряжевке, получение наибольшего выхода деловой древесины наивысшего качества [1]. Для успешного решения стоящих перед ними задач указанные работники обязаны хорошо знать: сортиментный план, действующие стандарты на производимые лесоматериалы; пороки древесины способы их измерения и закономерности проявления в хлыстах, отпускные цены на заготавливаемые сортименты; основные правила и приемы рационального раскроя хлыстов различных пород.

Раскряжевку хлыстов начинают с комля. Это относится, прежде всего, к здоровым стволам, а также к таким фаутным стволам, на которых размеры пороков и характер их распространения могут быть определены путем осмотра. Когда распространение порока по стволу определить затруднительно, раскряжевку необходимо начинать с наиболее пораженного участка чтобы лучше вскрыть влияние порока на выход сортиментов.

Каждый хлыст должен быть раскроен оптимально. Степень оптимальности раскроя определяется критериями [6]. Критерий оптимальности раскряжевки — это технико-экономический показатель раскроя, характеризующий количественный и качественный выход продукции. В теории и практике раскроя хлыстов используют следующие критерии оптимальности: объемный выход деловых сортиментов, спецификационный выход сортиментов, выход цилиндрического объема, объемный выход спецификационных пиломатериалов или заготовок.

Остановимся на одном из критериев оценки эффективности раскроя хлыстов — выходе цилиндрического объема сортиментов [5]. В работах [5, 6] была использована процедура отыскания размеров определенного количества отрезков хлыста, описываемого математически его образующей d = d(x) — зависимостью диаметра d от расстояния x вдоль оси хлыста, заданной на интервале [a, b]. Данная аналитическая зависимость получена эмпирически для основных промышленных пород [4].

Остановимся на модели раскряжевки здорового хлыста, чтобы затем обобщить ее. Рассмотрим функцию f(x) = 0,25pd²(x), которая представляет собой площадь сечения хлыста на некотором расстоянии x от его вершины (или комля) (рис. 1). Если заданы координаты некоторого сортимента хлыста x_i-1 и x_i, тогда произведение (x_i-x_i-1)f(x_i-1), т. е. площадь ступеньки под функцией f(x), будет равно цилиндрическому объему соответствующего сортимента. Очевидно, что лучший в смысле максимума цилиндрического выхода раскрой хлыста на n сортиментов будет обеспечен выбором n-1 расстояний вдоль хлыста (узлов) таких, чтобы площадь под ступенчатой функцией (рис. 1) оказалась максимальной.

Рисунок 1. Пояснение к модели раскряжевки

Площадь под ступенчатой функцией, расположенной под кривой f(x), представляет собой, в свою очередь, функцию n-1 переменных x₁, ..., x_n-1, непрерывную на интервале [a, b], принимающую минимальные значения при x₁= ...= x_n-1 = a и x₁ =... = x_n-1 = b, и имеющую максимум при a < x₁ <...< x_n-1 < b. Следовательно, условием максимума площади

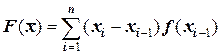                       (1)

под ступенчатой функцией является равенство

                           (2)

Дифференцируя (1), получим

                         (3)

Поскольку абсцисса начального узла x₀ = a известна и соответственно известно значение функции в этом узле f(x₀) = f(a), то если некоторое заданное значение очередной абсциссы x₁ обеспечит в соответствии с (3) в конечном итоге вычислений всех x_i (" i = 1, ..., n) значение x_n = b , то задача решена. Если же окажется, что x_n > b или x_n < b, то соответственно и значение абсциссы x₁, необходимое для выполнения условий максимума площади под ступенчатой функцией, либо завышено, либо занижено. Эти математические выкладки позволяют построить простой итерационный алгоритм, последовательно уточняющий некоторое произвольно заданное значение абсциссы x₁ до такого, которое обеспечит нахождение всех оставшихся узлов, удовлетворяющих условиям (2).

Отметим, что обычно в функции, определяющей образующую хлыста d = d(x), расстояние x отсчитывается от комлевого среза, что вполне допустимо и для применения данного алгоритма [2].

Предположим теперь, что хлыст имеет центральную гниль, образующая h = h(x) которой также известна. Обозначим g(x)=0.25ph²(x) — функцию, представляющую собой площадь сечения области гнили на расстоянии x от вершинного среза (рис. 2). Для решения задачи максимизации выхода цилиндрического объема деловой древесины n сортиментов, получаемых из хлыста с центральной гнилью, необходимо будет выбрать расположение n-1 узлов так, чтобы обеспечить максимум площади фигуры, образованной ступенчатыми функциями под кривой f(x) и над кривой g(x).

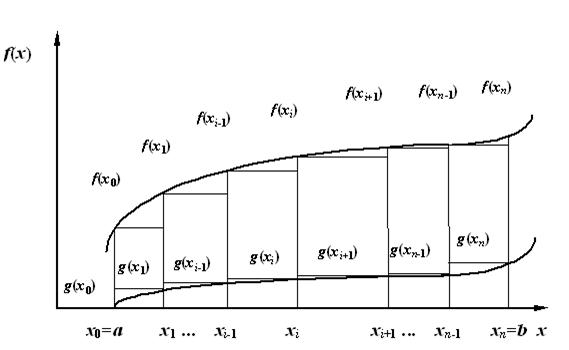
Рисунок 2. Модель раскряжевки при наличии центральной гнили

Площадь такой фигуры представляет собой функцию n-1 переменных x₁, ..., x_n-1, непрерывную на интервале [a,b], принимающую минимальные значения при x₁= ...= x_n-1 = a и x₁=... =x_n-1 = b и имеющую максимум при a < x₁ <...< x_n-1 < b. Условием максимума площади

            (4)

ступенчатой фигуры является равенство нулю частных производных

                           (5)

при граничных условиях

                (6)

Дифференцируя (4), получим

              (7)

Система (7) представляет собой систему n-1 нелинейных уравнений относительно x_i (i = 1,...n-1), каждое из которых представляет собой непрерывно дифференцируемую действительную функцию переменных x_i-1, x_i, x_i+1. Данную систему также можно численно решить методом Ньютона.

Отметим, что при численной реализации указанного алгоритма можно и необходимо учитывать то обстоятельство, что функция g(x) определена, как правило, не на всем интервале [a, b].

Итогом решения задачи максимизации выхода цилиндрического объема сортиментов при раскряжевке фаутного хлыста являются длины сортиментов, обеспечивающие максимум объема деловой древесины, заключенной в кольцевом цилиндре (без учета сбеговой части сортимента и центральной гнили), т.е. обеспечивающие максимум выхода пиломатериалов.

Список литературы:

1.Болдырев В.С. Технологические основы раскроя сырья и пиломатериалов: Учеб. пособие. Воронеж: Воронеж. Гос. лесотехн. акад., 2002. — 366 с.

2.Болдырев В.С., Лимонов Е.А., Хухрянская Е.С. К вопросу оптимизации раскряжевки древесных хлыстов мягких лиственных пород//Актуальные проблемы анализа и обеспечения надежности и каче­ства приборов, устройств и систем: Тез. докл. Междунар. науч.-техн. конф. Пенза: ПГТУ, 1998. — С. 163.

3.Редькин А.К. Математическое моделирование и оптимизация технологий лесозаготовок / А.К. Редькин, С.Б. Якимович М.: Изд-во МГУЛ, 2005 — 503 с.

4.Петровский В.С. Оптимальная раскряжевка лесоматериалов. 2-е изд., перераб. и доп. М.: Лесн. пром-сть, 1989. — 288 с.

5.Червинский В.А. Методы максимизации выхода цилиндрического объема сортиментов при раскряжевке древесных хлыстов// Изв. вузов. Лесн. журн. — 1978. — № 3. — С. 113—117.

6.            Червинский В.А. Раскрой древесных хлыстов. Воронеж: Изд-во ВГУ, 1982. — 64 с.