Статья опубликована в рамках: XLIV Международной научно-практической конференции «Научное сообщество студентов XXI столетия. ТЕХНИЧЕСКИЕ НАУКИ» (Россия, г. Новосибирск, 26 июля 2016 г.)
Наука: Технические науки
Секция: Телекоммуникации
Скачать книгу(-и): Сборник статей конференции
дипломов
РЕШЕНИЕ ЗАДАЧИ ЧАСТОТНОГО ПЛАНИРОВАНИЯ MESH СЕТЕЙ
Введение
Стремительное развитие беспроводных технологий, привели к появлению стандартов беспроводной связи, таких как LTE , WI-MAX, 5G, 802.11ac, каждое новое поколение стандартов беспроводной связи увеличивает скорость передачи информации на порядок, в связи, с чем увеличивается количество пользователей беспроводных сетей. Большие скорости передачи, позволяют использовать беспроводные технологии, не только как метод доступа, но и как способ соединения коммутационных узлов. Сети, где организация связи происходит с помощью какого-либо беспроводного стандарта связи называют Mesh, ad-hoc сети. Одной из основных проблем при планировании Mesh сетей является проблема выбора частот, на которых будут взаимодействовать узлы Mesh сети между собой, данным вопросам посвящены, например, такие статей как [1-5], в этих и других статьях как правило описываются алгоритмы ориентированные на Mesh сети работающие по стандарту 802.11 или 802.16. В данной статье предлагается разработка алгоритма позволяющего получить распределение частот не привязываясь к какому-либо стандарту, а учитывая что в Mesh сети будет использоваться полнодуплексная связь с частотным разделением каналов между собой.
Постановка задачи
Пусть Mesh сеть состоит из N узлов-радиостанций (далее РС) с координатами (Xi, Yi) i ∈ 1..N, каждая РСi имеет всенаправленную антенну, c радиусом действия Ri, необходимо определить ширину канала связи Δfij j ∈ 1..N между каждой парой PC, при условии, что общий выделяемый диапазон частот располагается от Fниж до Fверх.
Решение задачи
Для наглядности параллельно будем рассматривать пример со следующими исходными данными.
Координаты радиостанций:
РС1 (4;4), радиусом распространения сигнала R1 = 3 км;
РС2 (6;5), радиусом распространения сигнала R2 = 5 км;
РС3 (9;8), радиусом распространения сигнала R3 = 8 км;
РС4 (9;10), радиусом распространения сигнала R4 = 3 км;
РС5 (14;6), радиусом распространения сигнала R5 = 3 км;
РС6 (18;17), радиусом распространения сигнала R6 = 3 км;
РС7 (16;5), радиусом распространения сигнала R7 = 11 км.
Выделенный частотный диапазон F (3500..3611) МГц. Минимальный частотный диапазон канала 1 МГц. Защитный интервал между двумя соседними частотными каналами равно 0.1 МГц.
Схематичное изображение:
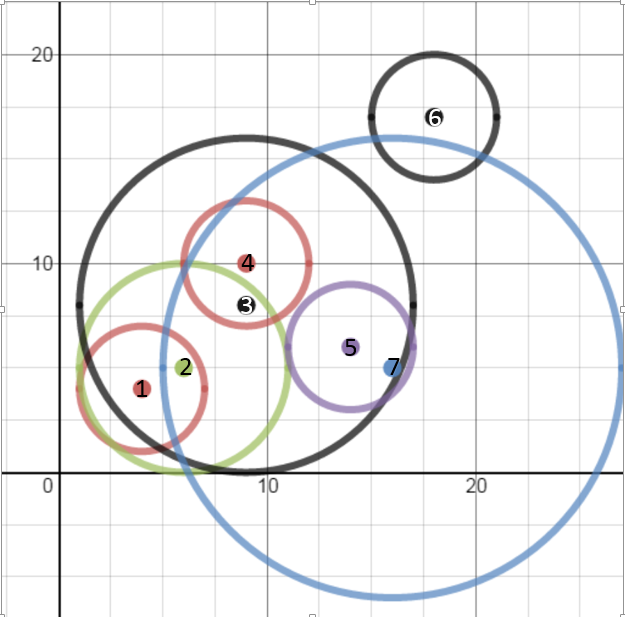
Рисунок 1. Топология Mesh сети
Зная координаты каждой РС, рассчитаем расстояния от передающей РС до всех остальных РС, путем вычисления корня суммы квадратов разности одноименных координат:
 , далее расстояние от РСi к РСj будем обозначать Lij .
, далее расстояние от РСi к РСj будем обозначать Lij .
Пример:
По ходу решения каждую РС будем рассматривать как передающую РС и принимающую РС.
Рассчитаем расстояния от РС1 до РС2-РС7:
РС1–РС2= L12 =  2.236 км;
2.236 км;
РС1-РС3 = L13 = 6.403 км;
РС1-РС4 = L14 = 7.81 км;
РС1-РС5 = L15 = 10.198 км;
РС1-РС6 = L16 = 19.105 км;
РС1-РС7 = L17 = 12.042 км.
Рассчитаем расстояние аналогично и для других РС.
Далее составим матрицу приема-передачи «А» размера  , где главная диагональ равна нулю, номер строки является номером передающей станции. Сравниваем Lij c Ri , если
, где главная диагональ равна нулю, номер строки является номером передающей станции. Сравниваем Lij c Ri , если  , то РС входит в поле распространения сигнала передающей РС и в матрице приема-передачи ставится единица, иначе ноль.
, то РС входит в поле распространения сигнала передающей РС и в матрице приема-передачи ставится единица, иначе ноль.

Пример:
Матрица приема-передачи для исследуемой сети:

Оптимизируем матрицу приема-передачи. Если i–ая строка не имеет ни одной единицы и i–ый столбец не имеет ни одной единицы, то это означает, что РС под номером i, не входит ни в чьё поле распространения волны, и в поле распространения волны i–ой РС ни одна РС не входит (РС i–ая изолированная). В таком случае убираем и столбец, и строку под номером i в матрице приема-передачи.
Пример:

Составляем матрицу взаимных сигналов «В» из матрицы приема-передачи. Выпишем из матрицы приема-передачи, все элементы равные единице, причем элемент равные единице будем обозначать fij, где i– это номер строки, а j – это номер столбца. Составим матрицу взаимных сигналов
 , где главная диагональ равна нулю, номер строки и столбца является fij.
, где главная диагональ равна нулю, номер строки и столбца является fij.Пример:

Выбираем в матрице приема-сигнала (А) элемент с номером строки i и номером столбца j. Выделяем строку i, столбцы i и j. Если в i и j столбцах есть единичные элементы, то они выделяются вместе с соответствующей строкой. Если в строке i есть единичные элементы, то они выделяются вместе с соответствующим столбцом и одноименной строкой, не выделенные элементы записываются матрицу В.
Пример:
Рассмотрим сигнал f12 так как в матрице приема-сигнала (А), на пересечении строки 1 и столбца 2 имеется единица). Заполним матрицу взаимных сигналов (B) и заполним строку f12. Выделим на матрице А: строка 1, столбец 1, столбец 2, строку 2.

Выделяем из столбцов 1 и 2, строки единичных элементов.

На строке 1 матрицы «А» нет больше единичных элементов, значит запишем в матрицу В, в строку f12 на пересечении f43 столбца и f53 , единицу, в остальные пересечения строки f21 и остальных столбцов запишем ноль.

Выше изложенную операцию повторим для всех оставшихся сигналов и получим заполненную матрицу В.

Оптимизируем полученную матрицу взаимных сигналов, если, i–ая строка не содержит единицы, то выделяем, i –ую строку и i–ый столбец.
Пример:
Выделим столбцы и строки, в которых нет единиц.


Составим предварительные уравнения связи. Разобьём последующие действия на пункты.
1. Для каждой строки в оптимизированной матрице взаимных сигналов посчитаем ее вес, то есть сумму единиц, находящихся в строке, добавим в столбец оптимизированной матрицы приема и сигналов столбец «вес». Если все элементы имеют одинаковый вес равный количеству элементов минус 1, то предварительное уравнение связи будет состоять из всех элементов. Из матрицы выбираем строку fij и присваиваем ей приоритет 1. Удаляем столбцы, в которых данная строка fij имеет нули, удаляем строки, в которых столбец fij имеет нули, получим матрицу сигнала fij .
2. Оставшиеся строки сортируем от максимального веса к минимальному. Выбираем строку с наибольшим весом fke. Удаляем столбцы, в которых данная строка fke имеет нули, удаляем строки, в которых столбец fke имеет нули. Если строк с максимальным весом несколько, то необходимо узнать какие из них взаимодействуют между собой (для наилучшего результата выбирается максимальное количество связей), после этого разветвить данный шаг и вернуться к нему после выполнения пунктов 3. или 4. Такие строки в последующем будут считаться за одну, а столбцы (строки), в которых необходимо произвести удаление строк (столбцов), должны содержать хотя бы один ноль.
Если полученная строка имеет тот же вес, что и fij, то ей присваивается приоритет 2.
Пункт 1. выполняется до тех пор, пока в весах оставшихся строк есть максимальный элемент.
2. Анализируем оставшиеся строки (если таковых не осталось, то переходим к пункту 3.). Если их вес равен количеству строк, имеющих приоритет, необходимо записать в предварительное уравнение связи названия строк, имеющих приоритет 1 и 2, а также одну из оставшихся строк. Количество получившихся предварительных связей равно количеству строк, не имеющих приоритет. Далее пункт 3. пропускается.
3. Записываем в предварительное уравнение связи названия строк, имеющих приоритет 1 и 2, выписываем отдельно элементы с приоритетом 2.
4. Возвращаемся к оптимизированной матрице сигнала fij, удаляем в данной матрице стоки и столбцы, имеющие приоритет 2 (из пункта 2. или 3.) , если в оптимизированной матрице сигнала fij все элементы имеют вес равный 1 или в матрице остался только элемент fij, то переходим на пункт 8., иначе пункт 1.
Пример:
Добавим к матрице В, столбец «вес». Выберем на матрице В элемент f12, и построим оптимизированную матрицу f12, и присвоим f12 приоритет 1.

Уберем строки, которые на пересечении столбце равны f12 нулю, также уберем столбцы, на пересечении строки f12 равны нулю. Получим оптимизированную матрицу В f12.

Из оптимизированной матрицы f12, видим, что веса у f43 и f57 равны весу f12, присваиваем f43 и f57 приоритет 2

Выписываем отдельно элементы f43 и f57 . Выпишем уравнение связи с её весом ( f12, f43, f57) – 3. Из B f12 уберем строки и столбцы f43 и f57, получим.
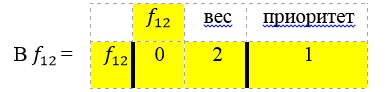
В матрице В f12 остался только 1 элемент, значит переходим к следующему элементу из матрице В. Применив алгоритм к остальным элементам получим уравнения связи с весами, и запишем общий список уравнений:
( ) – 3
) – 3
( f21, f57) – 2
( f23, f53) – 2
( f43, f12, f57) – 3
( f53, f12, f43) – 3
Распределяем частоты. Полученные уравнения частот сортируем по весам от максимума к минимуму. Принимаем уравнение с максимальным весом и записываем элементы уравнения с максимальным весом, в отдельную строку С, а принимаемое уравнение запишем в список принимаемых уравнений, из общего списка уравнений выделяем принимаемое уравнение. Исключим элементы, совпадавшие из строки С, во всех уравнениях связи если уравнение связи получилось с весом 1, то оно тоже выделяется из общего списка, повторим пункт 8. с начала, до тех пор пока общий список будет пустым. Получаем список принятых уравнений, именно сигналы отдельных уравнений могут находиться на одних и тех же частотах, обозначим каждое уравнение как  (
( ) и будем называть группой одночастотных сигналов, где
) и будем называть группой одночастотных сигналов, где  – обозначение уравнения, (
– обозначение уравнения, ( ) – состав группы одночастотных сигналов. Остальные сигналы, не вошедшие в список принятых уравнений, должны находиться на разных частотах.
) – состав группы одночастотных сигналов. Остальные сигналы, не вошедшие в список принятых уравнений, должны находиться на разных частотах.
Пример:
Общий список уравнений, отсортированный по весам от максимума к минимуму:
( ) – 3
) – 3
(f43, f12, f57 ) – 3
( f53, f12, f43) – 3
( f21, f57 ) – 2
( f23, f53) – 2
Примем ( ) – 3 и выпишем в строку С = (
) – 3 и выпишем в строку С = (  ), (
), (  ) – 3 вычеркнем из общего списка уравнений , вычеркнем элементы из С = (
) – 3 вычеркнем из общего списка уравнений , вычеркнем элементы из С = (  ), во всех оставшихся уравнений связи:
), во всех оставшихся уравнений связи:
(f21 ) – 1
(f23 ) – 1
Так как общий список уравнений имеет уравнения связи с весом равный 1, то эти уравнения вычеркиваются, следовательно, получаем пустой список.
Приходим к выводу, что группа сигналов  могут находиться на одних и тех же частотах и обозначим μ1(
могут находиться на одних и тех же частотах и обозначим μ1( ), остальные сигналы на разных частотах.
), остальные сигналы на разных частотах.
Распределим диапазон частот для каждого сигнала. Пусть ∆F будет равна разнице между верхней и нижней границей выделенного диапазона частот, и равна минимальному частотному диапазону. Для максимального распределения частот, рассмотрим два случая:
Отсутствие групп одночастотных сигналов:
так как все сигналы не могут находиться на одних и тех же частотах, то при распределении частот, сумма всех частот сигналов не может превышать выделенного диапазона частот, поэтому ∆F делим на количество сигналов и распределяем в пределах полученного значения (d).
Для первой частоты присваиваем левую границу частот, равную минимальной границе выделенного частотного диапазона, а правую границу, ставим равную левой плюс шаг равный d минус q (частотная проставка, не равная нулю). Для последующих частот левая граница равна левой границе предыдущей рассмотренной частоты плюс шаг d, а правая – левой границе рассматриваемой частоты плюс шаг равный d минус q.
- Наличие групп одночастотных сигналов:
Шаг 1. Вычитаем из ∆F величину, равную произведению количества частот, которые входят в группы, и ε. Полученное значение (f’) будем распределять между оставшимися частотами. Среди групп одночастотных сигналов выбирается (ются) та (те), которая (ые) имеет (ют) наибольшее число частот, входящих в нее (них). Из значения f’ вычитаем величину, равную произведению количества оставшихся (не максимальных) групп и ε. Полученное значение (f’’) будем распределять между группами сигналов, имеющими максимальное количество частот, входящих в них. Для этого разделим f’’ на количество максимальных групп. Полученная величина (f’’’).
Шаг 2. Для первой частоты (частотам первой группы) присваиваем левую границу частот, равную минимальной границе выделенного частотного диапазона, а правую границу, ставим равную левой плюс шаг равный d* минус q (частотная проставка, не равная нулю). Для последующих частот (частот других групп) левая граница равна левой границе предыдущей рассмотренной частоты плюс шаг d*, а правая – левой границе рассматриваемой частоты плюс шаг равный d* минус q.
Шаг d* для частот групп, имеющих максимальное количество частот, равен f’’’. Для оставшихся частот, d* равен ε.
Пример:
Так как F ∊ [3500..3611] МГц и минимальный частотный диапазон сигнала 1 МГц, то ∆F = 111 МГц . Количество сигналов равно 14, так как есть сигналы, которые м огут находиться на одном и том частотном диапазоне, и таких сигналов у нас 3, то объединяем их в единое и сумма сигналов получается 10 уникальных плюс одно объединение. Распределим уникальные частотные диапазоны сигналов: S =  МГц. Распределим S = 100 МГц объединенных сигналов для частотного диапазона, так как объединений у нас одно, то 100 МГц приходится на объединение сигналов, в результате,
МГц. Распределим S = 100 МГц объединенных сигналов для частотного диапазона, так как объединений у нас одно, то 100 МГц приходится на объединение сигналов, в результате,  = 100 МГц, получим:
= 100 МГц, получим:

МГц
 = 100
= 100
Распределим диапазоны частот.
 МГц
МГц
 МГц
МГц
 МГц
МГц
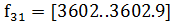 МГц
МГц
 МГц
МГц
 МГц
МГц
 МГц
МГц
 МГц
МГц
 МГц
МГц
 МГц
МГц
 МГц
МГц
 МГц
МГц
Рассматриваемый пример был смоделирован в среде WiMAP-4G, результат модулирования представлен на рисунке 2.

Рисунок 2. Результат моделирования исследования Mesh сетей.
На Рисунке 2 представлено изображение уровней сигналов, где синим цветом обозначен, наилучший сигнал, что говорит о правильном частотном распределении.
Вывод
В данной статье был разработан алгоритм распределения частотного диапазона, и справедливость алгоритма подтверждается моделью Mesh-сети, созданной в среде WiMAP-4G.
Стоит отметить, что алгоритм максимально полно находит количество сигналов, которые могут находиться на одних и тех же частотах, тем самым это дает наиболее рациональное использование выделенного диапазона частот. В процессе работы алгоритма осуществляется оптимизация матрицы приема передачи, это дает возможность исключения изолированных радиостанций, что влечет к уменьшенью времени работы алгоритма, также в ходе работы производится оптимизация матрицы взаимных сигналов, что также дает сокращение времени работы алгоритма.
Рассматриваемый алгоритм оптимален для небольшого количества радиостанций (около 50). Увеличение числа радиостанций влечет за собой увеличению затрачиваемого времени на работу алгоритма. Данный недочет находится в стадии разработки.
Список литературы:
- Альшаев И.А., Лаврухин В.А.. О ПРОЕКТИРОВАНИИ И ОПТИМИЗАЦИИ СЕТЕЙ WI-FI // Информационные технологии и телекоммуникации. 2016. Том 4. № 1. С. 87–95.
- Гаркуша С. В. Анализ результатов распределения частотных каналов в многоканальных многоинтерфейсных mesh-сетях стандарта IEEE 802.11 // Сборник научных трудов «Цифровые технологи». – 2011 – №10 – с. 51 – 62.
- Гаркуша С.В. Иерархическо-координационный метод распределения частотных каналов mesh-сети IEEE 802.11 на основе принципа прогнозирования взаимодействий // Управление, вычислительная техника и информатика. – 2014 – c. 156 – 166.
- Гаркуша C.В. Модель сбалансированного распределения подканалов в mesh-сети, использующей технологию WiMax // Инфокоммуникационные системы. – 2013 – c. 135–140.
- Лемешко А. В. Модель распределения частотных каналов с учетом территориальной удаленности станций в многоканальных mesh-сетях // Збірник наукових праць Харківського університету Повітряних Сил. – 2009 – № 22 – с. 38 – 41.
- Лемешко A.В. Разработка и анализ двухиндексной модели распределения каналов в многоканальной mesh-сети стандарта IEEE 802.11 // Электронное научное специализированное издание – журнал «Проблемы телекоммуникаций». – 2011 – c. 38–60.
дипломов


Оставить комментарий