Проект ракеты-носителя «Феникс» с четырьмя ускорителями типа универсальный ракетный модуль - 1

Введение

Одним из выдающихся достижений отечественной ракетно-космической промышленности по праву считается создание ракето-носителя (РН) «Зенит». Эта ракета, опередившая свое время, имеющая высокоавтоматизированную пусковую установку, стартовала более 50 раз, вывела множество космических аппаратов на различные орбиты и использовалась на перспективном стартовом комплексе «Морской старт». На сегодняшний день дальнейшая эксплуатация РН «Зенит» не представляется возможной. В связи с этим предлагается проект РН «Феникс» на основе космического ракетного комплекса «Зенит» с более широкими возможностями вывода полезной нагрузки благодаря установке боковых ускорителей («Феникс» - кодовое название серии научно-исследовательских работ с выходом на конструкторский и лётные космические испытания к 2025 году).

Центральный блок останется без изменений и будет представлять из себя первую ступень РН «Зенит».  В качестве бокового блока будет выступать боковой блок типа универсальный ракетный модуль -1 (УРМ-1) (рисунок - 2), устанавливаемый на РН семейства «Ангара». Конструктивно-компоновочная схема (ККС) изображена на рисунке 1.

Рисунок 1 - ККС РН «Феникс» с ускорителями. 1 – ракета-носитель, 2 – четыре ускорителя типа УРМ-1.

Доработки ракеты сводятся к установке узлов крепления на силовых шпангоутах на первой ступени носителя, а также к усилению шпангоутов. Сверху ускоритель закрывается ненесущим носовым обтекателем.

Рисунок 2- Универсальный ракетный модуль - 1 – ЖРД РД-191, 2 –бак горючего, 3 – бак окислителя, 4 – головной обтекатель УРМ.

Для снижения тепловой и газодинамической нагрузки на хвостовую часть РН ускоритель крепится так, чтобы его сопло было на одном уровне с соплами маршевого двигателя.

Для запуска РН «Феникс» с существующего стартового стола РН «Зенит», не содержащего дополнительных газоводов и не позволяющего включать ускорители на старте, ракета взлетает на основных маршевых ЖРД, тяга которых форсируется на 5%. Ускорители включаются позже, на безопасной высоте – около 50-80 м от земли, спустя примерно 7-8 с после «контакта подъема».

Для осуществления проекта предполагается оставить без изменений:

-общую конфигурацию первой ступени РН «Зенит»;

-общую конструкцию ступеней;

-космическую головную часть;

-конструкцию пускового стола;

-технологическое оборудование монтажно-испытательного корпуса.

Для реализации проекта необходимо предусмотреть следующие изменения конструкции ракеты-носителя, системы управления, стартового комплекса и технологии подготовки к пуску:

         - при подвеске четырех ускорителей с их размещением между баками горючего первой ступени необходимы доработки первой ступени ракеты;

- в системе управления необходимо предусмотреть гибкое изменение траектории выведения РН с использованием системы управления с бортовой цифровой вычислительной машины (БЦВМ) и с учетом ускорителей, с тем, чтобы решать задачу попадания отбрасываемых элементов ракеты вместе с ускорителями в существующие поля падения.

-для подвешивания ускорителей и транспортировки РН с ускорителями на транспортно-установочном агрегате он должен быть переоборудован.

Расчет прироста скорости РН с установленными боковыми ускорителями

Произведем расчет прироста скорости с четырьмя ускорителями УРМ -1, использую методику приближенного расчета скорости [3]. Для этого необходимо вычислить скорость РН с установленными на нем ускорителями и без таковых. Характеристики ускорителя УРМ-1 и установленного на нем жидкостного ракетного двигателя (ЖРД) РД-191, необходимые для расчета, представлены в таблице 1 и 2 соответственно.

Таблица 1 – Характеристики УРМ-1

Таблица 2 –Характеристики ЖРД РД-191

  Прирост скорости находим по формуле: Δv = v_уск  - v,

  где v_уск  - скорость РН в момент отделения первой ступени и ускорителей; v – скорость РН без ускорителей в момент отделения первой ступени.    Определим скорость РН с ускорителями [1]:

  v_уск = v _{ц уск} - Δv _{гр уск}   - Δv _{ад уск} - Δv _{р уск},

  где v _{ц уск} – идеальная скорость, определяемая по формуле Циолковского;

Δv _{гр. уск} - потери скорости на преодоление гравитационного сопротивления Земли; Δv _{ад уск} – потери скорости на преодоление аэродинамического сопротивления; Δv _{р уск}  - потери скорости из-за снижения величины тяги двигателя, работающего при атмосферном давлении (определяются по графику на рис. 3).

Рисунок 3 – Эмпирические зависимости коэффициентов K_gg, Δv_p, K_g и K_d для расчета скорости РН

Находим идеальную скорость РН с ускорителями по формуле Циолковского:

  v_{ц уск} = Р_уд · g ln (1 + m_т/ m_сух),

  где Р_уд – удельная тяга ЖРД ракеты-носителя с ускорителями; m_т – масса жидкого топлива в первой ступени и в УРМ; m_сух - сухая масса первой ступени РН в конце ее работы.

  Р_уд = Р_жрд  + Р_уск / G_жрд + G_уск

где G_жрд = m_{т ж} / t_{1 ст} , m_{т ж} – масса жидкого топлива первой ступени РН «Зенит», m_{т ж}  = 349906 кг, t_{1 ст} – время работы двигателя первой ступени РН, t_{1 ст} = 140 с.

  G_жрд = 349906/ 140 = 2320 кг/с.

  G_уск = Р_уск / I_уск = 1923000 / 3048 = 630 кг/с.

  Р_уд = 7254000 + 1923000 / 2320 + 630 = 3090 м/с или 315 с.

Находим массу топлива первой ступени РН и УРМ:

  m_т = 349906 + 127000 = 476906 кг.

Находим сухую массу первой ступени РН, УРМ и второй ступени РН:

  m _сух  = 27940 + 8000 + 89800 = 125740 кг;

Находим идеальную скорость РН с ускорителями:

  v_{ц уск} = 315 9,81 ln (1 + 476906 / 125740) = 4839 м/с.

Находим гравитационные потери скорости для РН с ускорителями:

  Δv _{гр уск}   = (g t_к - K_gg)[1 – K_g (1- m_сух/m₀)(θ⁰_к/90⁰)²]

  где t_к – полное время работы двигателей первой ступени РН и УРМ, t_к = 140 с; K_gg определяем по графику на рис. 3, при этом учитываем, что удельная тяга в пустоте ЖРД РН и УРМ Р_{уд п уск} = 343 с, из графика K_gg = 45. K_g определяем по графику на рис. 3 [1], при этом учитываем, что стартовая масса РН с УРМ m_{0 уск} = 594000 кг, m_{сух уск} = m_{сух 1 ст}  + m_{сух УРМ}  + m_{0 2 ст} = 27940 + 8000 + 89800 = 125740 кг, m_{0 уск} / m_{сух уск} = 4,7. Кроме того, находим отношение Р_уск / m_{0 уск} = 940978 кгс/ 594000 кг = 1,6.

С учетом вышеизложенного K_g = 0,7. Принимаем, что угол наклона вектора скорости ракеты в конце работы первой ступени θ_к° = 60°. Находим Δν_{гр уск} :

  Δν_гр = (9,81 · 140 - 48)[1 - 0,7(1- 35940 / 594000)()²] = 936 м/с.

Находим Δv _{ад уск} – потери скорости на преодоление аэродинамического сопротивления:

  Δν_ад =

Где К_d = 0,1 (по графику рис. 3, с учетом данных таблицы формул и исходных данных) [1]; C_{х уск} – коэффициент аэродинамического сопротивления РН с УРМ, конструкция которой состоит из конуса с углом полураствора θ = 20°, цилиндра диаметром 3,9 м, четырех усеченных конусов УРМ с углом полураствора θ = 30°, четырех цилиндров диаметром 2,9 м, для сверхзвуковой скорости [8]:

  C_{х уск} = C_{х кон РН} + C_{х цил РН} + C_{х кон УРМ} + C_{х цил УРМ},

  где: C_{х цил РН и} C_{х цил УРМ} = 0 при угле атаки, равном 0⁰;

  C_{х кон РН} = 2 · sin² θ _{кон РН} + 2 · 4 · sin² θ_{кон УРМ} = 2 · sin² 20° + 8 · sin² 30° = 2,234.

S_м – площадь миделя первой ступени с четырьмя УРМ диаметром 2,9 м:

S_м = π · 4 · d²_УРМ /4 = 3,14 · 2,9² = 21,04 м².

  Δν_{ад УРМ} = 0,1 · 2,234 · 21,04 / 594000 = 7,9 · 10^-6 м/с.

Находим Δν_р – потери скорости из-за снижения тяги двигателя, работающего при атмосферном давлении. из графика рис. 3, с учетом данных из таблицы формул Δν _{р уск} = 80 м/с.

Находим Δν _уск = 4839 – 936 – 80 - 7,9 · 10^-6 = 7201 м/с.

Расчет скорости РН без ускорителей

Определим скорость РН без ускорителей [1]:

  v = v _ц  - Δv _гр - Δv _ад  - Δv _р,

где  v _ц  – идеальная скорость, определяемая по формуле Циолковского; Δv_гр - потери скорости на преодоление гравитационного сопротивления Земли; Δv_ад – потери скорости на преодоление аэродинамического сопротивления; Δv _р - потери скорости из-за снижения величины тяги двигателя, работающего при атмосферном давлении (определяются по графику на рис. 3).

Находим идеальную скорость РН с ускорителями по формуле Циолковского:

  v_ц  = Р_уд · g · ln (1 + m_т/ m_сух),

где Р_уд – удельная тяга ЖРД ракеты-носителя; m_т – масса жидкого топлива в первой ступени; m_сух  - сухая масса первой ступени РН и заправленной второй ступени.

Масса топлива первой ступени РН:

  m_т = 349906 кг.

Находим сухую массу первой ступени и заправленной второй ступени РН:

  m _сух  = 27940 + 89800 = 117740 кг;

Находим идеальную скорость РН с ускорителями:

  v_ц = 308 · 9,81 · ln (1 + 349906 / 117740) = 4163 м/с.

Находим гравитационные потери скорости для РН:

  Δv _гр   = (g · t_к - K_gg) · [1 – K_g (1- m_сух/m₀) · (θ⁰_к/90⁰)²],

  где t_к – полное время работы двигателей первой ступени РН, t_к = 140 с;

K_gg определяем по графику на рис. 3, при этом учитываем, что удельная тяга в пустоте ЖРД РН Р_{уд п}  = 336 с, из графика K_gg = 46. K_g определяем по графику на рис. 3, при этом учитываем, что стартовая масса РН:

  m₀  = 459000 кг, m_сух  = m_{сух 1 ст}  + m_{0 2 ст} = 27940 + 89800 = 117740 кг.

Кроме того, находим отношение Р / m₀  = 1,6.

С учетом вышеизложенного K_g = 0,78.

Принимаем, что угол наклона вектора скорости ракеты в конце работы первой ступени θ_к° = 60°.

Находим Δν_гр :

  Δν_гр = (9,81 · 140 - 46) · [1 - 0,78 · (1- 117740 / 459000) · ( )²] = 1039 м/с.

Находим Δv _ад – потери скорости на преодоление аэродинамического сопротивления:

  Δν_ад =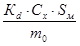

  где К_d = 0,1 (по графику рис. 3, с учетом данных таблицы формул и исходных данных) [1]; C_{х уск} – коэффициент аэродинамического сопротивления РН, конструкция которой состоит из конуса с углом полураствора θ = 20°, цилиндра диаметром 3,9 м для сверхзвуковой скорости [8]:

  C_х  = C_{х кон РН} + C_{х цил РН} ,

  где  C_{х цил РН} = 0 при угле атаки, равном 0⁰;

  C_{х кон РН}  = 2 · sin² θ _{кон РН} = 2 · sin² 20°  = 0,234.

  S_м – площадь миделя первой ступени диаметром 3,9 м:

  S_м = π · d² /4 = 3,14 · 3,9² = 11,94 м².

  Δν_ад  = 0,1 · 0,234 · 11,94 / 459000 = 6,1 · 10^-5 м/с.

Находим Δν_р – потери скорости из-за снижения тяги двигателя, работающего при атмосферном давлении. из графика рис. 3, Δν _{р уск} = 60 м/с.

  Находим Δν  = 4163 – 1039 – 60 - 6,1 · 10^-5 = 3064 м/с.

  Δν = 3823 – 3064 = 759 м/с.

Вывод: Достигается увеличение скорости РН с ускорителями типа УРМ-1 на 759 м/с. Прирост скорости повысит массу выводимой полезной нагрузки (для низкой околоземной орбиты с 13 тонн до 25 тонн) без модификаций второй ступени и разгонного блока.

Расчет на прочность шпангоутов крепления ускорителей к РН

Схема верхнего узла связи ускорителя и первой ступени РН «Зенит» показана на рис.4 [2].

Рисунок 4 – Схема верхнего узла связи центрального блока с УРМ-1

(1-балка коробчатого типа; 2 – кронштейн; 3 – сечение балки; 4 – Шпангоут таврового типа)

Торцевые (стыковочные) шпангоуты, расположенные в стыке двух отсеков, нагружены сосредоточенными силами, возникающими в стыковых болтах от растяжения и изгиба. Усиленные (силовые) шпангоуты воспринимают сосредоточенные силы в узлах подвески баков и грузов от инерционных осевых сил, а в узлах подвески ЖРД – от тяги двигателя. В общем случае на шпангоут действуют следующие внешние нагрузки, приложенные перпендикулярно его плоскости (рис.4): осевая сила P, изгибающий момент L, крутящий момент K, погонный крутящий момент M_кр.п., которые уравновешиваются погонными усилиями q.

При действии внешних нагрузок в сечении кольца возникают внутренние усилия: поперечная сила Q, изгибающий момент M_и, крутящий момент M_кр. Зная внутренние усилия Q, M_кр, M_и, можно определить касательные и нормальные напряжения по формулам:

  ; ; ;

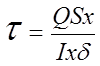  где S_x – статистический момент отсеченной части сечения; I_x – момент инерции сечения; W_кр – момент сопротивления сечения при кручении; y – расстояние от нейтральной оси до произвольной точки сечения.

При действии равномерно распределенного погонного крутящего момента в сечении шпангоута возникают нормальные напряжения (рис.5):

  ,

  где M_кр.п.  - равномерно распределенный по шпангоуту погонный крутящий момент;

  r – радиус до центра масс сечения шпангоута (рис.5).

Рисунок 5 - Схема нагружения шпангоута внешними нагрузками, приложенными перпендикулярно его плоскости

Рисунок 6 - Схема нагружения шпангоута равномерно распределенным погонным крутящим моментом M_кр.п.,  эпюра нормальных напряжений в сечении

Из формулы для расчета касательных напряжений:

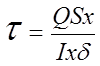
находим ,

где σ =[σ]*n, принимаем коэффициент запаса прочности n=1,5, [σ]=150 МПа (для дюралюминия), σ=150*10⁶  *1,5=225*10⁶ Па;

r-радиус шпангоута, r=1,95 м.

y=0,1 м, где тяга четырех ускорителей P_уск=196224 кгс=1923000 Н, x=0,03м.

М _{кр. п.} = = =4710,926 Н.

=4,082*10^-6 м⁴.

Из формулы для расчета момента инерции прямоугольного сечения шпангоута находим уточненную величину y:

4,082*10^-6м⁴, откуда:  0,113 м

Шпангоут должен иметь высоту сечения 2*0,113=0,226 м и ширину сечения 2*0,03=0,06 м.

Для сравнения нормальных и касательных напряжений для выбранного сечения шпангоута находим касательные напряжения:

от действия поперечной силы ,

где Q-тяга от четырех ускорителей, Q=1923000 Н,

I_x=3,641*10^-6 м⁴, δ=0,06 м, находим S_x-статический момент отсеченной части сечения, в данном случае S_x=0, таким образом касательные напряжения равны нулю.

Находим касательные напряжения от крутящего момента:

где M_кр =P_уск1*x= 480750*0,03=14422,5 Нм.

W_кр- момент сопротивления сечения при кручении, W_кр=β*b³,

где находим β из таблицы 6.1 [2] в зависимости от соотношения сторон прямоугольного сечения шпангоута.

β=1,1. b = 0,06 м.

W_кр=1,1*(0,06)³=0,0002376 м³.

60,700 МПа.

Вывод: Касательные напряжения при кручении меньше допускаемых, что удовлетворяет условиям прочности, как следствие нет необходимости вносить изменения в конструкцию центрального блока.

Заключение

В данной работе в первом приближении разработан проект ракеты-носителя «Феникс» с четырьмя ускорителями типа УРМ на первой ступени. Результаты расчета показали, что проектирование РН «Феникс» с четырьмя ускорителями типа универсальный ракетный модуль - 1 является выполнимой задачей, при минимальных затратах и изменениях в ракето-космическом комплексе «Зенит». Данный РН может стать экологически безопасной и технологически более совершенной заменой нынешнему РН тяжелого класса «Протон-М», с варьируемой в широком диапазоне полезной нагрузкой.

Список литературы:

1. Добровольский  М.В.  Жидкостные  ракетные  двигатели:  учеб.  для  вузов.  –  М.:  МГТУ  имени  Н.Э.  Баумана,  2006.  –  269  с.

2. Паничкин Н.И., Слепушкин Ю.В. Конструкция и проектирование летательных аппаратов: - М.: Машиностроение, 1985.

3. Солодов. А.В. Инженерный справочник по космической технике: учеб. для вузов. - М.: Воениздат, 1977.

4. Уманский С.П.  Ракеты-  носители.  Космодромы: учеб.  для вузов.  –  М.:  Рестарт, 2001.  –  172 c.

7. Шустов И.Г. Двигатели 1944-2000: авиационные, ракетные, морские, наземные. – М.: ООО АКС-Конверсалт, 2000.

8. Щебуняев, Е.Ф., Юрьев, А.С. Аэродинамика летательных аппаратов: -учебное пособие. -  М.: Министерство обороны СССР, 1978.